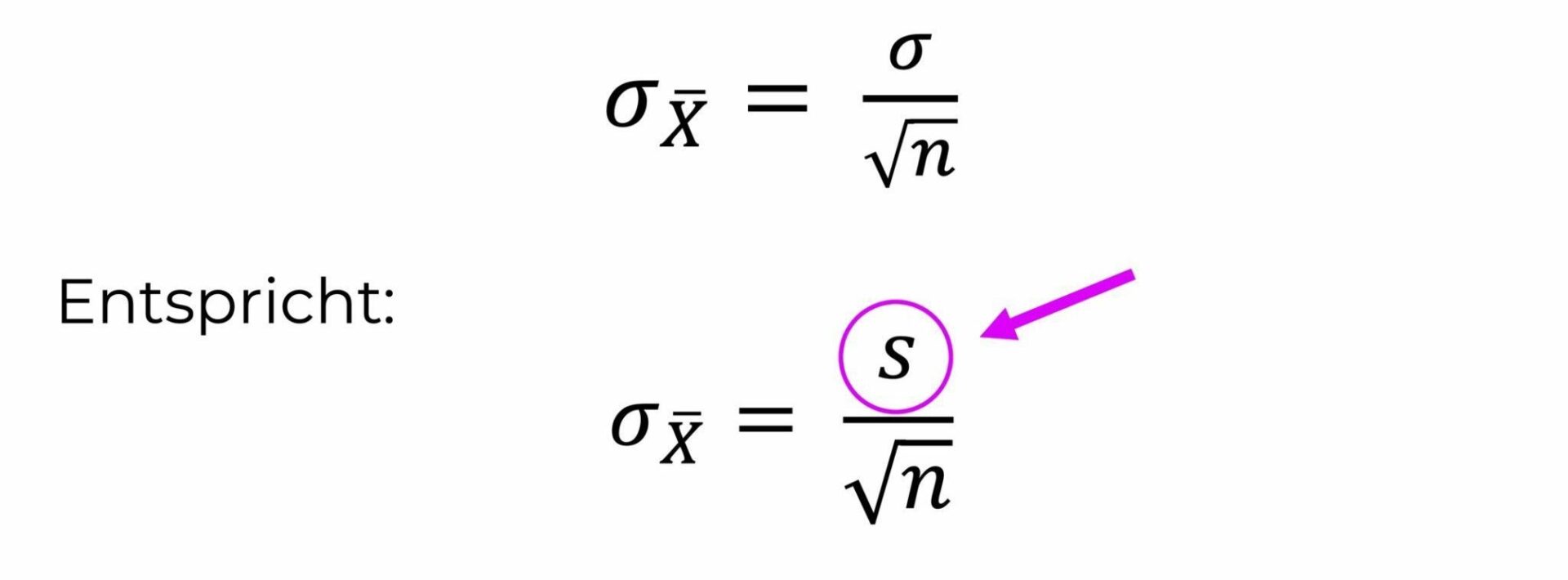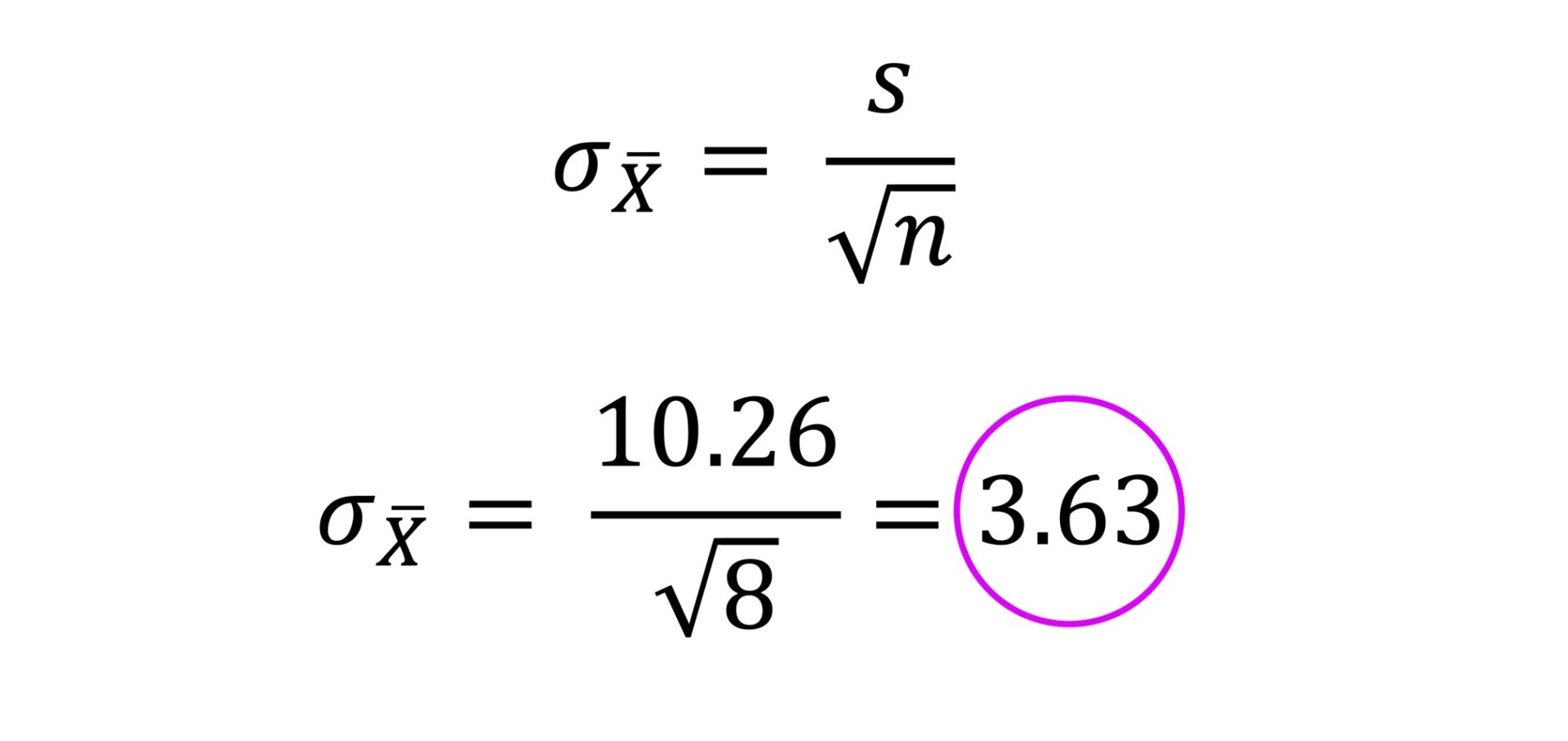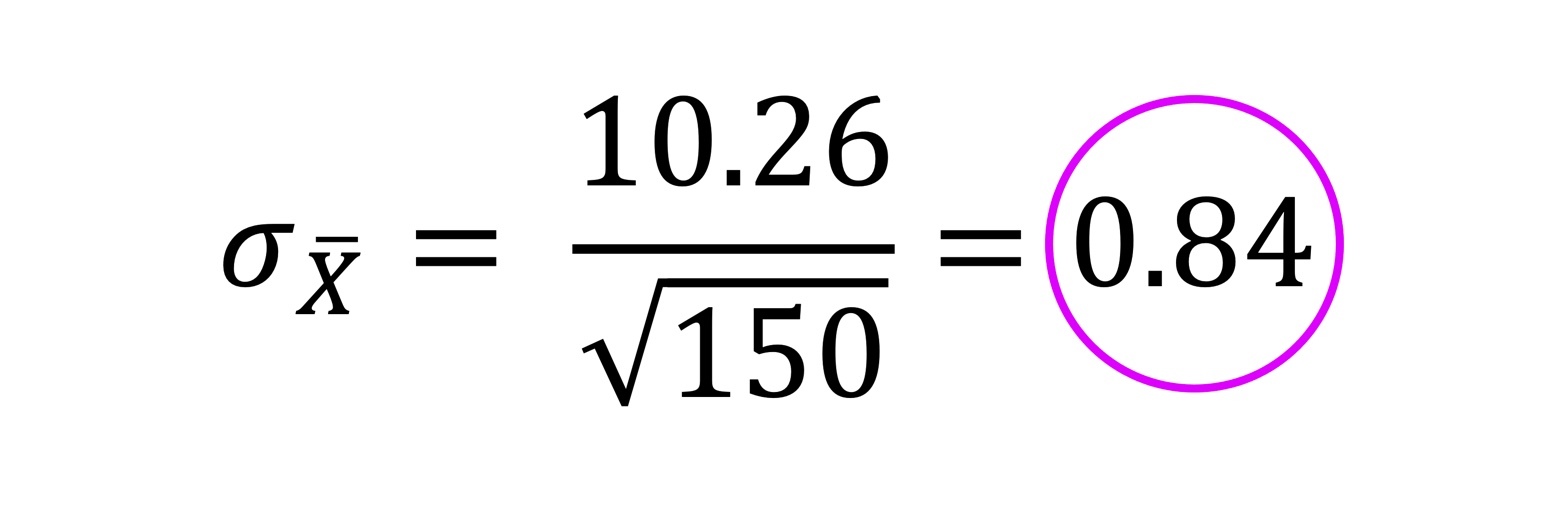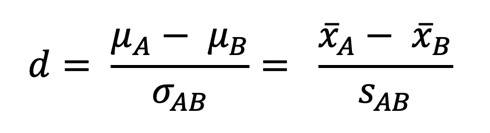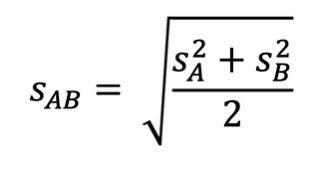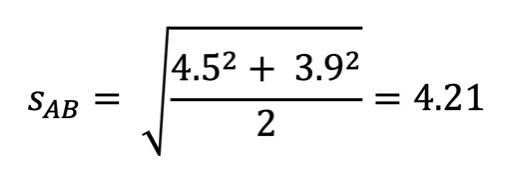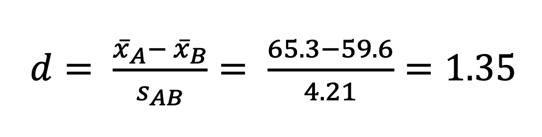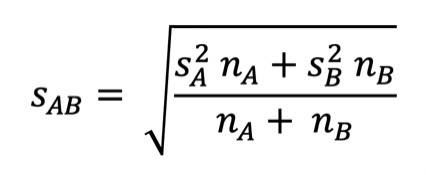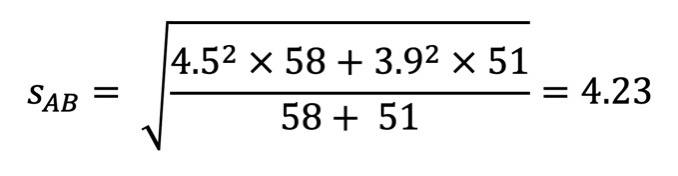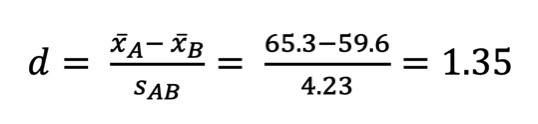Schließende Statistik leicht gemacht! Archive

Category Archives for Schließende Statistik leicht gemacht!

Einstichproben-t-Test einfach erklärt!

Der t-Tests gibt es ja viele, so dass gerne ein wenig Verwirrung aufkommt, wann man welchen verwendet.

Daher erhältst du in diesem Blog Post das rundum sorglos Paket zum Einstichproben-t-Test, auch t-Test für eine Stichprobe genannt.

Ich erzähle dir, worum es dabei geht, wann du ihn verwendest, wie er berechnet und interpretiert wird! Da kann dann t-Test-technisch nicht mehr allzu viel schiefgehen...

Und wenn du dazu und zu vielen bunten weiteren Tests Videos sehen möchtest, ist mein Videokurs zur Inferenzstatistik genau das Richtige für dich!

Allgemeines zum Thema t-Tests erfährst du hier.

Inhaltsverzeichnis

Worum geht's beim Einstichproben-t-Test &

in welchen Bereich der Statistik gehört er?

Beispiel

Wie du den Einstichproben-t-Test erkennst

Voraussetzungen & nonparametrische Alternative

Das Grundprinzip – einfach erklärt

Vorgehen bei der händischen Berechnung

Welche Hypothesen aufgestellt werden können

Hypothesen für unser Beispiel

Wo wir hinwollen:

Formel für den Einstichproben-t-Test

Ergebnis korrekt berichten

Interpretation für Tante Erna

Kurz & knackig zusammengefasst

Worum geht's beim Einstichproben-t-Test &

in welchen Bereich der Statistik gehört er?

WORUM ES GEHT

Um den Unterschied zwischen einem in der Population vermuteten oder bereits bekannten Mittelwert und dem Mittelwert einer neu erhobenen Stichprobe.

WOFÜR MAN IHN BRAUCHT

Vorwiegend für die Klausur, denn in der Praxis kommt dieser Test eher selten zum Einsatz...

Wie erwähnt, wird entweder ein bereits bekannter Mittelwert durch die Daten einer neuen Stichprobe herausgefordert oder aber es wird ein vermuteter Wert auf seinen „Wahrheitsgehalt" hin überprüft.

Der Einstichproben-t-Test (= t-Test für eine Stichprobe) ist eine der drei Varianten der t-Tests.

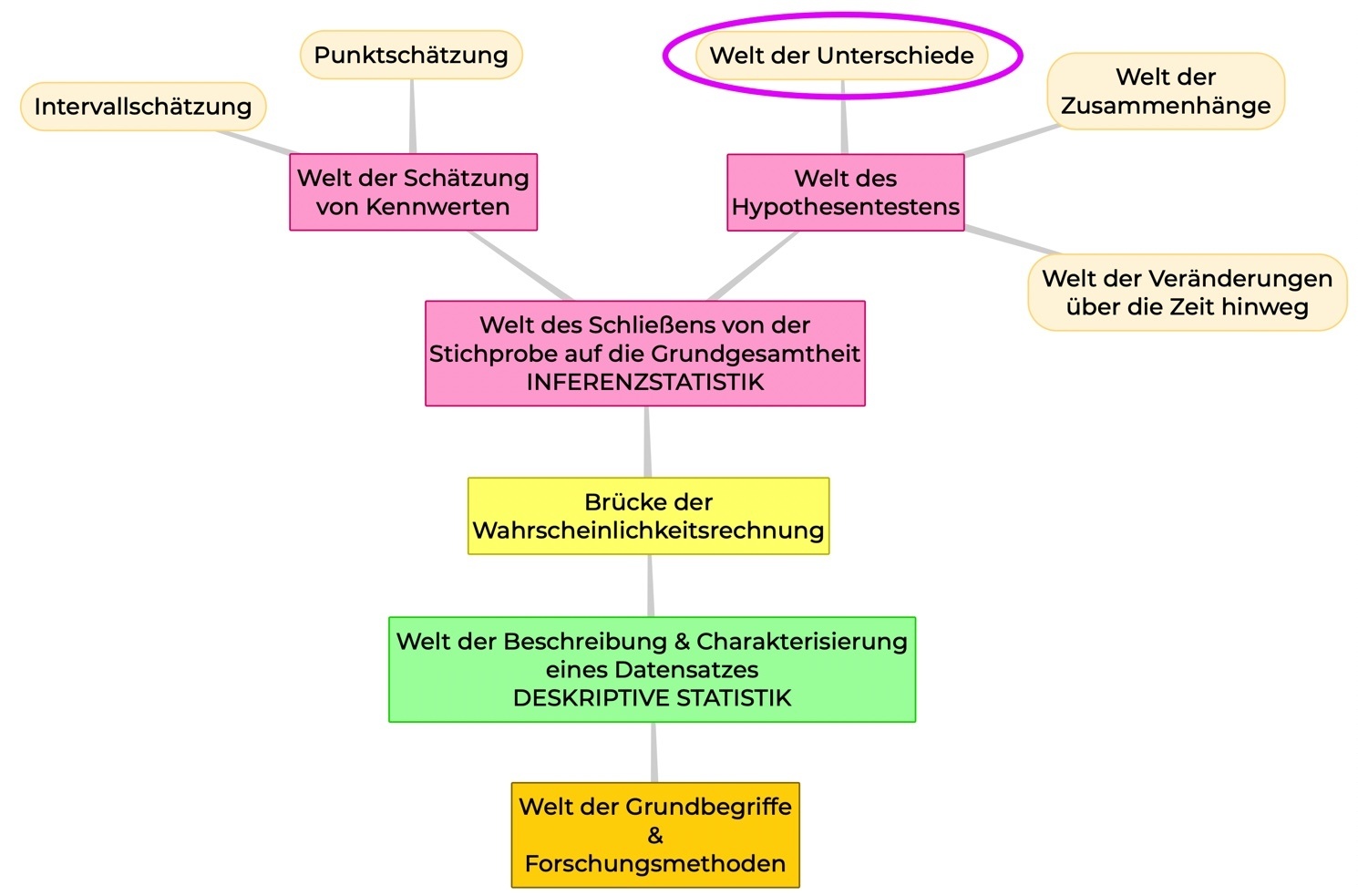
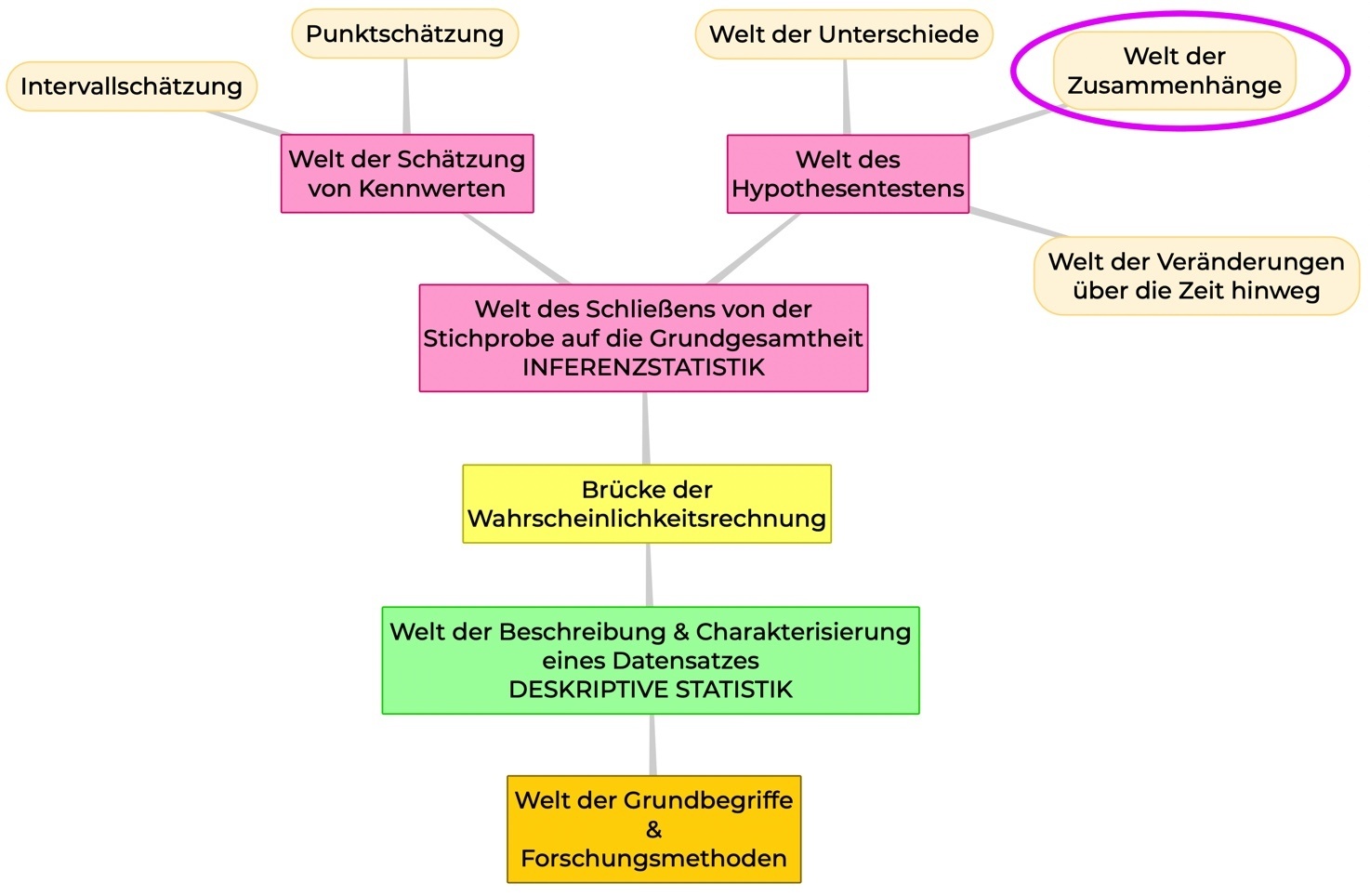
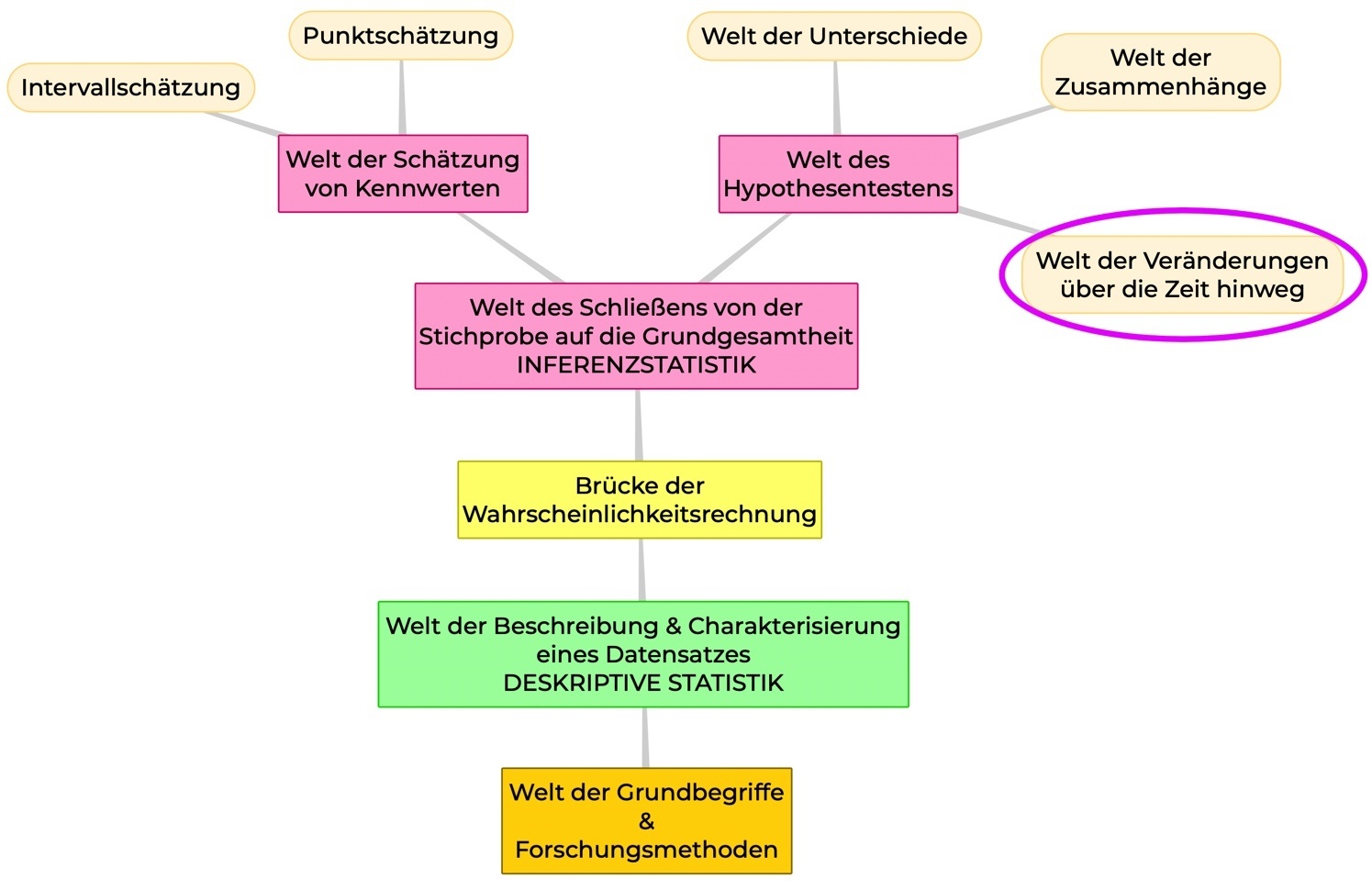
WO BEFINDEN WIR UNS?

In der Welt der Unterschiede, d. h. bei den Unterschiedshypothesen.

Beispiel

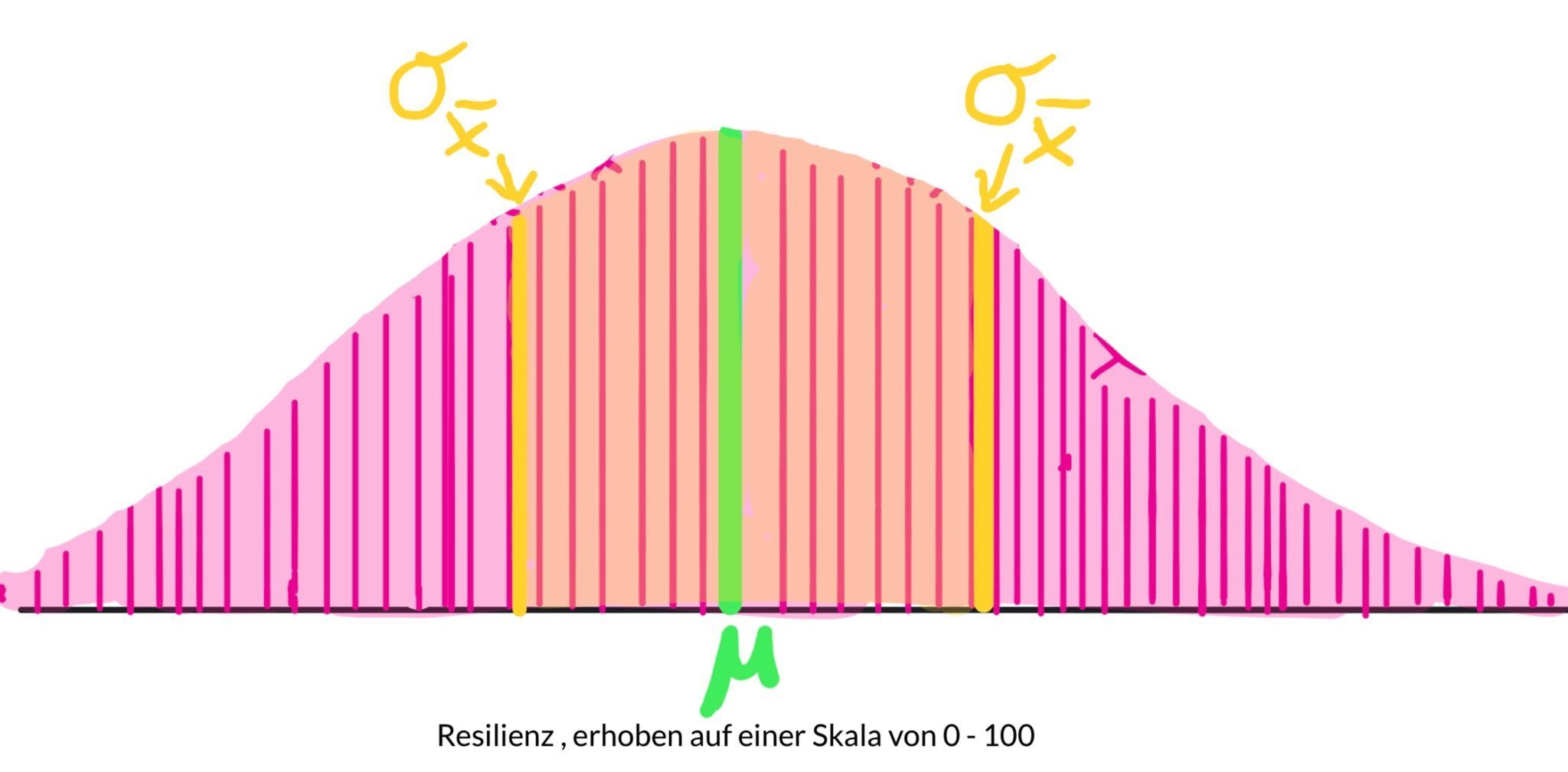
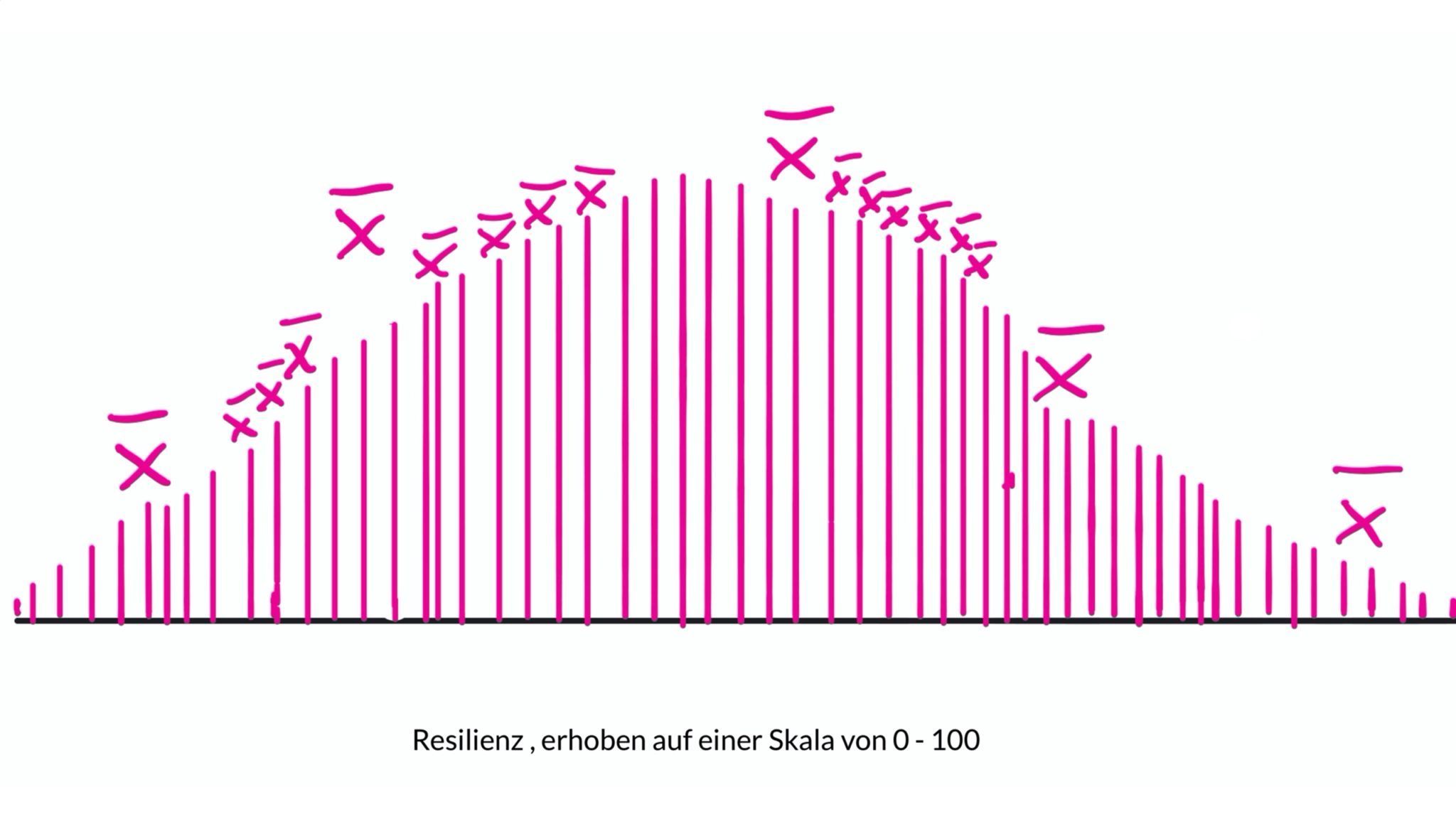
Du nimmst an, dass das durchschnittliche Glücksgefühl nach dem Urlaub (erhoben auf einer Skala von 0 – 100) signifikant von 50, dem „Mittelpunkt" der Skala, abweicht.

Nun schnappst du dir eine Stichprobe von 120 Reisenden und erhebst nach ihrer Rückkunft das Glücksgefühl.

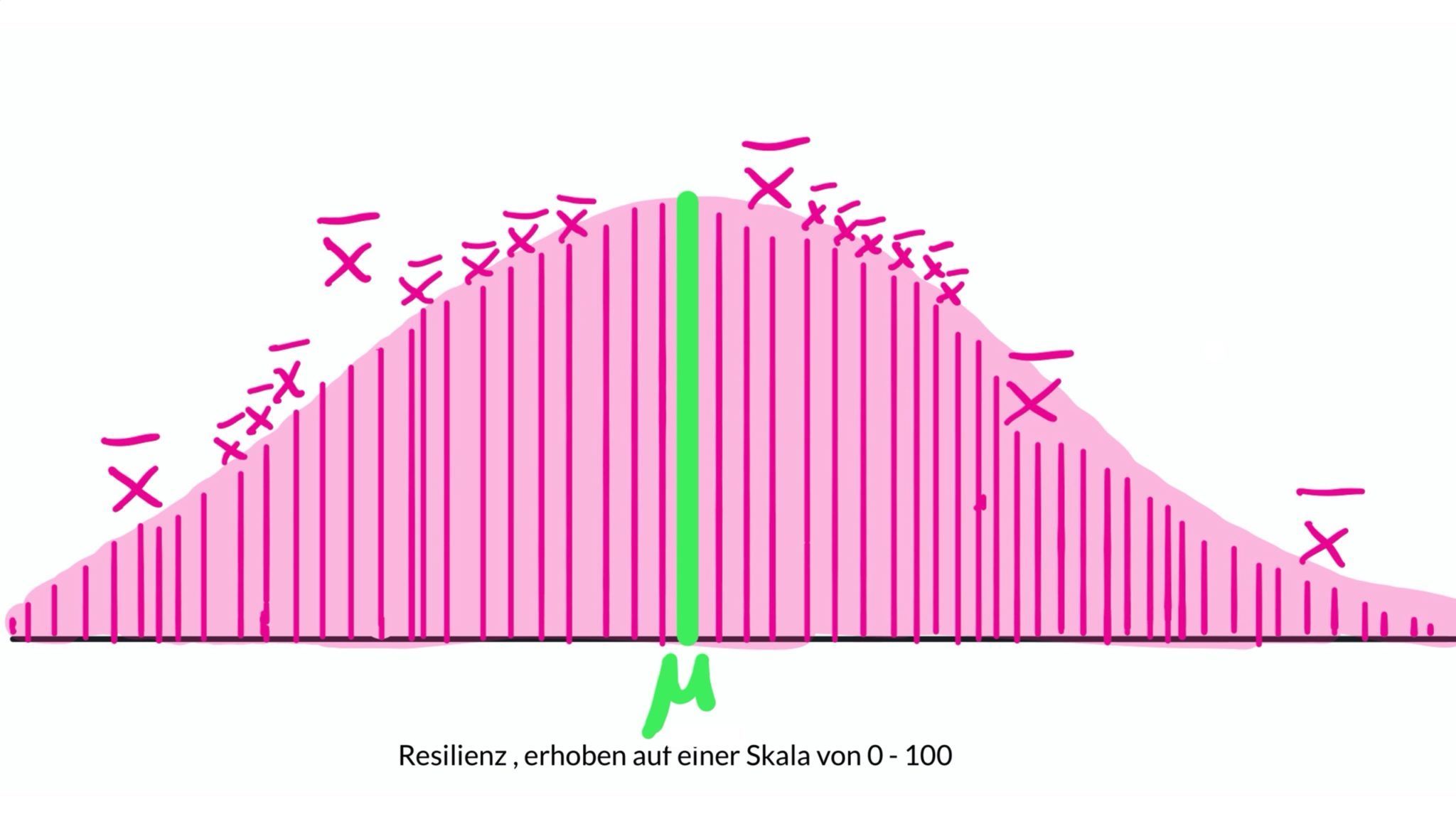
Aus diesen 120 Werten berechnest du einen Mittelwert und vergleichst diesen mit deinem angenommenen Mittel- bzw. Erwartungswert von 50: Liegt er bei 50 oder weicht er deutlich ab?

Du stellst also den Mittelwert aus deiner Stichprobe einem hypothetisch angenommenen (oder auch bekannten) Mittelwert bzw. Erwartungswert mü gegenüber.

DAMIT HABEN WIR:

- einen Unterschied zwischen einem angenommenen und einem aus den Daten EINER Stichprobe errechneten Mittelwert

- voneinander unabhängige Messungen

- 1 metrische normalverteilte AV (= abhängige Variable)

- 1 Messung (= nur ein Messzeitpunkt)

= die klassischen Anzeichen für einen Einstichproben-t-Test!

Wie du zu dieser Entscheidung kommst, siehst du hier:

Wie du den Einstichproben-t-Test erkennst

Das könnten HINWEIS-WÖRTER sein wie:

- „Es ist bekannt, dass die durchschnittliche Aufmerksamkeitsspanne bei Erwachsenen 4 Sekunden beträgt. Eine Forscherin zweifelt diese Annahme an und will untersuchen, ob die Aufmerksamkeitsspanne tatsächlich deutlich höher ist."

- Es geht also darum, dass etwas bereits bekannt ist oder ein bestimmter Wert vermutet und dann anhand einer Stichprobe überprüft wird.

- Deine AV ist metrisch und die Varianz bzw. Standardabweichung unbekannt. Ist die Varianz bzw. Standardabweichung bekannt, solltest du stattdessen den Einstichproben-Gauß-Test (= z-Test) verwenden!

- Es werden nur bei EINER Stichprobe Daten erhoben

TYPISCHE FRAGESTELLUNGEN

In einem Gedächtnistest werden durchschnittlich 32 Wörter erinnert. 10 Jahre nach Erscheinen des Tests soll dieser Wert erneut überprüft werden, denn es wird angenommen, dass die Anzahl der erinnerten Wörter von 32 abweicht. (Ungerichtete Hypothese)

Es ist bekannt, dass die durchschnittliche Abenteuerlust bei Käfigtauchenden auf einer Skala von 0 bis 100 bei 75 liegt. Wir vermuten, dass die Abenteuerlust jedoch tatsächlich höher liegt und überprüfen diese Annahme mit den Daten von 30 Käfigtauchenden. (Rechtsseitige Hypothese)

Voraussetzungen & nonparametrische Alternative

WELCHE VORAUSSETZUNGEN ERFÜLLT SEIN MÜSSEN

- Die AV ist metrisch und normalverteilt

- Die Varianz bzw. Standardabweichung ist nicht bekannt und muss aus den Daten der Stichprobe geschätzt werden

NONPARAMETRISCHE ALTERNATIVE

Wilcoxon-Test für eine Stichprobe = Einstichproben-Wilcoxon-Test

Das Grundprinzip – einfach erklärt

Zunächst erkläre ich dir das Grundprinzip und zeige dir anschließend die Berechnung an einem Beispiel.

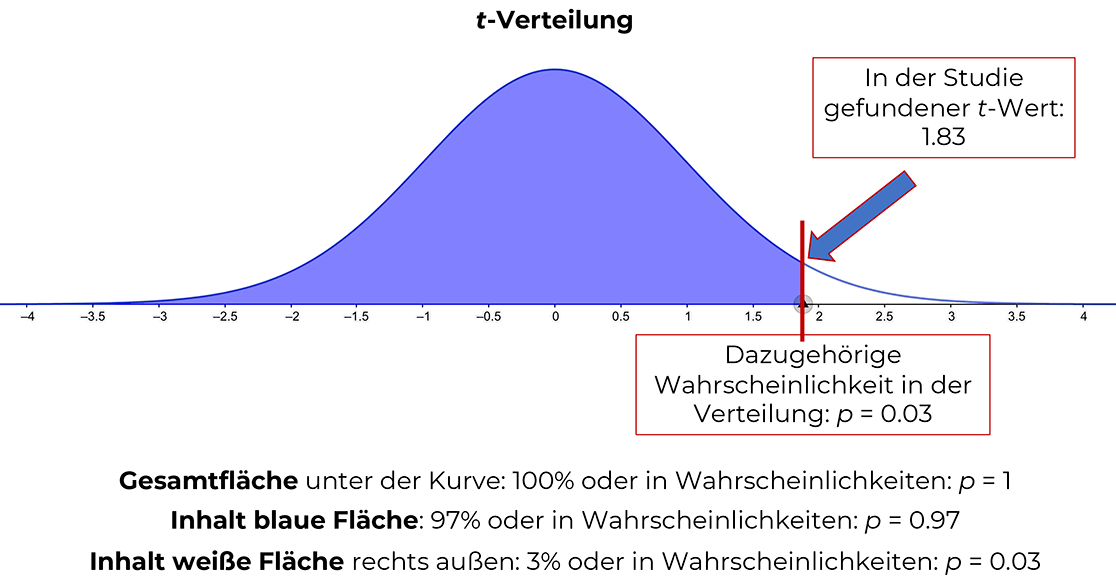
Wenn du einen t-Test durchführst, bekommst du am Ende einen sog. empirischen t-Wert heraus, der in die dazugehörige t-Verteilung hineinfällt. Diese t-Verteilung ist die Test-Verteilung für den t-Test.

Dies ist die Formel für den Einstichproben-t-Test:

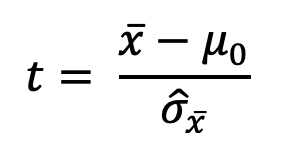
Der t-Wert (unsere "Prüfgröße") entsteht aus einem Bruch:

Im Zähler wird vom Mittelwert der Stichprobe der bereits bekannte oder angenommene Mittelwert (= Erwartungswert) abgezogen und durch den Standardfehler des Mittels im Nenner geteilt.

UND SO GEHT’S:

1. Schritt:

Du erhebst bei einer Stichprobe z. B. das Glücksgefühl nach dem Urlaub.

2. Schritt:

Daraus errechnest du den Mittelwert, die Standardabweichung (bei der Berechnung durch n – 1 teilen!) sowie den Standardfehler.

3. Schritt:

Du setzt alles in die Formel ein und erhältst den empirischen t-Wert (= der t-Wert, der aus den Daten deiner Stichprobe entsteht).

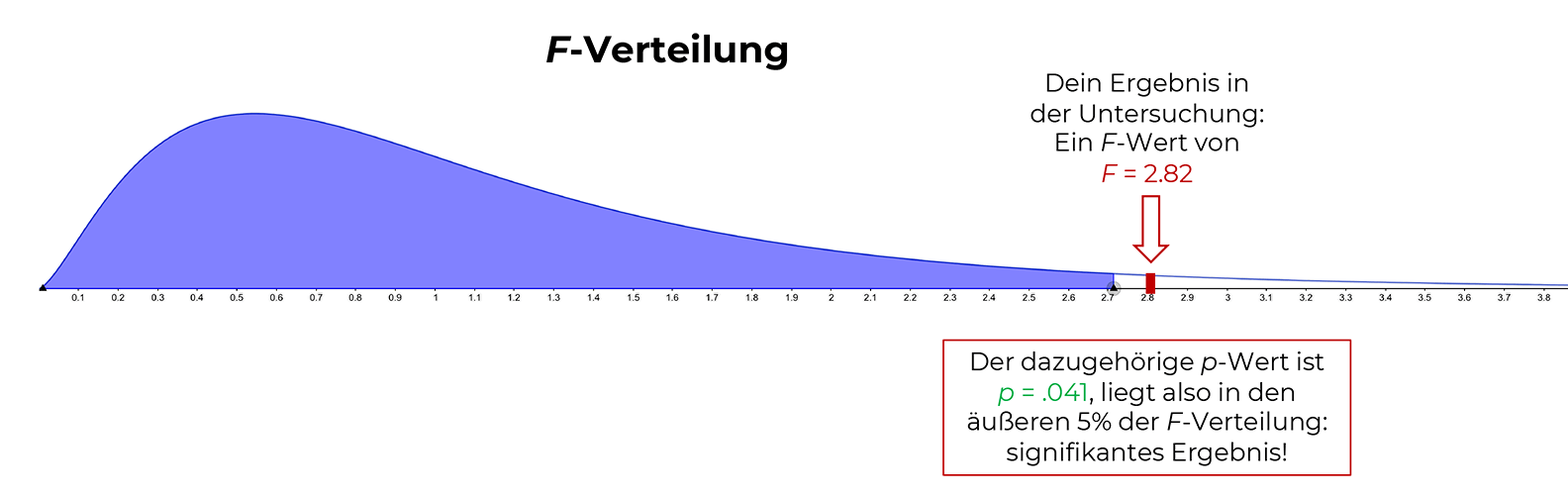
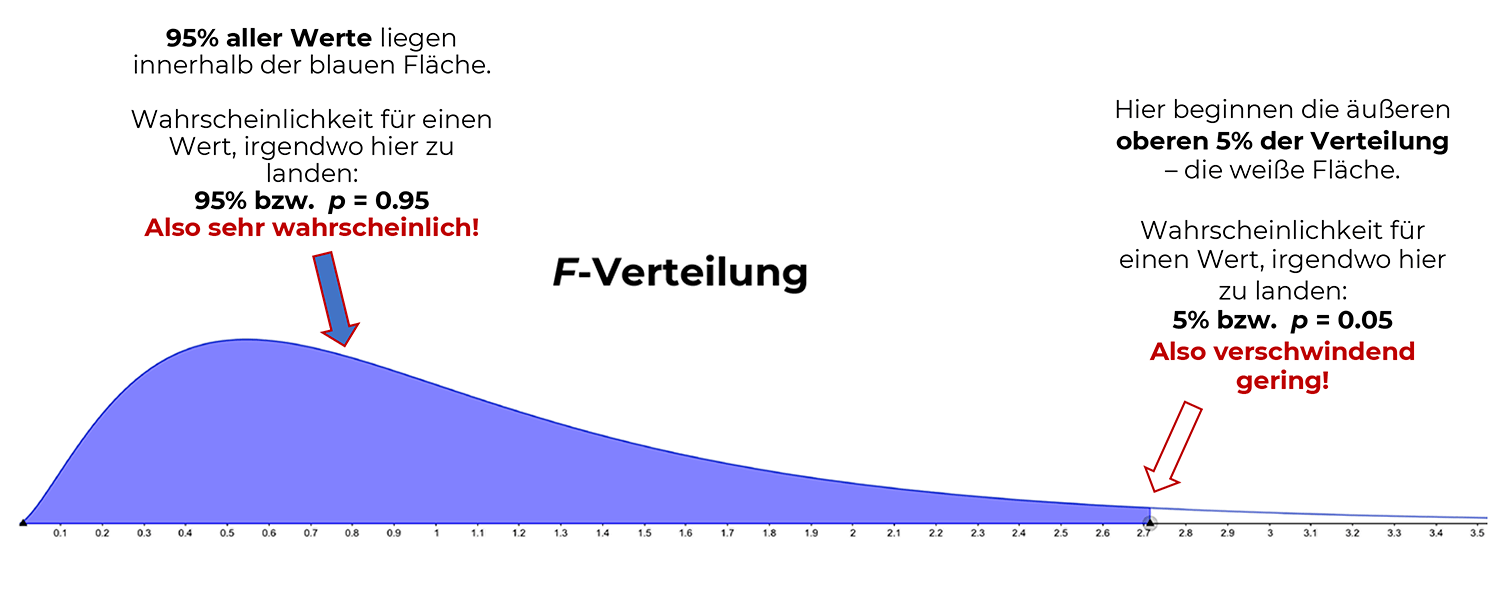
Wenn der aus den Daten der Stichprobe errechnete Mittelwert weit genug vom bekannten (oder angenommenen) Erwartungswert entfernt liegt, kommt ein empirischer t-Wert heraus, der in die äußersten Eckchen der t-Verteilung hineinfällt und somit vermutlich signifikant ist.

4. Schritt:

Um das zu überprüfen, muss der empirische t-Wert mit dem sog. kritischen t-Wert in der Tabelle der t-Verteilung verglichen werden (Näheres dazu unten).

Ist der empirische t-Wert größer (oder bei linksseitigen kleiner bzw. bei ungerichteten Hypothesen kleiner oder größer) als der kritische t-Wert, liegt ein signifikanter Unterschied vor und du verwirfst deine Nullhypothese mit deiner gewählten Irrtumswahrscheinlichkeit von z. B. 5% (Alpha = 0,05) und nimmst deine H1 an.

Wenn nicht, behältst du die Nullhypothese bei.

5. Schritt:

Wenn du ein signifikantes Ergebnis hast, berechnest du im letzten Schritt noch die dazugehörige Effektstärke Cohens d oder bei kleinen Stichproben unter N = 20 das Hedges g.

Vorgehen bei der händischen Berechnung

Überblick

Hypothesen aufstellen, Signifikanzniveau festlegen, Daten erheben, etc. = übliches Vorgehen beim Hypothesentesten
Voraussetzungen prüfen
Mittelwert, Standardabweichung und Standardfehler errechnen
Empirischen t-Wert berechnen
Freiheitsgrade bestimmen
Kritischen Wert in der t-Verteilung nachschlagen
Empirischen t-Wert mit dem kritischen t-Wert vergleichen
Bei signifikantem Ergebnis die Effektstärke Cohens d berechnen und interpretieren (= „Ist das ein praktisch bedeutsamer Effekt bzw. Unterschied?")

Welche Hypothesen aufgestellt werden können

Bevor wir zu unserem Beispiel kommen, schauen wir uns an, welche Hypothesen grundsätzlich beim Einstichproben-t-Test gebildet werden können (x steht für den Mittelwert aus den Daten der Stichprobe):

UNGERICHTETE (= ZWEISEITIGE) HYPOTHESEN

H1: x unterscheidet sich von einem bestimmten Wert

H0: Es besteht kein Unterschied zwischen x und einem bestimmten Wert

Die statistischen Hypothesen dazu:

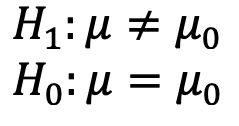
GERICHTETE (= EINSEITIGE) HYPOTHESEN

RECHTSSEITIG

H1: x ist größer als ein bestimmter Wert

H0: x ist kleiner oder gleich einem bestimmten Wert

Die statistischen Hypothesen dazu:

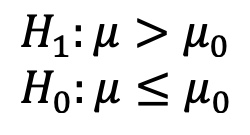
LINKSSEITIG

H1: x ist kleiner als ein bestimmter Wert

H0: x ist größer oder gleich einem bestimmten Wert

Die statistischen Hypothesen dazu:

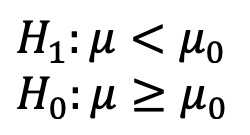
Hypothesen für unser Beispiel

H1: Das durchschnittliche Glücksgefühl nach dem Urlaub weicht signifikant von 50 ab. (= ungerichtete Hypothese)

H0: Das durchschnittliche Glücksgefühl nach dem Urlaub ist gleich 50.

STATISTISCHE HYPOTHESEN

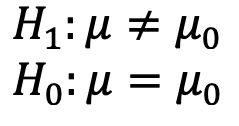
SIGNIFIKANZNIVEAU FESTLEGEN

Wir nehmen die übliche Irrtumswahrscheinlichkeit von 5%, d. h. ein Alpha von 0,05, da mit unserer Untersuchung keine größeren Konsequenzen verbunden sind.

VORAUSSETZUNGEN PRÜFEN

- Das Glücksgefühl ist intervallskaliert und daher metrisch

- Die Varianz bzw. Standardabweichung ist nicht bekannt

- Da wir 120 Personen in unserer Stichprobe haben, können wir gemäß des zentralen Grenzwertsatzes von Normalverteilung ausgehen

Wo wir hinwollen:

Formel für den Einstichproben-t-Test

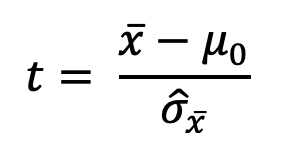
MITTELWERT & STANDARDABWEICHUNG BERECHNEN

Die Berechnung des Mittelwertes und der Standardabweichung dürfte aus der deskriptiven Statistik bekannt sein.

Bitte beachte, dass du bei der Berechnung der Standardabweichung durch n – 1 teilen musst!

STANDARDFEHLER BERECHNEN

Angenommen, bei unserer Erhebung mit n = 120 kommen ein Mittelwert von 52 sowie eine Standardabweichung von 8 heraus. Dann können wir damit den Standardfehler berechnen:

EMPIRISCHEN t-WERT BERECHNEN

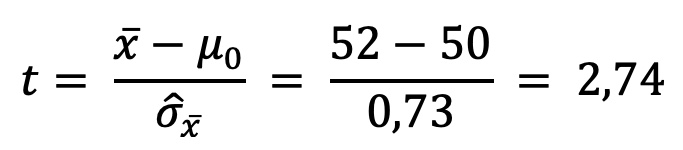
PRÜFUNG AUF SIGNIFIKANZ

Um herauszufinden, ob unser t-Wert von 2,74 signifikant ist, benötigen wir neben dem Signifikanzniveau Alpha die sog. Freiheitsgrade, auch degrees of freedom oder df genannt, sowie die Tabelle der t-Verteilung.

FREIHEITSGRADE BESTIMMEN

Für die Freiheitsgrade ziehst du von der Stichprobengröße 1 ab:

df = N – 1 = 120 – 1 = 119

KRITISCHEN t-WERT IN DER TABELLE DER t-VERTEILUNG NACHSCHLAGEN

Jetzt schnappst du dir die Tabelle der t-Verteilung und gehst auf der linken Seite bei df nach unten, bis du die 119 Freiheitsgrade findest.

Wenn du eine Tabelle verwendest, in der die exakte Anzahl an Freiheitsgraden nicht aufgeführt ist, liest du einfach beim nächstgelegenen Wert ab – das wäre hier bei 100 Freiheitsgraden. (1. Schritt)

Sobald du die richtige Zeile gefunden hast, wanderst du in der Tabelle oben so weit nach rechts, bis du dein Alpha findest.

ACHTUNG:

Wir haben hier eine ungerichtete, zweiseitige Hypothese!

Daher müssen wir unser Alpha durch 2 teilen und auf beide Seiten der Verteilung aufteilen.

Das bedeutet, dass unser empirischer t-Wert dann signifikant wird, wenn er in die unteren 2,5% oder die oberen 2,5% der t-Verteilung hineinfällt.

Daher suchen wir nun in der oberen Zeile der Tabelle den Wert 1 – Alpha : 2 = 1 – 0,025 = 0,975.

Das ist die Stelle in der t-Verteilung, an der sich von unten weg 97,5% aller Werte angesammelt haben (2. Schritt).

Im 3. Schritt suchst du dir den Schnittpunkt dieser beiden Werte und liest den kritischen t-Wert ab. Dieser zeigt an, wo die oberen 2,5% aller Werte in der t-Verteilung losgehen.

Hier sind die einzelnen Schritte:

Bei einem Alpha von 0,05 und 100 Freiheitsgraden ist der kritische Wert t = 1,984. Das bedeutet, dass ab diesem Wert die oberen 2,5% aller Werte in der t-Verteilung beginnen.

Weil die t-Verteilung symmetrisch ist, kannst du einfach nur ein Minus davor setzen und hast somit auch gleich den Wert am linken Ende der Verteilung, an dem die unteren 2,5% enden.

Du benötigst also für ein signifikantes Ergebnis entweder einen empirischen t-Wert, der größer als 1,984 oder kleiner als -1,984 ist.

Übrigens:

Es gibt verschiedene t-Tabellen, die jeweils unterschiedlich aufgebaut sind. Daher ist das nur eine grobe Beschreibung der Vorgehensweise beim Ablesen des kritischen t-Werts (= t mit einem tiefergestellten „krit"), die sich von der an deiner Hochschule verwendeten Tabelle unterscheiden kann.

WO ABLESEN BEI EINER RECHTS- ODER LINKSSEITIGEN HYPOTHESE?

RECHTSSEITIG

Hätten wir auf dem gleichen Signifikanzniveau von 5% rechtsseitig getestet, würden wir in der oberen Zeile bei 0,95 (= 1 – 0,05) bis zum Schnittpunkt mit den 100 Freiheitsgraden hinuntergehen.

Bedeutet: Du bräuchtest hier für ein signifikantes Ergebnis einen empirischen t-Wert größer 1,66.

LINKSSEITIG

Bei einer linksseitigen Hypothese würden wir zunächst wie bei der rechtsseitigen Hypothese beschrieben vorgehen und dann aufgrund der Symmetrie der Verteilung einfach ein Minus vor den gefundenen Wert von 1,66 setzen.

In diesem Fall müsste der empirische t-Wert kleiner als -1,66 sein, um signifikant zu werden.

EMPIRISCHEN t-WERT MIT DEM KRITISCHEN t-WERT VERGLEICHEN

Unser empirischer t-Wert von 2,74 ist größer als 1,984. Daher verwerfen wir die Nullhypothese und nehmen unsere Alternativhypothese mit einer 5%-igen Irrtumswahrscheinlichkeit an.

Wir können nun verkünden:

Das durchschnittliche Glücksgefühl nach dem Urlaub weicht signifikant von 50 ab.

WICHTIGER HINWEIS FÜR HINTER DIE LÖFFELCHEN:

Bei der Ergebnis-Interpretation von gerichteten Hypothesen bitte immer darauf achten, ob die Ergebnisse auch wirklich in deine postulierte Richtung gehen!

Denn du könntest ein signifikantes Ergebnis haben, das jedoch genau in die Gegenrichtung deiner Hypothese geht – und dann ist es bezogen auf deine „Ursprungs-Hypothese" NICHT signifikant.

EFFEKTSTÄRKE

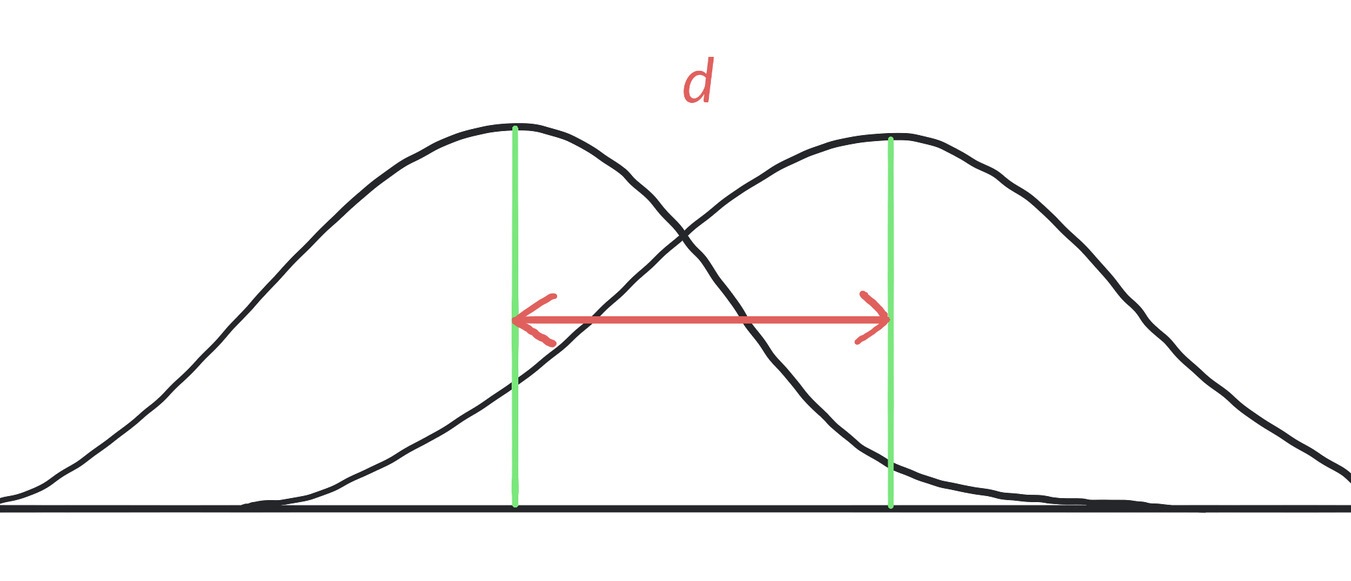
Da wir ein signifikantes Ergebnis haben, berechnen wir nun die Effektstärke Cohens d.

Cohens d sagt aus, wie groß der Unterschied zwischen den beiden Mittelwerten ist und ob es sich um einen praktisch relevanten Effekt handelt.

Hier ist die Formel dazu:

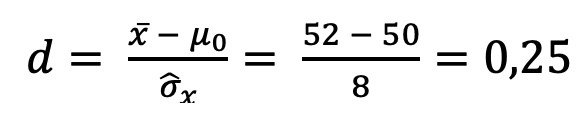
Und was bedeutet das nun?

Sofern du aus der Forschungsliteratur keinen anderen Anhaltspunkt hast, kannst du dich bei der Interpretation nach den Konventionen nach Cohen (1988) richten:

Kleiner Effekt: |0,2|

Mittlerer Effekt: |0,5|

Starker Effekt: |0,8|

Wohlgemerkt alles im Betrag!

Bedeutet: Egal, ob das Ergebnis z. B. -0,3 oder +0,3 beträgt – der Effekt ist gleich groß.

Unser Cohens d von 0,25 ist ein kleiner Effekt.

Ergebnis korrekt berichten

Du kannst das Ergebnis entweder mit Angabe von Mittelwerten (= M) und Standardabweichungen (= SD) oder ohne berichten, denn diese Angaben werden nicht immer gefordert.

Halte dich daher bitte im Zweifelsfall an das, was an deiner Hochschule Usus ist!

Hier sind beide Varianten:

Das Glücksgefühl nach dem Urlaub (M = 52, SD = 8) ist signifikant höher als 50, t(119) = 2,74, d = 0,25.

Das Glücksgefühl nach dem Urlaub ist signifikant höher als 50, t(119) = 2,74, d = 0,25.

Interpretation für Tante Erna

Wir haben untersucht, ob das Glücksgefühl nach dem Urlaub signifikant von einem „durchschnittlichen" Glücksgefühl von 50 abweicht, gemessen auf einer Skala von 0 bis 100.

Es hat sich gezeigt, dass das Glücksgefühl nach dem Urlaub signifikant höher ist als angenommen, wobei es sich um einen eher kleinen und damit praktisch wenig relevanten Unterschied handelt.

Kurz & knackig zusammengefasst

Der Einstichproben-t-Test ist das Verfahren der Wahl, wenn es um den Unterschied zwischen einem angenommenen oder bekannten Mittelwert und dem Mittelwert aus einer Stichprobe geht.

Dies erkennst du meist an Angaben wie: „Es ist bekannt, dass der Erwartungswert von x bei y liegt."

Die Varianz bzw. Standardabweichung sind unbekannt.

Es können gerichtete und ungerichtete Hypothesen getestet werden.

Falls die Voraussetzungen für den Einstichproben-t-Test verletzt sind, verwendest du als nonparametrische Alternative den Wilcoxon-Test für eine Stichprobe.

UND DAS WAR’S – GESCHAFFT! NA BITTE, GEHT DOCH!

Das war dein rundum sorglos Paket zum Einstichproben-t-Test.

Damit hast du dir jetzt redlich ein Limettentörtchen verdient!

Jetzt wünsche ich dir noch einen knackenden Tag, gutes Umsetzen und natürlich weiterhin:

HAPPY LEARNING!

QUELLEN (Als Amazon-Partnerin verdiene ich an qualifizierten Verkäufen):

Bortz, J., & Schuster, C. (2017). Statistik für Human- und Sozialwissenschaftler. Springer.

Bühner, M., & Ziegler, M. (2017). Statistik für Psychologen und Sozialwissenschaftler. Pearson.

Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed). Hillsdale, N.J: L. Erlbaum Associates.

Field, A. (2018). Discovering Statistics using IBM SPSS Statistics. SAGE.

Sedlmeier, P., & Renkewitz, F. (2018). Forschungsmethoden und Statistik für Psychologen und Sozialwissenschaftler. Pearson.

Was sind t-Tests und welche gibt es?

Hast du dich schon mal gefragt, was es mit den ganzen verschiedenen t-Tests auf sich hat?

Gefühlt gibt es ja irgendwie endlos viele Varianten – aber wie hält man die Bitteschön auseinander? Wofür sind sie überhaupt gut und wann nimmst du welchen dieser vielen t-Tests?

Die Verwirrung rund um dieses Thema wird gleich ein Ende haben, denn du erfährst, worum es grundsätzlich bei den t-Tests geht, in welchen Bereich der Statistik sie gehören, welche Arten es gibt, wie sie sich voneinander unterscheiden und noch ein paar wissenswerte Dinge mehr. Es wird also äußerst spannend…;)

Ein kleines Caveat vorab: In diesem Artikel geht es um das grundsätzliche Verständnis und nicht um die Berechnung.

Dies zeige ich dir in weiteren Blog Posts und in meinem Videokurs zur Inferenzstatistik.

Inhaltsverzeichnis

Worum geht's bei den t-Tests &

in welchen Bereich der Statistik gehören sie?

Die 3 Varianten der t-Tests

Beispiele für die 3 Varianten

Weitere t-Tests

Welche Arten von Variablen du brauchst

Die dazugehörige Testverteilung

Last, but not least:

Die dazugehörige Effektstärke

Steckbrief t-Tests

Worum geht's bei den t-Tests &

in welchen Bereich der Statistik gehören sie?

Die t-Tests gehören zu den am häufigsten verwendeten statistischen Verfahren, wenn es um Mittelwertsunterschiede bei zwei Gruppen oder Messzeitpunkten geht.

Das könnten beispielsweise Hypothesen sein wie:

Die Selbstakzeptanz ist bei Frauen niedriger als bei Männern.

Oder: Die Fokussierungsfähigkeit ist morgens höher als abends.

Die t-Tests wohnen in der Welt der schließenden oder Inferenzstatistik und hier in der Welt der Unterschiede.

Das heißt, es geht um Unterschiedshypothesen, die gerichtet, also rechts- oder linksseitig, sowie ungerichtet sein können.

Die 3 Varianten der t-Tests

t-Tests gliedern sich in 3 VARIANTEN:

Einstichproben-t-Test
t-Test für unabhängige Stichproben, auch ungepaarter t-Test genannt
t-Test für abhängige Stichproben, auch gepaarter t-Test oder t-Test bei verbundenen Stichproben genannt

Da es bei allen Varianten um Mittelwerts-Unterschiede bei 2 Gruppen oder zwei Messzeitpunkten geht, bedeutet das:

die Zahl 2 ist hier zentral!

Daher hinter die feinen Löffelchen schreiben:

Wenn Mittelwertsunterschiede bei ZWEI Gruppen oder Messzeitpunkten

das Thema deiner Hypothese sind,

wählst du gewöhnlich einen der t-Tests

– natürlich nur, sofern die Voraussetzungen dafür erfüllt sind.

Hast du 3 oder mehr Gruppen bzw. Messzeitpunkte,

kannst du keine t-Tests mehr rechnen,

sondern musst in die Welt der Varianzanalyse (= ANOVA) wechseln!

Beispiele für die 3 Varianten

Einstichproben-t-Test

Wie der Name bereits erahnen lässt, geht’s hier um den Mittelwert EINER Stichprobe, der mit einem bekannten (oder vermuteten) Mittelwert verglichen wird. Es bleibt also trotz des Namens beim Vergleich zweier Mittelwerte.

Mit Vergleich ist gemeint, dass es um die Differenz der beiden Mittelwerte geht, die dann je nach Verfahren noch weiter modifiziert wird.

Letztlich geht’s um die Frage: Unterscheiden sich die Mittelwerte signifikant in der erwarteten Richtung, liegen sie also weit genug auseinander? Dies trifft auf rechts- oder linksseitige Hypothesen zu.

Und bei ungerichteten Hypothesen ist die Frage: Unterscheiden sie sich signifikant, d. h. liegen sie weit genug auseinander, egal in welcher Richtung?

Wie könnte eine Fragestellung beim Einstichproben-t-Test lauten?

Angenommen, du vermutest, dass die durchschnittliche Intelligenz der Bayern höher ist als der typische Deutschland-weite durchschnittliche IQ von 100 IQ-Punkten.

Das wäre eine rechtsseitige Unterschiedshypothese, bei der du dir beispielsweise 50 testwillige Bayern und Bayerinnen suchen und sie einem IQ-Test unterziehen würdest.

Aus den 50 IQ-Werten berechnest du dann das arithmetische Mittel und schaust, ob es signifikant höher ist als der durchschnittliche IQ von 100.

Selbstverständlich ist die Berechnung und Vorgehensweise deutlich komplexer, aber das ist das Grundprinzip.

Wie das genau bei allen 3 t-Test-Arten geht, erkläre ich dir gerne in meinem Powerkurs “Inferenzstatistik & SPSS leicht gemacht!” – der rundum sorglos Videokurs, der dich fit für die Prüfung macht!

Guckst du hier:

t-Test für unabhängige Stichproben

Hier werden die Mittelwerte zweier unabhängiger Gruppen miteinander verglichen.

Das könnte eine Hypothese sein wie:

Die Frustrationstoleranz ist bei jüngeren Menschen niedriger als bei älteren. (Linksseitige Hypothese)

Damit hast du zwei Gruppen, die voneinander unabhängig sind: Jüngere und ältere Menschen, bei denen jeweils die Frustrationstoleranz erhoben wird.

Dann werden aus den Werten jeder Gruppe wiederum die Mittelwerte berechnet und diese miteinander verglichen – wohlgemerkt muss man wie bereits erwähnt noch mehr tun, aber das nur fürs grobe Verständnis.

Unabhängige Stichproben bedeutet übrigens, dass die Menschen in den beiden Gruppen nichts miteinander zu tun haben, also in keiner Weise irgendwie miteinander "verbandelt" sind.

t-Test für abhängige Stichproben

Man ahnt es: Es könnte ebenfalls um den Vergleich zweier Mittelwerte gehen, doch nun bei abhängigen Stichproben.

Jetzt wird’s von den Anwendungsmöglichkeiten her etwas komplizierter, weil es – und das gilt ganz generell für statistische Verfahren – drei verschiedene Arten von abhängigen Stichproben gibt, nämlich die folgenden:

Mehrmalige Messungen bei denselben Personen zu verschiedenen Messzeitpunkten
Messungen bei in irgendeiner Weise miteinander verbundenen Personen wie z. B. Ehepaare, Lebensgefährtinnen, Geschwister, Team-Kolleginnen, etc. sowie:
Mehrmalige Messungen bei denselben Personen unter verschiedenen Bedingungen bzw. „Treatments“

Schauen wir uns zuerst den 1. Fall: “Mehrmalige Messungen bei denselben Personen zu verschiedenen Messzeitpunkten” an.

Die Hypothese lautet: Die soziale Kompetenz Jugendlicher ist nach einem Kompetenz-Training höher als zuvor.

Das wäre eine rechtsseitige Hypothese.

Hier wird die soziale Kompetenz bei Jugendlichen vor und nach Absolvieren eines Trainings zur Steigerung der sozialen Kompetenz erhoben und die beiden Mittelwerte miteinander verglichen.

2. Fall: Messungen bei miteinander verbundenen Personen

Die Hypothese ist: Zwillinge unterscheiden sich in ihrer Extraversion, eine ungerichtete Hypothese

3. Fall: Mehrmalige Messungen bei denselben Personen unter verschiedenen Bedingungen bzw. Treatments

Unsere Hypothese lautet: Die Lebenszufriedenheit ist nach dem Verzehr von Sachertorte geringer als nach dem Verzehr von Schwarzwälder Kirschtorte, eine linksseitige Hypothese.

Jede Person bekommt zwei Torten vorgesetzt und nach dem Verzehr jeder Torte wird die Lebenszufriedenheit gemessen.

Hier geht es also nicht um den Vergleich von Messzeitpunkten, sondern um die Reaktionen auf verschiedene Treatments.

Natürlich werden die Torten streng genommen auch nicht gleichzeitig konsumiert, aber das Interessierende sind nicht die Werte zu unterschiedlichen Zeitpunkten, sondern die Ergebnisse oder Reaktionen nach dem Verzehr verschiedener Dinge.

Weitere t-Tests

Gut zu wissen:

Damit’s nicht allzu langweilig wird, gibt’s darüber hinaus auch noch andere t-Tests, die zur Signifikanz-Prüfung von beispielsweise Korrelationen wie dem Korrelationskoeffizienten r nach Bravais-Pearson oder den Regressionskoeffizienten b eingesetzt werden.

Bei diesen geht es aber inhaltlich nicht um Mittelwerts-Unterschiede!

Zurück zu den 3 klassischen t-Tests:

Welche Arten von Variablen du brauchst

Bei allen t-Tests ist die Gruppen-Variable (= wer unterscheidet sich von wem?) kategorial, d. h. nominal- oder ordinalskaliert.

Du kannst auch höher skalierte Variablen verwenden, musst sie dann jedoch „downgraden“, d. h. in Kategorien verpacken:

Das Einkommen (Verhältnisskala) könnte beispielsweise in hoch / niedrig umgewandelt werden.

Die Gruppen-Variable bzw. die Messzeitpunkte sind die UV.

Die AV (= das, was gemessen wird) ist metrisch und normalverteilt, mit unbekannter Standardabweichung in der Grundgesamtheit.

Da es immer nur um den Vergleich von zwei Gruppen geht, kannst du dennoch Gruppen-Variablen mit mehr als 2 Ausprägungen verwenden, sofern du daraus nur die zwei interessierenden Ausprägungen in deine Hypothese aufnimmst.

Ein Beispiel hierzu:

Angenommen, du erhebst als AV das Glücksgefühl nach dem Urlaub und als UV die Urlaubsart in den 4 Ausprägungen:

Busreise nach Kärnten mit dem Kegelclub
Käfigtauchen mit weißen Haien in Australien
Lachyoga-Retreat auf Bali
Faultier-Spotting in Costa Rica

Wenn dich aber ausschließlich der Unterschied im Glücksgefühl nach dem Urlaub zwischen den Busreisenden mit dem Kegelclub und den Lach-Yogis interessiert, verwendest du für die Berechnung nur die Daten der Busreisenden und der Yogis.

Deine Hypothese würde dann lauten: Busreisende und Lach-Yogis unterscheiden sich in ihrem Glücksgefühl nach dem Urlaub.

D. h., du verwendest für den t-Test also nur diese zwei Ausprägungen deiner vierfach gestuften UV Urlaubsart und ignorierst die Daten der anderen Urlaubsgruppen.

Das Gleiche gilt für mehrere Messzeitpunkte wie z. B. morgens, mittags, abends und nachts, von denen dich nur zwei interessieren:

Dann verwendest du für deine Hypothese beispielsweise nur die Messungen morgens und abends und vergleichst diese miteinander.

Die dazugehörige Testverteilung

Eine Testverteilung ist eine theoretische Verteilung von Werten, in die das Ergebnis deiner Berechnungen hineinfällt.

Die zu den t-Tests dazugehörige Testverteilung ist die t-Verteilung.

Wenn wir uns bei unserem t-Test den Wolf gerechnet haben, erhalten wir am Ende einen schicken t-Wert, der in die dazugehörige t-Verteilung hineinfällt.

Und dann gilt wie immer beim Hypothesentesten:

Fällt er in das äußerste, durch das Signifikanzniveau alpha definierte Eckchen der Verteilung?

Wenn ja, besteht ein signifikanter Unterschied, und wenn nicht, dann nicht ;).

Dazu noch etwas Wesentliches für hinter die Löffelchen:

Wichtig ist immer, bei der Ergebnis-Interpretation von rechts- oder linksseitigen Hypothesen darauf zu achten, ob die Ergebnisse auch wirklich in die erwartete Richtung gehen!

Denn es könnte ja sein, dass der resultierende t-Wert vermeintlich signifikant ist, weil er in das äußerste Eckchen der t-Verteilung hineinfällt.

Wenn er aber in die Gegenrichtung der Hypothese, also in die andere Seite hineinfällt, haben wir tatsächlich gar kein signifikantes Ergebnis!

Daher bitte bei gerichteten Hypothesen immer darauf achten,

ob das Ergebnis auch wirklich in die erwartete Richtung geht!

Last, but not least:

Die dazugehörige Effektstärke

Du weißt vermutlich, dass man bei einem signifikanten Ergebnis stets eine passende Effektstärke berechnen sollte, um herauszufinden, ob der gefundene Unterschied auch praktisch bedeutsam ist.

Zum Leidwesen der Studierenden existieren verschiedene Effektstärken für die t-Tests, wobei Cohens d die gängigste ist, die bei allen 3 t-Tests zum Einsatz kommen kann.

Cohens d sagt aus, wie groß der Unterschied zwischen den beiden Mittelwerten ist. Und wenn dich der unstillbare statistische Wissensdurst plagt, kannst du dir dazu meinen Blog Post zu Cohens d durchlesen – da findest du Genaueres hierzu.

Darüber hinaus lassen sich je nach Art des t-Tests auch Hedges g, Glass Delta oder der Korrelationskoeffizient r nach Bravais-Pearson berechnen.

Zum Abschluss noch ein kleiner Steckbrief:

Steckbrief t-Tests

Du verwendest einen der t-Tests, wenn es um Mittelwerts-Unterschiede bei zwei Gruppen oder Messzeitpunkten geht
Den t-Test gibt es in 3 verschiedenen Varianten: Einstichproben-t-Test, t-Test für unabhängige und t-Test für abhängige Stichproben
Sie gehören in die schließende Statistik und hier in die Welt der Unterschiedshypothesen
Die AV ist metrisch und normalverteilt mit unbekannter Varianz / Standardabweichung
Die UV ist kategorial (= nominal- oder ordinalskaliert)
Es können gerichtete und ungerichtete Hypothesen getestet werden
Bei gerichteten Hypothesen ist darauf zu achten, ob die Ergebnisse auch wirklich in die erwartete Richtung gehen
Die dazugehörige Test-Verteilung ist die t-Verteilung
Die dazugehörige Effektstärke ist gewöhnlich das Cohens d

UND DAS WAR’S – GESCHAFFT! NA BITTE, GEHT DOCH!

Das war deine Einführung in die bunte und vor allem aufregende Welt der t-Tests.

Jetzt wünsche ich dir noch einen knackenden Tag und natürlich weiterhin:

HAPPY LEARNING!

QUELLEN (Als Amazon-Partnerin verdiene ich an qualifizierten Verkäufen):

Bühner, M., & Ziegler, M. (2017). Statistik für Psychologen und Sozialwissenschaftler. München: Pearson.

Sedlmeier, P., & Renkewitz, F. (2018). Forschungsmethoden und Statistik für Psychologen und Sozialwissenschaftler. München: Pearson.

Bortz, J., & Schuster, C. (2017). Statistik für Human- und Sozialwissenschaftler. Berlin: Springer.

Field, A. (2018). Discovering Statistics using IBM SPSS Statistics. London: SAGE.

KENNST DU SCHON MEINEN YOUTUBE-KANAL?

Guckst du hier:

ICH WILL ZUM YOUTUBE-KANAL!

Wann verwende ich welche Methode?

Die Frage aller Fragen im Statistik-geplagten Leben der meisten Studierenden: t-Test oder Varianzanalyse? Oder lieber doch Regression? Nein? Chi-Quadrat vielleicht?

Doch nun ist Schluss mit dem heiteren Methoden-Raten, denn es naht Abhilfe. Guckst du...

Methodenwahl Variante 1: Entscheidungsbäume

Im Internet oder Lehrbüchern findest du ein Füllhorn an mehr oder weniger komplexen Entscheidungsbäumen, die dir helfen, die richtige Methode auszuwählen.

Sie führen dich mit gezielten Fragen wie z. B. "Wie viele abhängige Variablen (AVn)? Eine oder mehrere?", "Welches Skalenniveau hat die unabhängige Variable (UV)?" zum Methodenglück.

Hier ist eine kleine, aber feine Auswahl an frei im Internet verfügbaren Entscheidungsbäumen:

Methodenwahl Variante 2: Worum geht's inhaltlich?

Die allermeisten Hypothesen in der Statistik in den Sozialwissenschaften drehen sich um:

Unterschiede
Zusammenhänge
Veränderungen über die Zeit hinweg

Daher kannst du das als Anhalts- bzw. Startpunkt dafür nehmen, welche Methode du verwenden solltest.

Frag' dich also immer zu Beginn: worum geht es inhaltlich bei meiner Hypothese?

Wenn du den Grob-Bereich weißt (Unterschiede, Zusammenhänge oder Veränderungen), kannst du dich dann im jeweiligen Bereich mit den nachfolgenden Fragen weiter vorantasten:

Wenn es um Unterschiede geht...

Beispiele:

Frauen sind weniger konfliktbereit als Männer (t-Test für unabhängige Stichproben).

Drei verschiedene Trainings zur sozialen Kompetenz unterscheiden sich in ihrer Wirksamkeit (Varianzanalyse für unabhängige Messungen).

Zwillinge unterscheiden sich in ihrer Risikoaversion (t-Test für abhängige Stichproben).

Die dazugehörigen Fragen...

Wie viele Gruppen werden miteinander verglichen?

2 Gruppen & NORMALVERTEILTE AV:

Unabhängige oder abhängige Stichproben?

- Unabhängige Stichproben: t-Test für unabhängige Stichproben

- Abhängige Stichproben: t-Test für abhängige Stichproben

2 GRUPPEN & NICHT NORMALVERTEILTE BZW. ORDINALSKALIERTE AV:

UNABHÄNGIGE ODER ABHÄNGIGE STICHPROBEN?

- Unabhängige Stichproben: Mann-Whitney-U-Test

- Abhängige Stichproben: Wilcoxon-Test

Mindestens 3 Gruppen & NORMALVERTEILTE AV:

Unabhängige oder abhängige Stichproben?

- Unabhängige Stichproben: "normale" Varianzanalyse für unabhängige Messungen

- Abhängige Stichproben: Varianzanalyse mit Messwiederholung

Mindestens 3 GRUPPEN & NICHT NORMALVERTEILTE bzw. Ordinalskalierte AV:

UNABHÄNGIGE ODER ABHÄNGIGE STICHPROBEN?

- Unabhängige Stichproben: Kruskal-Wallis-Test / Rangvarianzanalyse

- Abhängige Stichproben: Friedman-Test

Wenn es um Zusammenhänge geht...

Beispiele:

Es besteht ein Zusammenhang zwischen der kognitiven Verarbeitungstiefe und dem Alter (Korrelationskoeffizient r nach Bravais-Pearson).

Das gewählte Studienfach ist abhängig vom Geschlecht (Chi-Quadrat-Test auf Unabhängigkeit).

Je höher der Bildungsgrad, desto höher die Einschätzung des Selbstvertrauens als gering, mittelstark und stark ausgeprägt (Kendalls Tau b).

Die dazugehörigen Fragen...

WELCHES SKALENNIVEAU HABEN Deine VARIABLEN?

2 NOMINALSKALIERTE VARIABLEN:

- Nicht normiertes Maß: Chi-Quadrat-Koeffizient & Chi-Quadrat-Test auf Unabhängigkeit

- Dichotome Variablen: Phi-Koeffizient

- Normiertes Maß: Cramers V

- Normiertes Maß: Kontingenz-Koeffizient C

2 ORDINALSKALIERTE VARIABLEN:

- Zwei originär ordinalskalierte Merkmale: Kendalls Tau b

- Zwei metrische Merkmale, die jedoch die Voraussetzungen für den Korrelationskoeffizienten r nach Bravais-Pearson nicht erfüllen (nicht normalverteilt oder keine Linearität): Rangkorrelationskoeffizient nach Spearman

2 metrische VARIABLEN:

- Linearer Zusammenhang, nicht normiertes Maß: Kovarianz

- Linearer Zusammenhang, normiertes Maß: Korrelationskoeffizient r nach Bravais-Pearson

Unterschiedlich skalierte VARIABLEn:

- 1 dichotom, 1 intervallskaliert: Punktbiseriale Korrelation

- 1 dichotom, 1 ordinalskaliert: Biseriale Korrelation

Wenn es um Veränderungen über die Zeit hinweg geht...

Beispiele:

Die Aufmerksamkeitsspanne ist morgens höher als abends (t-Test für abhängige Stichproben).

Nach einem Seminar über das Rauchen gibt es weniger Raucher und mehr Nicht-Raucher (McNemar-Test).

Die Lernmotivation verändert sich im Verlauf des Studiums: gemessen vor dem Studium, nach dem 1., 3. und 6. Semester (Varianzanalyse mit Messwiederholung).

Die dazugehörigen Fragen...

Wie viele Messzeitpunkte?

2 MESSZEITPUNKTE:

Skalenniveau der AV?

- Metrische normalverteilte AV: t-Test für abhängige Stichproben

- Metrische NICHT normalverteilte AV oder ordinalskalierte AV: Wilcoxon-Test

- Dichotome nominalskalierte Variable: McNemar-Test

Mindestens 3 MESSZEITPUNKTE:

- Metrische AV: Varianzanalyse mit Messwiederholung

- Metrische NICHT normalverteilte AV oder ordinalskalierte AV: Friedman-Test

Meine Challenge an Dich:

Schnapp' dir doch gleich mal eine Fragestellung, mit der du dich gerade beschäftigst, und probier' aus, was dir mehr liegt, um zur richtigen Methode zu kommen:

Entscheidungsbäume oder die Herangehensweise nach inhaltlichen Gesichtspunkten?

Viel Erfolg!

KENNST DU SCHON MEINEN YOUTUBE-KANAL?

Guckst du hier:

ICH WILL ZUM YOUTUBE-KANAL!

Quellen:

Bortz, J., & Schuster, C. (2017). Statistik für Human- und Sozialwissenschaftler. Berlin: Springer.

Field, A. (2018). Discovering Statistics using IBM SPSS Statistics. London: SAGE.

Sedlmeier, P., & Renkewitz, F. (2018). Forschungsmethoden und Statistik für Psychologen und Sozialwissenschaftler. München: Pearson.

Standardfehler des Mittels einfach erklärt!

In der Statistik hat man's ja zur allgemeinen Verwirrung ganz gern mit dem Wort "Standard" in allen erdenklichen Variationen: Standardabweichung, Standardnormalverteilung, Standardisierung, Standardschätzfehler – und last, but not least: Standardfehler! Letzteren werde ich dir hier nahebringen. Kurz & knackig: der Standardfehler des Mittels ist die Standardabweichung in einer THEORETISCHEN Verteilung von unendlich vielen Mittelwerten.

Inhaltsverzeichnis

Was ist der Standardfehler?

In welchen Bereich der Statistik gehört er?

Wie wird der Standardfehler berechnet?

Wie wird der Standardfehler interpretiert?

Steckbrief Standardfehler des Mittels

Meine Challenge an dich

Was ist der Standardfehler?

Stell' dir vor, du machst eine Studie zur Resilienz bei Erwachsenen in Deutschland. Dazu fängst du 150 Erwachsene über 18 Jahren ein und zwingst sie zu einem Resilienztest.

Nun hast du 150 Resilienz-Werte, erhoben auf einer Skala von 0 (= gar nicht vorhanden) bis 100 (= der Fels / die Felsin in der Brandung). Aus diesen berechnest du (oder vermutlich eher SPSS) den Mittelwert.

Jetzt pinselst du liebevoll eine Skala und trägst den gefundenen Mittelwert auf der x-Achse ein.

Weil du so inspiriert und im Flow warst, machst du das Ganze gleich nochmal, an derselben Grundgesamtheit zur selben Fragestellung mit demselben Messinstrument für Resilienz.

Und nochmal. Und nochmal. Und nochmal. Das sieht dann irgendwann so aus:

Vermutlich würdest du dir spätestens beim dritten Mal den Unmut der Befragten einhandeln, aber das hält dich nicht auf.

Du machst weiter... ad infinitum und pinselst immer wieder die gefundenen Mittelwerte auf der x-Achse auf.

Dort, wo besonders viele Mittelwerte hinfallen, bildet sich ein "Huckel" und irgendwann entsteht aus all diesen Mittelwerten eine wunderschöne und sehr ansehnliche Normalverteilungskurve.

Wie du vermutlich schon gelernt hast, hat diese Normalverteilung ebenfalls wieder einen Mittelwert, also der Wert, der genau in der Mitte der Kurve, am höchsten Punkt, liegt.

Dieser Mittelwert aller Mittelwerte ist der Erwartungswert "mü", also der tatsächlich in der Population geltende Mittelwert, hier in grün eingezeichnet:

Und zu beiden Seiten um diesen Mittelwert herum gibt es auch eine Standardabweichung: das ist der Standardfehler. Der Standardfehler ist daher die Standardabweichung in einer theoretischen Verteilung von Mittelwerten.

Denn wie du dir denken kannst, macht das natürlich kein ! Das ist also eine rein theoretische Vorstellung. In der Praxis nimmt man nur eine repräsentative und zufällig ausgewählte Stichprobe und berechnet daraus den Standardfehler.

Und was sagt uns der Standardfehler bzw. wofür brauchen wir ihn?

Der Standardfehler des Mittels ist ein Maß dafür, wie gut der Mittelwert einer Stichprobe den Populationsmittelwert mü schätzt.

Je kleiner, desto besser trifft unser x quer den tatsächlich in der Grundgesamtheit geltenden Erwartungswert mü.

Hier siehst du den Standardfehler zu beiden Seiten des Mittelwerts / Erwartungswerts in gelb eingezeichnet:

In welchen Bereich der Statistik gehört er?

Der Standardfehler gehört in die Welt der Inferenzstatistik und dort in den Bereich des theoretischen Grundwissens.

Dieses Wissen legt den Grundstein für das Verständnis der verschiedenen Verteilungen und darauf aufbauenden Methoden. Er ist nur bei metrischen Variablen anwendbar, d. h. ab Intervallskala.

Wie wird der Standardfehler berechnet?

Dies ist die Formel:

An der Formel kannst du sehen, dass der Standardfehler als Sigma (= Standardabweichung in der Population / Grundgesamtheit) mit einem tiefergestellten x quer definiert ist: als Standardabweichung in einer Verteilung von ganz vielen bunten Mittelwerten.

2 Schritte führen zum Standardfehler-Glück:

1. Standardabweichung aus deinen Stichproben-Daten berechnen

2. Durch Wurzel aus n teilen

Kommen wir zu unserem Resilienz-Beispiel zurück. Da ich dich hier nicht mit 150 Werten belasten will, beschränken wir uns auf eine Stichprobe von sagenhaften 8 Personen.

Resilienz-Werte: 56 80 66 74 59 65 48 70

Standardabweichung: 10.26 (wenn man durch n – 1 teilt!)

Mittelwert: 64.75

Beispiel größerer Datensatz:

Angenommen, wir würden die Untersuchung tatsächlich mit 150 Personen machen und würden auch dort eine Standardabweichung von 10.26 herausbekommen.

Dann sähe der Standardfehler des Mittels folgendermaßen aus:

Du siehst also, dass er deutlich kleiner geworden ist. Daher gilt:

Je größer die Stichprobe, desto kleiner der Standardfehler und desto genauer die Schätzung des Populationsmittelwerts!

Wie wird der Standardfehler interpretiert?

Hier gibt es leider keine klaren Regeln oder Konventionen!

Wichtig ist wie bei den meisten anderen statistischen Interpretationen auch, dass du die verwendete Skala im Hinterkopf behältst. Denn je nachdem wie groß die Skala ist, wirst du zu einer unterschiedlichen Interpretation kommen.

Idealerweise liegt der Standardfehler des Mittels jedoch unter 1.

Wie sag' ich's Tante Erna?

Stell' dir vor, du bist bei deiner Tante Erna zu Schwarzwälder Kirschtorte und ordentlich Kaffee eingeladen. Tante Erna ist nicht die allerfirmste in Statistik, aber stets super interessiert an allem, was du so erhebst.

Also musst du ihr deine Ergebnisse in lai*innen-verständlicher Form nahebringen.

Das sähe hier so aus:

"Die Versuchspersonen waren insgesamt überdurchschnittlich psychisch widerstandsfähig." = Mittelwert von 64.75 auf einer Skala von 0 – 100

"Man kann davon ausgehen, dass das Ergebnis ziemlich gut das Gros aller Erwachsenen in Deutschland widerspiegelt." = Standardfehler von 0.84

Zum Abschluss noch ein Steckbrief:

Steckbrief Standardfehler des Mittels

= Standardabweichung einer theoretischen Verteilung von unendlich vielen Mittelwerten
Maß dafür, wie gut der Mittelwert einer Stichprobe den Populationsmittelwert mü schätzt
Nur bei metrischen Variablen anwendbar
Je größer die Stichprobe, desto kleiner der Standardfehler und desto genauer die Schätzung des Populationsmittelwerts
Bei der Interpretation immer die verwendete Skala und die Größe des Mittelwerts im Auge behalten!

Meine Challenge an dich

Schnapp' dir doch gleich mal einen Datensatz, den du entweder bereits hast oder erfinde einen.

Und dann rechne bitte den Standardfehler aus und versuch' dich an einer Interpretation für Tante Erna.

Viel Spaß!

KENNST DU SCHON MEINEN YOUTUBE-KANAL?

Guckst du hier:

ICH WILL ZUM YOUTUBE-KANAL!

Fühlst du dich lost im dschungel der Statistischen methoden?

Dann schnapp' dir das E-Book (0,-€):

endlich durchblick in statistik!

in 4 einfachen schritten zur wahl der richtigen methode

ich will das E-Book!

Quellen:

Bortz, J., & Schuster, C. (2017). Statistik für Human- und Sozialwissenschaftler. Berlin: Springer.

Field, A. (2018). Discovering Statistics using IBM SPSS Statistics. London: SAGE.

Sedlmeier, P., & Renkewitz, F. (2018). Forschungsmethoden und Statistik für Psychologen und Sozialwissenschaftler. München: Pearson.

Wahrscheinlichkeitsfunktion einfach erklärt!

Wenn du eine Untersuchung mit diskreten Variablen machst, also Variablen, die nominal- oder ordinalskaliert sind, und du gerne auf einen Blick sehen möchtest, wie wahrscheinlich welche Ausprägungen sind, brauchst du dafür die Wahrscheinlichkeitsfunktion.

Inhaltsverzeichnis

Was ist eine Wahrscheinlichkeitsfunktion?

In welchen Bereich der Statistik gehört sie?

Wie entsteht die Wahrscheinlichkeitsfunktion?

Steckbrief Wahrscheinlichkeitsfunktion

Was ist eine Wahrscheinlichkeitsfunktion?

Grundsätzlich stellt eine "Funktion" eine Beziehung zwischen zwei Mengen dar. Sie ordnet den Ausprägungen der einen Menge jeweils eine bestimmte Ausprägung der anderen Menge zu, zum Beispiel jedem Wert auf der x-Achse einen bestimmten Wert auf der y-Achse.

Eine Wahrscheinlichkeitsfunktion (oder auch Zähldichte) ordnet jeder möglichen Ausprägung einer diskreten Variablen (x-Achse) in einer hübschen Grafik eine bestimmte Wahrscheinlichkeit auf der y-Achse zu.

Sie ist also eine visuelle Darstellung der Auftretenswahrscheinlichkeiten von bestimmten Ausprägungen einer Variablen. Diese Auftretenswahrscheinlichkeiten entsprechen konzeptuell den relativen Häufigkeiten.

Dabei ist der Unterschied zur Dichtefunktion, dass es sich hier um diskrete Variablen oder Merkmale handelt. Hier gibt es zwischen zwei Ausprägungen nichts, da ist quasi ein "Loch" – im Gegensatz zu den stetigen Variablen, wo zwischen zwei Ausprägungen unendlich viele Werte liegen können.

Studienfächer sind beispielsweise diskrete Variablen: da gibt es nichts zwischen Ägyptologie und Alt-Islamistik oder BWL. Daher erfolgt die Darstellung auch nicht in einer Fläche wie bei der Dichtefunktion, sondern mit Säulen, Stäbchen oder Balken für die Wahrscheinlichkeiten der EINZELNEN Ausprägungen.

Wenn du jedoch z. B. bei einem Würfelexperiment berechnen möchtest, wie wahrscheinlich das Werfen von höchstens dreimal 6 oder mindestens zweimal die 1 ist, dann brauchst du die Verteilungsfunktion, die quasi einer "Aufeinanderstapelung" der Einzelwahrscheinlichkeiten entspricht.

In welchen Bereich der Statistik gehört sie?

Die Wahrscheinlichkeitsfunktion gehört in die Welt der Inferenzstatistik und dort in den Bereich des theoretischen Grundwissens.

Dieses Wissen brauchst du, um zu verstehen, wie die verschiedenen Verteilungen zustandekommen, was man mit ihnen machen kann und wie man Wahrscheinlichkeiten berechnet. Diskrete Verteilungen sind z. B. die Binomial- oder Hypergeometrische Verteilung (wir erinnern uns mit Freuden an die schönen Glücksrad- oder Lotto-Aufgaben....;).

Wie entsteht die Wahrscheinlichkeitsfunktion?

Angenommen, du untersuchst 120 zufällig ausgewählte Personen und erhebst deren Geschlecht in den Ausprägungen Frau, Mann und Divers. 56 Personen geben ihr Geschlecht als weiblich an, 60 als männlich und 4 als divers.

Nun berechnest du die relativen Häufigkeiten, indem du die jeweilige Ausprägungsanzahl durch die Gesamt-Stichprobengröße N teilst:

Frau: 56 : 120 = 0.47

Mann: 60 : 120 = 0.5

Divers: 4 : 120 = 0.03

Diese relativen Häufigkeiten entsprechen jetzt den Wahrscheinlichkeiten: die Wahrscheinlichkeit, beispielsweise eine Frau zu ziehen, liegt bei 0.47 oder bei 47%.

Dies wird nun folgendermaßen aufgepinselt:

Auf der x-Achse trägst du die vorkommenden Ausprägungen ein: Frau, Mann und Divers.

Dann markierst du liebevoll die y-Achse mit Wahrscheinlichkeiten (immer zwischen 0 und 1) und ziehst die zu den jeweiligen Ausprägungen dazugehörigen Balken bis zum vorher von dir errechneten Punkt. Hier: 0.47 für die Frauen, 0.5 für die Männer und 0.03 für Divers. Das sieht dann folgendermaßen aus (liebevoll von mir gemalt):

Und das war's auch schon!

Übrigens: f(x), was du oben an der y-Achse siehst, bedeutet "Funktion von x", also in diesem Falle die Zuordnung der Einzelwahrscheinlichkeiten zu den jeweiligen Geschlechts-Ausprägungen.

Zum Abschluss noch ein superkurzer Steckbrief:

Steckbrief Wahrscheinlichkeitsfunktion

Wird auch Zähldichte genannt
Nur für diskrete Variablen möglich!
Visuelle Darstellung von Auftretenswahrscheinlichkeiten einzelner Merkmalsausprägungen
Die Auftretenswahrscheinlichkeiten entsprechen konzeptuell den relativen Häufigkeiten
Gehört zum Basiswissen für die schließende oder Inferenzstatistik

KENNST DU SCHON MEINEN YOUTUBE-KANAL?

Guckst du hier:

ICH WILL ZUM YOUTUBE-KANAL!

Quellen:

Bortz, J., & Schuster, C. (2017). Statistik für Human- und Sozialwissenschaftler. Berlin: Springer.

Field, A. (2018). Discovering Statistics using IBM SPSS Statistics. London: SAGE.

Sedlmeier, P., & Renkewitz, F. (2018). Forschungsmethoden und Statistik für Psychologen und Sozialwissenschaftler. München: Pearson.

Dichtefunktion einfach erklärt!

In der Psychologie und den meisten Sozialwissenschaften können wir immer nur Stichproben aus der interessierenden Grundgesamtheit ziehen und so gut wie nie alle in Betracht kommenden Personen befragen/testen/beobachten. Daher müssen wir uns mit den Ergebnissen aus einer Stichprobe begnügen und von diesen auf die dazugehörige Grundgesamtheit schließen.

Um das tun zu können, gibt es verschiedene Vorstellungen davon, wie Variablen wie z. B. Neugier, Offenheit für neue Erfahrungen oder Resilienz verteilt sein könnten, d. h. in welchem Bereich sich wohl die meisten Werte tummeln und wie wahrscheinlich es ist, dass eine Person aus der betreffenden Grundgesamtheit einen Wert hat, der in ein bestimmtes Intervall fällt.

Und genau dafür gibt es die Dichtefunktion: sie ist eine visuelle Darstellung der Auftretenswahrscheinlichkeiten von bestimmten Ausprägungen einer Variablen.

Inhaltsverzeichnis

Was ist eine Dichtefunktion?

In welchen Bereich der Statistik gehört sie?

Wie entsteht die Dichtefunktion?

Eigenschaften der Dichtefunktion

Steckbrief Dichtefunktion

Was ist eine Dichtefunktion?

Zunächst ein Beispiel: Angenommen, dich interessiert die Kompromissfähigkeit bei gewaltbereiten Jugendlichen auf einer Skala von 0 (= gar nicht vorhanden) bis 100 (= super stark ausgeprägt). Damit hättest du eine stetige, metrische Variable (auf Intervallskalenniveau).

"Stetig" bedeutet, dass zwischen zwei Merkmalsausprägungen THEORETISCH unendlich viele Werte liegen können, wenn man nur genau genug messen würde. Merk' dir vielleicht einfach, dass du bei stetigen Variablen potenziell immer ein Komma und unendlich viele Nachkomma-Stellen anhängen könntest. Also bei der Kompromissfähigkeit so was wie: 48,897120823546043745654...

Nun möchtest du womöglich wissen, wo sich die meisten Werte herumtreiben und wie wahrscheinlich es ist, dass ein Jugendlicher z. B. eine Kompromissfähigkeit zwischen 35 und 40 aufweist. Ersteres kannst du in der Dichtefunktion SEHEN, Letzteres mit der Verteilungsfunktion BERECHNEN.

Eine Dichtefunktion oder Wahrscheinlichkeitsdichte ist eine schicke visuelle Darstellung der Verteilung von stetigen Variablen. Sie zeigt dir, wie und wo sich die einzelnen Merkmalsausprägungen auf einer Skala verteilen und in welchem Bereich die meisten Werte auftreten.

Dort, wo sich die meisten Werte ballen, besteht auch die höchste Wahrscheinlichkeit dafür, dass eine zur interessierenden Grundgesamtheit gehörige (z. B. gewaltbereite Jugendliche), zufällig ausgewählte Person hier ihre Ausprägung hat. Bei der Normalverteilung ist das um den Mittelwert herum.

Hier siehst du die Dichtefunktion einer Normalverteilung zum Kompromissfähigkeits-Beispiel mit einem Mittelwert von 35 und einer Standardabweichung von 8. Der Bereich +/– eine Standardabweichung ist blau markiert – dort finden sich die meisten Werte. Daher ist auch die Wahrscheinlichkeit am höchsten, dass ein zufällig ausgewählter gewaltbereiter Jugendlicher hier seinen Wert hat, nämlich zwischen 27 und 43.

In welchen Bereich der Statistik gehört sie?

Die Dichtefunktion gehört in die Welt der Inferenzstatistik und dort in den Bereich des theoretischen Grundwissens.

Dieses Wissen brauchst du, um zu verstehen, wie die verschiedenen Verteilungen zustande kommen (z. B. t oder F), was man mit ihnen machen kann und wie man Wahrscheinlichkeiten berechnet.

Wie entsteht die Dichtefunktion?

Stell' dir vor, man würde zur Kompromissfähigkeit von gewaltbereiten Jugendlichen unendlich viele Untersuchungen machen und immer wieder Stichproben aus derselben Population ziehen.

Wenn man dann bei jeder dieser Untersuchungen z. B. den Mittelwert berechnen und diesen auf der oben genannten Skala zwischen 0 und 100 mit einem Strich aufzeichnen würde, bekäme man (sehr vereinfacht gesagt) mit der Zeit aus ganz, ganz vielen Strichen eine Fläche. Dort, wo die Werte besonders oft hinfallen, wo also Ballungen entstehen, häufen sich die Striche, werden länger und es entsteht eine Art Hügel oder Kurve.

Diese Kurve bzw. Dichtefunktion zeigt nun, an welcher Stelle sich die meisten Werte ansammeln und wie wahrscheinlich Merkmalsausprägungen in bestimmten Bereichen sind. Wo die Kurve am höchsten ist, ist auch die Wahrscheinlichkeit am höchsten, dass jemand dort seine Merkmalsausprägung hat.

Die Dichtefunktion muss jedoch nicht immer wie Schlange-frisst-Elefant aussehen.

Hier siehst du ein Beispiel der Dichtefunktion einer F-Verteilung – das ist die Verteilung, die du z. B. für die Varianzanalyse und Regression brauchst:

Eigenschaften der Dichtefunktion

Die Dichtefunktion ist eine sog. Wahrscheinlichkeitsdichte und kann genauso wie Wahrscheinlichkeiten nur positive Werte annehmen. Diese liegen immer zwischen 0 und 1 (das erste Axiom der Wahrscheinlichkeit).
Das bedeutet, dass die Gesamtfläche unter der Kurve immer den Wert p = 1 oder 100% hat (p steht für Wahrscheinlichkeit).
Anders ausgedrückt: die Wahrscheinlichkeit dafür, in einer Stichprobe einen Wert zu erheben, der IRGENDWO in dem Bereich unterhalb der Kurve liegt, ist 100% oder 1.
Die Wahrscheinlichkeit dafür, dass ein Wert in einen bestimmten Bereich unterhalb der Kurve fällt, also in ein bestimmtes Intervall, liegt irgendwo zwischen 0 und 1. Dies lässt sich dann mit der Verteilungsfunktion mithilfe wilder Integral-Rechnungen ermitteln.
Die Wahrscheinlichkeit für einen ganz bestimmten (!) Wert ist gleich 0. Das liegt daran, dass es ja bei metrischen Variablen POTENZIELL unendlich viele Ausprägungsmöglichkeiten gibt. Und da sich Wahrscheinlichkeiten immer zu 1 aufsummieren, funktioniert das bei unendlich vielen Werten nicht. Denn die Wahrscheinlichkeiten für diese unendlich vielen Merkmalsausprägungen müssten sich ja auch zu 1 aufsummieren lassen, was jedoch nicht geht.

Zum Abschluss noch ein kleiner Steckbrief:

Steckbrief Dichtefunktion

Wird auch Wahrscheinlichkeitsdichte genannt
Nur für stetige Variablen möglich! Für diskrete Variablen gibt es die Wahrscheinlichkeitsfunktion
Visuelle Darstellung von Auftretenswahrscheinlichkeiten
Zeigt, an welcher Stelle sich die meisten Werte ansammeln und wie wahrscheinlich Merkmalsausprägungen in bestimmten Bereichen sind
Gehört zum Basiswissen für die schließende oder Inferenzstatistik
Kann immer nur positive Werte zwischen 0 und 1 annehmen
Die Wahrscheinlichkeiten für Werte in einem bestimmten Intervall werden mit der Integralrechnung ermittelt
Die Wahrscheinlichkeit für einen ganz bestimmten Wert = 0

KENNST DU SCHON MEINEN YOUTUBE-KANAL?

Guckst du hier:

ICH WILL ZUM YOUTUBE-KANAL!

Quellen:

Bortz, J., & Schuster, C. (2017). Statistik für Human- und Sozialwissenschaftler. Berlin: Springer.

Field, A. (2018). Discovering Statistics using IBM SPSS Statistics. London: SAGE.

Sedlmeier, P., & Renkewitz, F. (2018). Forschungsmethoden und Statistik für Psychologen und Sozialwissenschaftler. München: Pearson.

Chi-Quadrat-Test auf Unabhängigkeit einfach erklärt!

Vermutlich wolltest du immer schon mal wissen, ob es einen Zusammenhang zwischen dem Geschlecht und der Wahl der Dating-App gibt. Nein? Vielleicht etwas Ähnliches? Wenn ja, hat das Warten nun ein Ende, denn wenn du tapfer weiterliest, werde ich dich in die Geheimnisse des Chi-Quadrat-Tests auf Unabhängigkeit einweihen – derjenigen Methode, mit der du herausfinden kannst, ob zwischen zwei nominalskalierten Merkmalen ein Zusammenhang besteht.

Inhaltsverzeichnis

Was ist der Chi-Quadrat-Test auf Unabhängigkeit?

In welchen Bereich der Statistik gehört er?

Was sagt der Chi-Quadrat-Test aus?

Chi-Quadrat-Test berechnen

Chi-Quadrat-Test mit SPSS

Steckbrief Chi-Quadrat-Test

Was ist der Chi-Quadrat-Test auf Unabhängigkeit?

Chi-Quadrat klingt ja irgendwie ein wenig fernöstlich (= potenzierte Lebensenergie?), hat damit allerdings eher wenig zu tun. Dafür umso mehr mit einem statistischen Verfahren, bei dem überprüft wird, ob zwei nominalskalierte, kategoriale Variablen wie z. B. Geschlecht, Nationalität, Studienfach, Wahl der Automarke, gewählte Partei etc. zusammenhängen.

Der Begriff "Unabhängigkeit" bedeutet, dass kein Zusammenhang zwischen den Variablen besteht!

Das ist auch die Nullhypothese, die dieser Test überprüft, beispielsweise: "Es besteht kein Zusammenhang zwischen einer bestimmten Persönlichkeitsstörung und dem gewählten Studienfach".

Anders formuliert: Die Wahl des Studienfaches ist unabhängig von einer eventuell vorhandenen Persönlichkeitsstörung. Oder so: Die vorliegende Persönlichkeitsstörung hat keinen Einfluss auf die Wahl des Studienfaches (und umgekehrt).

Möglich ist auch, den Test mit Variablen durchzuführen, die auf einer höheren Skala liegen. In diesem Fall müsste man die Variablen dann quasi "downgraden" und in Kategorien verpacken (was jedoch immer mit Informationsverlust verbunden ist).

In welchen Bereich der Statistik gehört er?

Der Chi-Quadrat-Test gehört in die Welt der Inferenzstatistik, dient also dazu, von den Daten einer Stichprobe auf die dazugehörige Grundgesamtheit zu schließen. Der Test basiert auf dem Chi-Quadrat-Koeffizienten, den du bereits aus der deskriptiven Statistik kennen müsstest.

Zudem gehört er in den Bereich der Zusammenhangshypothesen.

Was sagt der Chi-Quadrat-Test aus?

Der Chi-Quadrat-Test sagt aus, ob ein Zusammenhang zwischen zwei nominalskalierten Variablen besteht und wenn ja, wie stark dieser ist. Die Berechnung der dazugehörigen Effektgröße wird hier jedoch nicht dargestellt.

Als grobe Daumenregel gilt zunächst einmal: kleiner Wert = geringer Zusammenhang; großer Wert = starker Zusammenhang.

Hier gibt es leider keine Normierung, daher kann der Chi-Quadrat-Wert, der bei deiner Berechnung herauskommt, potenziell beliebig groß werden – er ist jedoch immer positiv. Das macht die Interpretation ein wenig schwierig...

Man kann jedoch einen Maximalwert berechnen und erhält dadurch einen gewissen Anhaltspunkt. Das zeige ich dir nachher bei der Berechnung.

Zudem kannst du bei einem signifikanten Ergebnis die Effektstärke Klein Omega oder Cramérs Phi berechnen.

Chi-Quadrat-Test berechnen

Kommen wir für die Berechnung zum Eingangsbeispiel zurück:

Gibt es einen Zusammenhang zwischen dem Geschlecht und der Wahl einer Dating-App?

Um das Beispiel möglichst einfach zu halten, definieren wir die Ausprägungen von Geschlecht ganz old school als weiblich und männlich. Die Dating-Apps oder Single-Börsen sind Parship und Tinder (selbstverständlich ist der Chi-Quadrat-Unabhägigkeitstest auch mit mehr als nur zwei Ausprägungen pro Merkmal anwendbar!).

Dazu wurden jeweils 20 Frauen und Männer befragt.

Hier ist dazu die sogenannte Kreuz- oder Kontingenztabelle:

Grundprinzip der Berechnung

Um die Frage nach dem Zusammenhang zu überprüfen, wird berechnet, wie häufig eine bestimmte Merkmalskombination (also z. B. Frau und Parship) vorliegen müsste, wenn kein Zusammenhang bestünde – das ist die erwartete Häufigkeit.

Diese erwartete Häufigkeit wird dann mit den tatsächlich vorhandenen Häufigkeiten in der Kreuztabelle verglichen.

GIBT ES (SIGNIFIKANTE) ABWEICHUNGEN ZWISCHEN DEN THEORETISCH ERWARTETEN UND DEN TATSÄCHLICH BEOBACHTETEN HÄUFIGKEITEN, LIEGT EIN ZUSAMMENHANG VOR!

Dies ist die Formel für die Berechnung des Chi-Quadrat-Koeffizienten (das x-Quadrat ist die mathematische Notation für Chi-Quadrat!):

Die beobachtete Häufigkeit ist das, was du in der Kreuztabelle siehst.

Wie bekommst du nun die erwartete Häufigkeit?

Dazu multiplizierst du für jede Zelle jeweils die zu dieser Merkmalskombination dazugehörige Zeilensumme mit der dazugehörigen Spaltensumme und teilst das Ergebnis dann durch das Gesamt-N:

Um herauszufinden, wieviele Frauen Parship nutzen würden, wenn es keinen Zusammenhang zwischen dem Geschlecht und der Wahl der Dating-App gäbe, rechnest du:

Weiblich / Parship: (Zeilensumme 17 x Spaltensumme 20) : 40 = 8,5

Hier sehen wir bereits, dass mehr Frauen als erwartet Parship wählen, nämlich 14.

Prüfen wir jetzt noch die anderen Zellen:

Weiblich / Tinder: (23 x 20) : 40 = 11.5 – beobachtet wurden jedoch 6, also weniger

Männlich / Parship: (17 x 20) : 40 = 8.5 – beobachtet wurden jedoch 3, also deutlich weniger!

Männlich / Tinder: (23 x 20) : 40 = 11.5 – beobachtet wurden jedoch 17, also deutlich mehr!

Nächster Schritt:

Alles in die Formel einsetzen und sich den Wolf rechnen – das Ergebnis ist dann der Chi-Quadrat-Koeffizient:

Und was sagt uns das jetzt?

Noch nicht so viel... Immerhin können wir ausrechnen, wie groß der Chi-Quadrat-Wert /-Koeffizent in unserem Beispiel maximal werden könnte:

Wertebereich Chi-Quadrat-Koeffizient

Hier kannst du sehen, dass der Chi-Quadrat-Wert nicht negativ wird.

Der maximal mögliche Wert wird berechnet, indem du die Stichprobengröße mit (M - 1) multiplizierst. Dabei ist M der kleinere Wert der Anzahl von Zeilen und Spalten. Dazu ein Beispiel:

Angenommen, wir hätten bei Geschlecht noch "divers" hinzugenommen, dann hätten wir drei Spalten für das Geschlecht und zwei für die Dating-Apps gehabt. In diesem Fall wäre dann der kleinere Wert der Anzahl von Zeilen und Spalten die zwei, da es zwei Dating-Apps und drei Geschlechts-Ausprägungen geben würde.

Da wir in unserem Beispiel jeweils zwei Ausprägungen haben, ist es also einfach die zwei.

Somit wäre der maximal mögliche Wert hier:

40 x (2 - 1) = 40 (da sind wir mit unserem gefundenen Wert von 12.377 noch etwas davon entfernt).

Um das Ganze jetzt statistisch auf Signifikanz zu überprüfen, brauchen wir SPSS (oder eine Chi-Quadrat-Tabelle):

Chi-Quadrat-Test mit SPSS

Zur Erinnerung – die getestete Nullhypothese lautet: Es liegt KEIN Zusammenhang zwischen den Variablen vor!

Wenn du nun ein signifikantes Ergebnis erhältst (einen p-Wert kleiner 0,05), wird die Nullhypothese verworfen und die Alternativhypothese angenommen, die da lautet:

Es liegt ein signifikanter Zusammenhang zwischen den beiden Variablen vor.

Zur Vorgehensweise:

Ruf' zunächst deinen Datensatz auf (oder gib' selbst Daten ein).

Dann gehst du auf "Analysieren", "Deskriptive Statistiken", "Kreuztabellen". Im sich öffnenden Fenster klickst du die beiden nominalskalierten Variablen an, die dich interessieren, und ordnest sie den Zeilen oder Spalten zu. Es macht für das Ergebnis übrigens keinerlei Unterschied, welches Merkmal du den Zeilen oder Spalten zuordnest.

Jetzt klickst du auf das Kästchen "Statistiken" auf der rechten Seite und setzt bei "Chi-Quadrat" einen Haken, drückst auf "weiter" und dann auf "OK". Es erscheint der nachfolgende Output.

Ein weiteres Beispiel dazu findest du hier.

Nicht verwirren lassen – wie bei SPSS üblich, wird deutlich mehr ausgegeben als du brauchst...
Schau' in der ersten Zeile bei "Chi-Quadrat nach Pearson" und "Asymptotische Signifikanz" nach
Dort liest du den p-Wert ab und schaust, ob er unter ,05 liegt, was hier eindeutig der Fall ist
Daher besteht ein signifikanter Zusammenhang zwischen dem Geschlecht und der Wahl der Dating-App!
Zudem bitte immer die Fußnoten beachten: Wenn es Felder in der Kreuztabelle gibt, in denen erwartete Häufigkeiten unter 5 vorkommen, kann der Chi-Quadrat-Test zu einem ungenauen oder falschen p-Wert führen. In diesem Falle oder bei kleinen Stichproben bitte bei "Exakter Test nach Fisher" ablesen!
In welche Richtung der gefundene Zusammenhang geht, kannst du an der Kreuztabelle ablesen

Fazit für unsere Untersuchung:

Je mehr Mann, desto mehr Tinder – und je mehr Frau, desto mehr Parship... (caveat: Das ist eine sehr flapsige und keineswegs statistisch korrekte Interpretation!).

Oder so: Es gibt einen signifikanten Zusammenhang zwischen dem Geschlecht und der Wahl der Dating-App: Männer neigen eher zu Tinder, wohingegen Frauen Parship präferieren.

Zu guter Letzt noch ein kleiner Steckbrief:

Steckbrief Chi-Quadrat-Test

Prüft, ob zwischen zwei nominalskalierten Merkmalen ein Zusammenhang besteht
Kann auch bei höher skalierten Variablen angewendet werden, die dann "downgegradet" und in Kategorien verpackt werden
Vergleicht die bei Unabhängigkeit theoretisch erwarteten mit den tatsächlich in der Stichprobe gefundenen/beobachteten Häufigkeiten
Weichen die beobachteten Häufigkeiten deutlich von den erwarteten ab, liegt ein signifikanter Zusammenhang vor
Der Chi-Quadrat-Wert ist nicht normiert und kann potenziell beliebig groß werden
Mit SPSS (oder einer Tabelle) lässt sich überprüfen, ob der Zusammenhang signifikant ist
Bei signifikantem Ergebnis eine Effektstärke wie beispielsweise Klein Omega oder Cramérs Phi berechnen

Quellen (Als Amazon-Partnerin verdiene ich an qualifizierten Verkäufen):

Bortz, J., & Schuster, C. (2017). Statistik für Human- und Sozialwissenschaftler. Berlin: Springer.

Bühner, M., & Ziegler, M. (2017). Statistik für Psychologen und Sozialwissenschaftler. München: Pearson.

Field, A. (2018). Discovering Statistics using IBM SPSS Statistics. London: SAGE.

Sedlmeier, P., & Renkewitz, F. (2018). Forschungsmethoden und Statistik für Psychologen und Sozialwissenschaftler. München: Pearson.

Geschafft – Geht doch!

Wenn ich dir einen kleinen Vorschlag machen dürfte, würde ich sagen, du schnappst dir einen Datensatz (z. B. von Andy Field) oder erfindest selbst einen mit einer überschaubaren Anzahl von Werten, überlegst dir eine sinnvolle Fragestellung und übst gleich einmal die Anwendung – entweder per Hand und/oder mit SPSS.

Viel Erfolg!

Und natürlich nicht vergessen: Belohnen!

Statistik kann ja gerne mal ein wenig dröge sein.

Daher sollte man sich's danach oder währenddessen unbedingt gut gehen lassen:

Foto von Maddi Bazzocco auf Unsplash

Effektstärke d (Cohens d) einfach erklärt!

Cohens d zeigt dir, wie groß ein gefundener Effekt bei Mittelwertsunterschieden ist. Das wäre z. B. eine Fragestellung wie: "Unterscheiden sich Frauen und Männer in ihrem Shopping-Durchhaltevermögen?". Wenn du diese Studie machen würdest, würdest du zunächst einen t-Test für unabhängige Stichproben durchführen und dann schauen, ob du ein signifikantes Ergebnis erhältst. Anschließend stellt sich dann die Frage, wie groß der gefundene Mittelwertsunterschied zwischen den beiden Gruppen ist und in welche Richtung er geht. Wobei wir hier vermutlich auch ohne Daten so unsere Vermutungen hätten....

Im Folgenden zeige ich dir, wie du (meist nach Durchführung eines Signifikanztests – Stichwort: p-Wert) durch die Berechnung von Cohens d eine Aussage über die praktische Relevanz des gefundenen Effekts machen kannst.

Da es für dieses Effektstärkemaß verschiedene Varianten gibt (man mag es in der Statistik ja gerne etwas kompliziert), dreht sich dieser Artikel ausschließlich um Cohens d zum Unterschied zweier Mittelwerte aus unabhängigen Stichproben. Der Begriff "unabhängige Stichproben" meint, dass bei allen Proband*innen nur einmal der interessierende Wert erhoben wurde.

Inhaltsverzeichnis

Was sind Effektstärken?

In welchen Bereich der Statistik gehören sie?

Was sagt Cohens d aus?

Berechnung Cohens d

Konventionen für die Interpretation

Cohens d mit SPSS & Online-Rechnern

Steckbrief Cohens d

Was sind Effektstärken?

Effektstärken bzw. Effektstärkemaße zeigen, wie stark ein in einer Studie beobachteter Effekt ist.

Je nach Inhalt der Untersuchung verwendet man unterschiedliche Effektstärkemaße. Diese werden in zwei Gruppen eingeteilt: Abstandsmaße und Zusammenhangsmaße.

Erstere zeigen meist die Größe der Abstände zweier Mittelwerte in Standardabweichungs-Einheiten an, während Letztere gewöhnlich Variationen des Korrelationskoeffizienten r nach Bravais-Pearson sind. Schickerweise lassen sich beide Gruppen ineinander überführen!

In welchen Bereich der Statistik gehören sie?

Die Effektstärken gehören in die Welt der schließenden oder Inferenzstatistik, können jedoch auch deskriptivstatisch verwendet werden – also nur zur Beschreibung dessen, was bei bestimmten Stichproben vorgefunden wird, ohne auf die dazugehörige Grundgesamtheit schließen zu wollen.

Im Bereich der Inferenzstatistik sollten sie zusätzlich zur Angabe des Ergebnisses eines Signifikanztests mit angegeben werden.

Was sagt Cohens d aus?

Cohens d ist eines der am häufigsten in der Statistik verwendeten Effektstärkemaße und beschreibt, wie stark sich die Mittelwerte zweier Stichproben unterscheiden.

Da Cohens d ein standardisiertes Abstandsmaß ist, ist es unerheblich, mit welchen Messinstrumenten die abhängige Variable erhoben wurde. Denn durch die Standardisierung werden evtl. mit verschiedenen Messinstrumenten gemessene Mittelwerte auf eine neue, gemeinsame dimensionslose Einheit gebracht und dadurch direkt vergleichbar.

Ein weiterer Vorteil ist, dass Cohens d im Gegensatz zum p-Wert nicht von der Stichprobengröße abhängt.

Grafisch dargestellt bedeutet der Mittelwertsunterschied, wie weit die beiden Mittelwerte auf der x-Achse auseinander liegen. Je näher, desto kleiner d – und je weiter auseinander, desto größer d und somit der gefundene Effekt.

Guckst du – hier liegen die Mittelwerte relativ weit auseinander, so dass ein mittlerer bis großer Effekt vorliegt. Ob dieser Effekt groß genug ist, um statistisch signifikant zu sein, muss man jedoch berechnen.

Berechnung Cohens d

Hier ist die Formel, um den standardisierten Mittelwertsunterschied bei zwei unabhängigen Stichproben zu berechnen.

Wir machen das jetzt zur oben erwähnten Fragestellung zum Unterschied des Shopping-Durchhaltevermögens von Frauen und Männern. Das Shopping-Durchhaltevermögen wird auf einer Skala von 0 (= gar nicht vorhanden) bis 100 (= stolze*r Preisträger*in der platinfarbenen Einkaufstasche) erhoben.

Die unten abgebildete Formel besteht im Zähler aus dem Abstand zwischen den beiden Mittelwerten, der dann anhand der gemeinsamen Streuung im Nenner relativiert und somit standardisiert wird. Da gewöhnlich von Stichproben-Mittelwerten ("x quer") auf die Erwartungswerte in der Population ("mü") geschlossen wird, verwendet man in der Praxis den zweiten, rechten Teil der Formel:

Angenommen, wir hätten aus unseren Daten Folgendes errechnet:

- für die Frauen (Gruppe A) einen Mittelwert von 65.3 mit einer Standardabweichung von 4.5

- für die Männer (Gruppe B) einen Mittelwert von 59.6 mit einer Standardabweichung von 3.9

Die Mittelwerte für den Zähler haben wir nun schon, jetzt fehlt uns nur noch die gemeinsame Streuung für den Nenner. Dafür gibt es zwei Varianten:

Wenn die Stichprobengröße bei beiden Gruppen gleich ist, verwendest du die folgende Formel für die Berechnung der gemeinsamen Streuung:

Wenn wir beispielsweise eine Stichprobengröße von 60 Personen in beiden Stichproben (= gleiche Anzahl von Personen in jeder Gruppe) haben, sieht die obige Formel nun so aus:

Jetzt können wir alle Werte in die oberste Gleichung einsetzen und erhalten d:

Gemäß den Konventionen von Cohen (s. u.) wäre das ein ausgesprochen starker und praktisch bedeutsamer Mittelwertsunterschied!

Ist hingegen die Stichprobengröße ungleich, nimmst du diese schöne Formel für die gemeinsame Streuung:

Bei Stichprobengrößen von 58 Frauen (Gruppe A) und 51 Männern (Gruppe B) sieht das dann so aus:

In die Ursprungsformel eingesetzt:

FAZIT:

In diesem Fall bleibt die Aussage gleich, da sich durch die unterschiedlichen Stichprobengrößen nichts verändert hat (dies ist jedoch nicht immer so).

Es liegt hier also ein ausgesprochen starker Mittelwertsunterschied vor, d. h. Männer und Frauen unterscheiden sich sehr stark in ihrem Shopping-Durchhaltevermögen (wer hätte das gedacht!). Die Frauen sind um 1.35 Standardabweichungen durchhaltefähiger als die Männer!

Brauchst du hilfe beim lernen von statistik?

Dann komm' zu statistik-gym, dem Online-Fitnessstudio für Statistik,

das dich fit für die Prüfung macht!

Eine Mitgliedschaft wie bei Netflix oder Spotify, nur eben für Statistik im Bachelor,

die dir hilft, dieses Fach endlich zu verstehen & die Prüfung zu meistern!

Darin bekommst du:

Eine monatlich wachsende Bibliothek von Videos & Audios
Live Frage- & Antwort-Sessions
Eine Roadmap, mit der du zielsicher durch den Dschungel der Statistik geführt wirst
Alles rund um Mindset, Motivation & Lerntechniken
Downloads wie Übungsblätter, Steckbriefe & Probeklausuren
Webinare / live Teachings
Du kannst jederzeit in der Community Fragen stellen & dich mit anderen austauschen!

Und dann macht Statistik vielleicht sogar Spaß!

Klingt gut? Dann klick' hier:

ich will zu statistik-gym!

Konventionen für die Interpretation

Praktischerweise gibt es für die Interpretation der Mittelwertsunterschiede von J. Cohen (1988) vorgeschlagene Konventionen, welche als grober Anhaltspunkt zu verstehen sind:

|d| = 0.2 kleiner Effekt
|d| = 0.5 mittlerer Effekt
|d| = 0.8 großer Effekt

Die Striche um das d herum sind Betragstriche, was bedeutet, dass der Wert z. B. –0.2 oder +0.2 sein kann. Cohens d kann also auch negativ werden.

Da es sich hierbei um Konventionen bzw. Orientierungspunkte handelt, sollte man die in einem Forschungsbereich typischen Effekte bei der Interpretation mit einbeziehen. Schau' dir also vor der finalen Einschätzung der Stärke des gefundenen Effekts verschiedenen Studien zu deinem Thema an, um ein Gefühl dafür zu bekommen, was in dem jeweiligen Feld als "kleiner", "mittlerer" oder "großer" Effekt bezeichnet werden kann.

Cohens d mit SPSS & Online-Rechnern

SPSS spuckt d erst ab Version 27 mit aus.

Falls du eine niedrigere Version hast oder gar nicht mit SPSS arbeitest, gibt's Psychometrica, eine wunderbare und sehr hilfreiche Seite zur Berechnung diverser statistischer Kennzahlen.

Nun Zum Abschluss noch ein Steckbrief:

Steckbrief Cohens d

Abstandsmaß für die Stärke/Größe von Mittelwertsunterschieden
Drückt den Unterschied in Standardabweichungs-Einheiten aus
Daher auch geeignet für abhängige Variablen, die mit verschiedenen Messinstrumenten erhoben wurden
Aufgrund der Berechnung von Mittelwerten nur bei metrischen Skalen anwendbar!
Cohens Konventionen zur Stärke des Effekts sind nur als grobe Richtlinie zu verstehen – wichtig, immer die im jeweiligen Forschungsbereich "typischen" Effekte zu recherchieren
Kann ab Version 27 direkt mit SPSS und mit Online-Rechnern wie Psychometrica oder der Freeware G*Power berechnet werden

Geschafft – Respekt!

Wenn du einen Beispiel-Datensatz zur Hand hast (z. B. von Andy Field), dann versuch' dich doch gleich mal an der Berechnung von d und überprüf' deine Ergebnisse bei Psychometrica!

Und jetzt: fette Belohnen!

Statistik ist ja gemeinhin nicht das allerflauschigste Fach.

Also sollten wir es uns zumindest beim und nach dem Lernen gut gehen lassen...

Foto von Serafima Lazarenko auf Unsplash

Quellen (Als Amazon-Partnerin verdiene ich an qualifizierten Verkäufen):

Bühner, M., & Ziegler, M. (2017). Statistik für Psychologen und Sozialwissenschaftler. München: Pearson.

Sedlmeier, P., & Renkewitz, F. (2018). Forschungsmethoden und Statistik für Psychologen und Sozialwissenschaftler. München: Pearson.

Field, A. (2018). Discovering Statistics using IBM SPSS Statistics. London: SAGE.

Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed). Hillsdale, N.J: L. Erlbaum Associates.

Ellis, P. D. (2010). The Essential Guide to Effect Sizes: Statistical Power, Meta-Analysis, and the Interpretation of Research Results. Cambridge: Cambridge University Press.

Mythos und Realität des p-Werts…p-Wert einfach erklärt!

Mythen und Märchen unterschiedlichster Couleur ranken sich um den p-Wert. Manche sagen, das habe irgendwie was mit Wahrscheinlichkeit zu tun, andere behaupten, das sei das, was in der Spalte "Sig." bei SPSS stünde, und wiederum andere meinen, der p-Wert sei die Wahrscheinlichkeit für die Nullhypothese (oder war's die Alternativhypothese?).

Um ein wenig Licht ins sagenumwobene Dunkel zu bringen, folgt hier zunächst die Kurzversion und anschließend eine ausführlichere Erklärung.

Inhaltsverzeichnis

Die Kurzversion – quick & dirty

Grundsätzliches, um dich thematisch einzunorden

Die Basis des p-Werts: Verteilungen

Der p-Wert am Beispiel der Varianzanalyse

Was hat der p-Wert mit der Signifikanz zu tun?

Beispiel für den p-Wert bei SPSS: Korrelation

Beispiel für den p-Wert bei SPSS: F-Test

Zusammenfassung

Die Kurzversion – quick & dirty

Der p-Wert zeigt an, wie wahrscheinlich dein Ergebnis ist, WENN DIE NULLHYPOTHESE STIMMEN WÜRDE.

Oder so: Der p-Wert ist eine BEDINGTE WAHRSCHEINLICHKEIT – nämlich die Wahrscheinlichkeit für dein spezielles Ergebnis (Mittelwert, Korrelation, F-Test etc.), unter der bedingung, dass die NULLHYPOTHESE Gilt.

Vielleicht auch so: Wenn die Nullhypothese stimmen würde – wie wahrscheinlich ist dann dein Ergebnis?

Für die weitere Auswertung gilt gemäß der meist (noch) geltenden Konvention:

Ist der p-Wert, den man bei SPSS unter "Sig." ablesen kann, kleiner als .05 (p < 0.05) – ist dein Ergebnis also so unwahrscheinlich, dass es kein Zufall mehr sein kann – , so liegt ein signifikantes Ergebnis vor und die Nullhypothese wird verworfen.

CAVEAT: Ich setze in diesem Artikel Wissen zum Hypothesentesten und zu Verteilungen voraus! Falls du damit noch nicht vertraut bist, hast du wahrscheinlich mehr davon, wenn du dich erst mal ein wenig dazu schlau machst.

Grundsätzliches, um dich thematisch einzunorden

Wir befinden uns in der Welt der inferenz- oder schließenden Statistik
Hier im Speziellen in der WELT DES HYPOTHESENTESTENS
Beim Hypothesentesten geht es meist um Zusammenhänge, Unterschiede oder Veränderungen über die Zeit hinweg
Ganz wichtig: GETESTET WIrd immer die Gültigkeit der Nullhypothese!
Wir haben eine Studie durchgeführt und wollen jetzt wissen, ob unsere Ergebnisse signifikant sind
Dies können wir am p-Wert ablesen!

Die Basis des p-Werts: Verteilungen

Wenn du Hypothesentests durchführst, tust du das immer vor dem Hintergrund einer bestimmten Verteilung.

Das kann z. B. die Normal- bzw. Standardnormalverteilung sein, oder aber die F-, Chi-Quadrat- oder t-Verteilung – jeweils abhängig vom Inhalt deiner Hypothese. Eine Verteilung enthält 100% aller Werte – oder in Wahrscheinlichkeiten ausgedrückt: die Fläche unter der Kurve ist stets 1.

Du testest immer ein Modell: eine Vorstellung davon, wie die Daten unter Gültigkeit der Nullhypothese verteilt sind. Wobei die Nullhypothese besagt, dass der postulierte Unterschied oder Zusammenhang NICHT existiert. Beim Hypothesentesten geht es also darum, zu überprüfen, ob die Nullhypothese nach wie vor gilt – oder aber verworfen wird.

Als Ergebnis deines Hypothesentests erhältst du einen Wert (z. B. einen t-, z- oder F-Wert), der in der dazugehörigen Verteilung liegt.

Die Wahrscheinlichkeit dafür, dass dein Ergebnis-Wert genau an diesen bestimmten Punkt in der jeweiligen Verteilung fällt (wenn die Nullhypothese gilt), ist der p-Wert.

Beispiel t-Test:

Du führst eine Untersuchung zur Frage durch, ob Männer geduldiger sind als Frauen. Dann wäre die Nullhypothese: "Frauen und Männer unterscheiden sich nicht in ihrer Geduld.", wohingegen deine Alternativhypothese lautet: "Männer sind geduldiger als Frauen." (rechtsseitiger Test).

Da die Varianz unbekannt ist und es um Mittelwerts-Unterschiede geht, führst du einen t-Test durch und lässt 5% Irrtumswahrscheinlichkeit zu (α = 0.05). Nun erhältst du bei deiner Auswertung zum Beispiel einen t-Wert von 1.83.

Dessen Wahrscheinlichkeit, genau an diesen Punkt in der t-Verteilung zu fallen, sofern die Nullhypothese gilt, liegt bei 0.03 – und das ist der p-Wert, also in diesem Falle eine Wahrscheinlichkeit von 0.03 oder in Prozenten ausgedrückt: 3% (sehr unwahrscheinlich). Somit hast du ein signifikantes Ergebnis, verwirfst die Nullhypothese und nimmst deine Alternativhypothese mit 5%iger Irrtumswahrscheinlichkeit an.

Weitere Verteilungen (als kleine Erinnerungsstütze):

Der p-Wert am Beispiel der Varianzanalyse

Bei einer varianzanalytischen Fragestellung wie z. B. "Wirken sich Gestalttherapie, Psychoanalyse und Verhaltenstherapie unterschiedlich auf die Lebensqualität der Patient*innen aus?" verwendest du die F-Verteilung. Als Ergebnis deiner Auswertungen (ANOVA-Tabelle) erhältst du einen F-Wert, der in der F-Verteilung liegt.

Dieser Wert fällt, wie oben beschrieben, in einen bestimmten Bereich der F-Verteilung, kommt also irgendwo unter der "Kurve" (= Dichtefunktion) zu liegen (in der Grafik stellt jetzt die weiße Fläche die äußeren 5% dar – der F-Wert ist rot abgetragen).

Du bekommst also wieder zunächst den Ergebnis-F-Wert – und dann die dazugehörige Wahrscheinlichkeit für diesen F-Wert, falls die Nullhypothese stimmt: den p-Wert.

Dieser p-Wert von p = 0.041 bedeutet nichts anderes als: Das Ergebnis deiner Untersuchung fällt an den Punkt, an dem die äußeren 4.1% der Verteilung beginnen.

Anders ausgedrückt: Die Wahrscheinlichkeit für dein spezielles Ergebnis (deinen F-Wert) oder ein noch kleineres Ergebnis liegt bei 0.041 (im Alltagsjargon: bei 4.1%), wenn die Nullhypothese tatsächlich zutrifft – ist also sehr gering.

Bitte beachten:

Ich gehe hier aus Einfachheitsgründen vom üblichen Signifikanzniveau von α = 0.05 aus, also den äußeren 5% einer Verteilung.

Dies sollte jedoch bei jeder Untersuchung individuell abgewogen und festgesetzt werden!

Was hat der p-Wert mit der Signifikanz zu tun?

Liegt der p-Wert in den äußeren 5% einer Verteilung (p < 0.05), so liegt ein signifikantes Ergebnis vor!

Die äußeren 5% können sich je nach Hypothese rechts, links oder beidseitig befinden – in letzterem Fall jeweils in den äußeren 2.5% auf beiden Seiten (s. Abbildung Standardnormalverteilung).

Erhält man in einer Studie ein Ergebnis bzw. einen Wert, der in die äußeren 5% einer Verteilung hineinfällt, so ist dieses Ergebnis so unwahrscheinlich, dass man sagt:

das kann kein Zufall mehr sein!

Eine solche starke Abweichung vom bisher Bekannten muss ein signifikantes Ergebnis sein!

WIE unwahrscheinlich (oder wahrscheinlich) dieses Ergebnis genau ist, sagt der p-Wert aus.

Daher lässt sich an der Höhe des p-Werts die Signifikanz ablesen:

Ist der p-Wert kleiner als 0.05, so liegt ein signifikantes (weil sehr unwahrscheinliches) Ergebnis vor.

In diesem Falle verwirfst du die Nullhypothese und nimmst deine Alternativhypothese an. Wenn dein p-Wert größer als 0.05 ist, verwirfst du deine Alternativhypothese und behältst die Nullhypothese bei.

Beispiel für den p-Wert bei SPSS: Korrelation

Der folgende Datensatz ist von Andy Field (dessen Arbeit ich sehr schätze). Du kannst dir hier ganz viele bunte Datensätze von ihm holen und damit üben.

Fragestellung in diesem Datensatz:

Kann der Verkauf von Alben einer Band (abhängige Variable bzw. Kriterium) aus den folgenden drei Variablen ( Prädiktoren) vorhergesagt werden:

Werbe-Budget
Häufigkeit, mit der die Lieder der Band im Radio gespielt werden
Band-Image

Als Methode kommt hier die Regressionsanalyse zum Einsatz, da es um Vorhersagen geht.

Im ersten Output siehst du im oberen Drittel die Korrelationen (Zusammenhänge), welche die Grundvoraussetzung für die Berechnung einer Regression darstellen (Korrelationskoeffizienten r nach Bravais-Pearson = Produkt-Moment-Korrelation).

Kleiner Hinweis: In diesen Tabellen sind die Informationen jedes Abschnitts immer doppelt vorhanden – jeweils einmal oberhalb und unterhalb einer gedachten Diagonalen von links oben nach rechts unten.

Hier ist die Nullhypothese, dass es keinen Zusammenhang zwischen jeweils zwei Variablen gibt, also zwischen z. B. verkauften Alben und Band Image, zwischen Band Image und Werbe-Budget etc..

Im mittleren Bereich (bei "Sig.") findest du dazu die Auswertung (p-Werte): Sind die Korrelationen statistisch signifikant?

1. Zeile – Album Sales:

Hier kannst du an den aufgeführten p-Werten ablesen, dass die Anzahl an verkauften Alben signifikant mit den drei Prädiktoren korreliert: dreimal ",000" in der Zeile "Album sales".

Hinweis: Bei SPSS werden gewöhnlich immer nur die ersten drei Nachkommastellen angegeben. Irgendwann kommt dann vermutlich auch mal eine andere Zahl als Null, z. B. so was wie 0.00072134.

Die p-Werte sagen uns, dass die Wahrscheinlichkeit dafür, ein solches Ergebnis zu erhalten, wenn die Nullhypothese stimmen würde, unterhalb von 0.000% liegt. Somit ist das Ergebnis unter Gültigkeit der Nullhypothese extrem unwahrscheinlich.

Und was machen wir nun?

Richtig, wir verwerfen die Nullhypothese und nehmen die Alternativhypothese an, die da heißt:

Es gibt einen hochsignifikanten Zusammenhang (da p = 0.000) zwischen der Anzahl an verkauften Alben und jedem der drei Prädiktoren!

2. Zeile: Advertising budget:

Hier sind beide p-Werte für den Zusammenhang zwischen dem Werbe-Budget und der Anzahl an im Radio gespielten Liedern sowie dem Band-Image auf dem 5%-Niveau NICHT signifikant, da größer als p = 0.05.

Es gibt also weder einen signifikanten Zusammenhang zwischen dem Werbe-Budget und der Anzahl an im Radio gespielten Liedern noch zwischen dem Werbe-Budget und dem Band-Image. Beide dazugehörigen Nullhypothesen werden beibehalten.

3. Zeile: No. of plays on radio:

Der p-Wert von .005 zeigt einen hochsignifikanten Zusammenhang zwischen der Anzahl an im Radio gespielten Liedern und dem Band-Image.

Also verwerfen wir die Nullhypothese und nehmen die Alternativhypothese an:

Es gibt einen hochsignifikanten Zusammenhang (da p = 0.005) zwischen der Anzahl an im Radio gespielten Liedern und dem Band-Image!

Beispiel für den p-Wert bei SPSS: F-Test

Und weiter geht's: wir sind immer noch bei dem Beispiel von oben.

Im nächsten Schritt wird mit dem F-Test der Varianzanalyse überprüft, ob das Modell mit den drei Prädiktoren insgesamt etwas taugt.

Du denkst dir jetzt wahrscheinlich: "Wieso Varianzanalyse – ich dachte, wir machen eine Regression?!"

Ich gebe zu, dass das etwas verwirrend ist, aber das liegt daran, dass die Regressions- und Varianzanalyse verwandt sind und demselben mathematischen Modell entstammen, dem Allgemeinen Linearen Modell, für die Eingeweihten kurz: ALM.

Aus diesem Grund wird bei SPSS bei jeder Regression immer zunächst der F-Test der Varianzanalyse ausgegeben. Dieser wird auch "Globaler F-Test " oder "Omnibus-Test" genannt und prüft, ob das Gesamt-Modell signifikant ist.

Die Nullhypothese lautet: Keiner der Prädiktoren hat einen Einfluss auf das Kriterium, also auf die Anzahl an verkauften Alben.

Hier sehen wir in der ersten Zeile bei "Regression" einen sehr hohen F-Wert (129.498) und den dazugehörigen p-Wert von .000.

Wir haben somit wieder ein hochsignifikantes Ergebnis und können davon ausgehen, dass das Regressions-Modell mit den drei Prädiktoren insgesamt etwas taugt.

Also verwerfen wir die Nullhypothese und nehmen die Alternativhypothese an, die in diesem Falle lautet:

Mindestens einer der Prädiktoren hat einen Einfluss auf die Anzahl an verkauften Alben!

Welcher das ist bzw. welche das sind, sieht man dann in der Ergebnistabelle mit dem Namen "Koeffizienten", die hier jedoch nicht mehr aufgeführt ist. Falls dich das interessiert, kannst du dir einfach diesen Datensatz holen (oder einen anderen Regressions-tauglichen) und die Tabelle von SPSS ausspucken lassen.

Zusammenfassung

Du erhältst als Ergebnis deiner Untersuchung (mindestens) einen Wert (z, t, F etc.).
Dieser fällt an einen bestimmten Punkt in der dazugehörigen Verteilung.
Jedem Punkt in der Verteilung ist eine bestimmte Wahrscheinlichkeit zugeordnet.
Nun liest du in den Ergebnistabellen (z. B. von SPSS) bei "Sig." die Wahrscheinlichkeit dafür ab, dass dein Ergebnis-Wert genau an diesen Punkt der Verteilung fällt, wenn die Nullhypothese gilt. Dies ist der p-Wert.
An der Höhe des p-Werts kannst du sehen, ob dein Ergebnis signifikant ist (das wäre ein p < 0.05).
Jetzt entscheidest du dich, ob du die Nullhypothese verwirfst und deine Alternativhypothese annimmst (p < 0.05) – oder aber die Nullhypothese beibehältst (p > 0.05).

Geschafft!

Hut ab! Tapfer durchgehalten, wenn du bis hierher gelesen hast.

Ich hoffe, dass du jetzt für künftige Interpretationen des p-Werts gut gerüstet bist!

Probier's doch gleich mal aus: Lad' dir ein paar Datensätze runter und spiel damit!

Denn: Statistik darf tatsächlich Spaß machen!

auch wenn das erst mal kontraintuitiv erscheint...

QUELLEN (Als Amazon-Partnerin verdiene ich an qualifizierten Verkäufen):

Bortz, J., & Schuster, C. (2017). Statistik für Human- und Sozialwissenschaftler. Berlin: Springer.

Bühner, M., & Ziegler, M. (2017). Statistik für Psychologen und Sozialwissenschaftler. München: Pearson.

Field, A. (2018). Discovering Statistics using IBM SPSS Statistics. London: SAGE.

Sedlmeier, P., & Renkewitz, F. (2018). Forschungsmethoden und Statistik für Psychologen und Sozialwissenschaftler. München: Pearson.