In der Statistik hat man's ja zur allgemeinen Verwirrung ganz gern mit dem Wort "Standard" in allen erdenklichen Variationen: Standardabweichung, Standardnormalverteilung, Standardisierung, Standardschätzfehler – und last, but not least: Standardfehler!
Letzteren werde ich dir hier nahebringen.
Kurz & knackig:
Der Standardfehler des Mittels ist die Standardabweichung in einer THEORETISCHEN Verteilung von unendlich vielen Mittelwerten.
Was ist der Standardfehler?
Stell' dir vor, du machst eine Studie zur Resilienz bei Erwachsenen in Deutschland. Dazu fängst du 150 Erwachsene über 18 Jahren ein und zwingst sie zu einem Resilienztest.
Nun hast du 150 Resilienz-Werte, erhoben auf einer Skala von 0 (= gar nicht vorhanden) bis 100 (= der Fels / die Felsin in der Brandung). Aus diesen berechnest du (oder vermutlich eher SPSS) den Mittelwert.
Jetzt pinselst du liebevoll eine Skala und trägst den gefundenen Mittelwert auf der x-Achse ein.
Weil du so inspiriert und im Flow warst, machst du das Ganze gleich nochmal, an derselben Grundgesamtheit zur selben Fragestellung mit demselben Messinstrument für Resilienz.
Und nochmal. Und nochmal. Und nochmal. Das sieht dann irgendwann so aus:
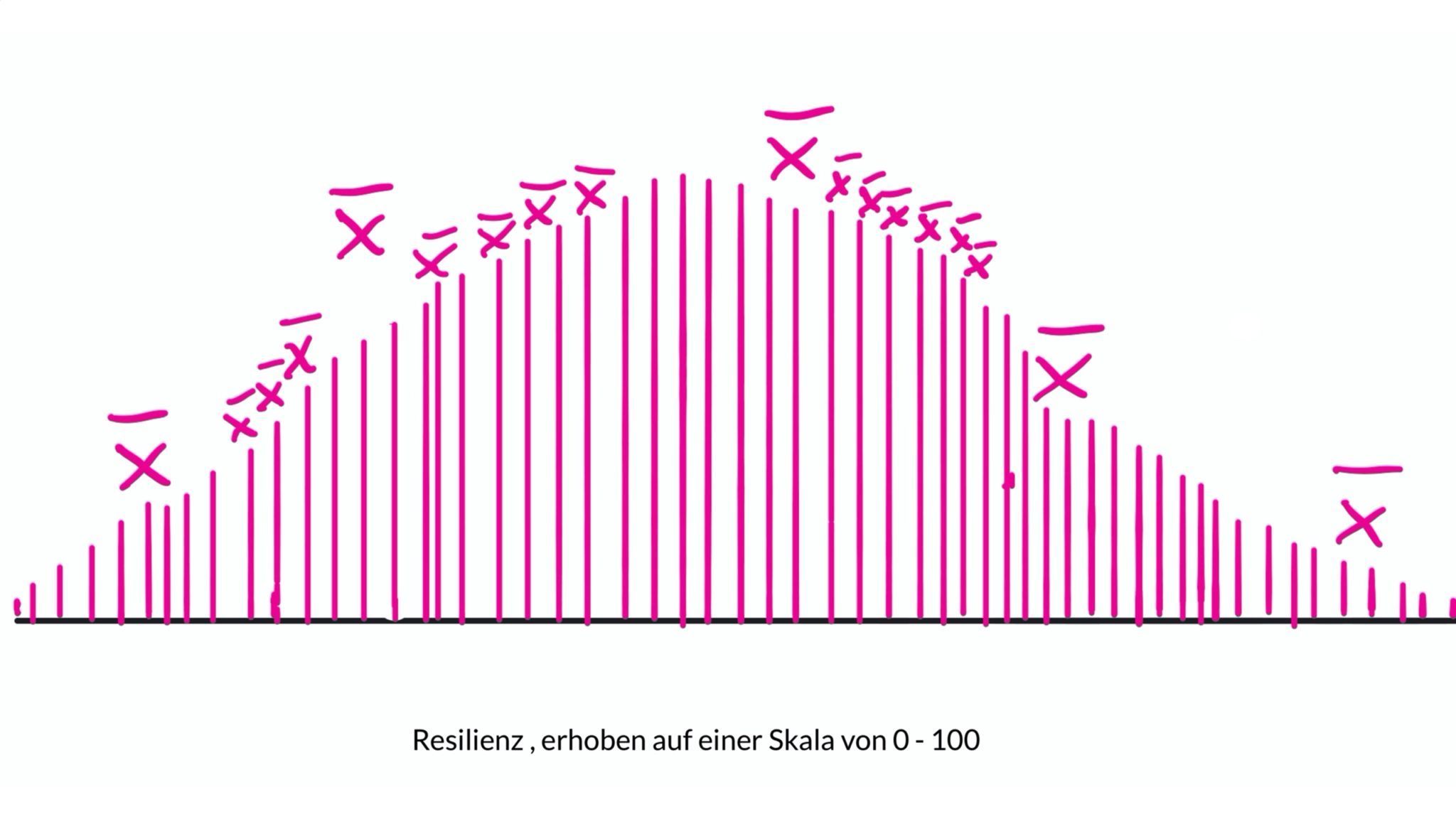
Vermutlich würdest du dir spätestens beim dritten Mal den Unmut der Befragten einhandeln, aber das hält dich nicht auf.
Du machst weiter ... ad infinitum und pinselst immer wieder die gefundenen Mittelwerte auf der x-Achse auf.
Dort, wo besonders viele Mittelwerte hinfallen, bildet sich ein "Huckel" und irgendwann entsteht aus all diesen Mittelwerten eine wunderschöne und sehr ansehnliche Normalverteilungskurve.
Wie du vermutlich schon gelernt hast, hat diese Normalverteilung ebenfalls wieder einen Mittelwert, also der Wert, der genau in der Mitte der Kurve, am höchsten Punkt, liegt.
Dieser Mittelwert aller Mittelwerte ist der Erwartungswert "mü", also der tatsächlich in der Population geltende Mittelwert, hier in grün eingezeichnet:
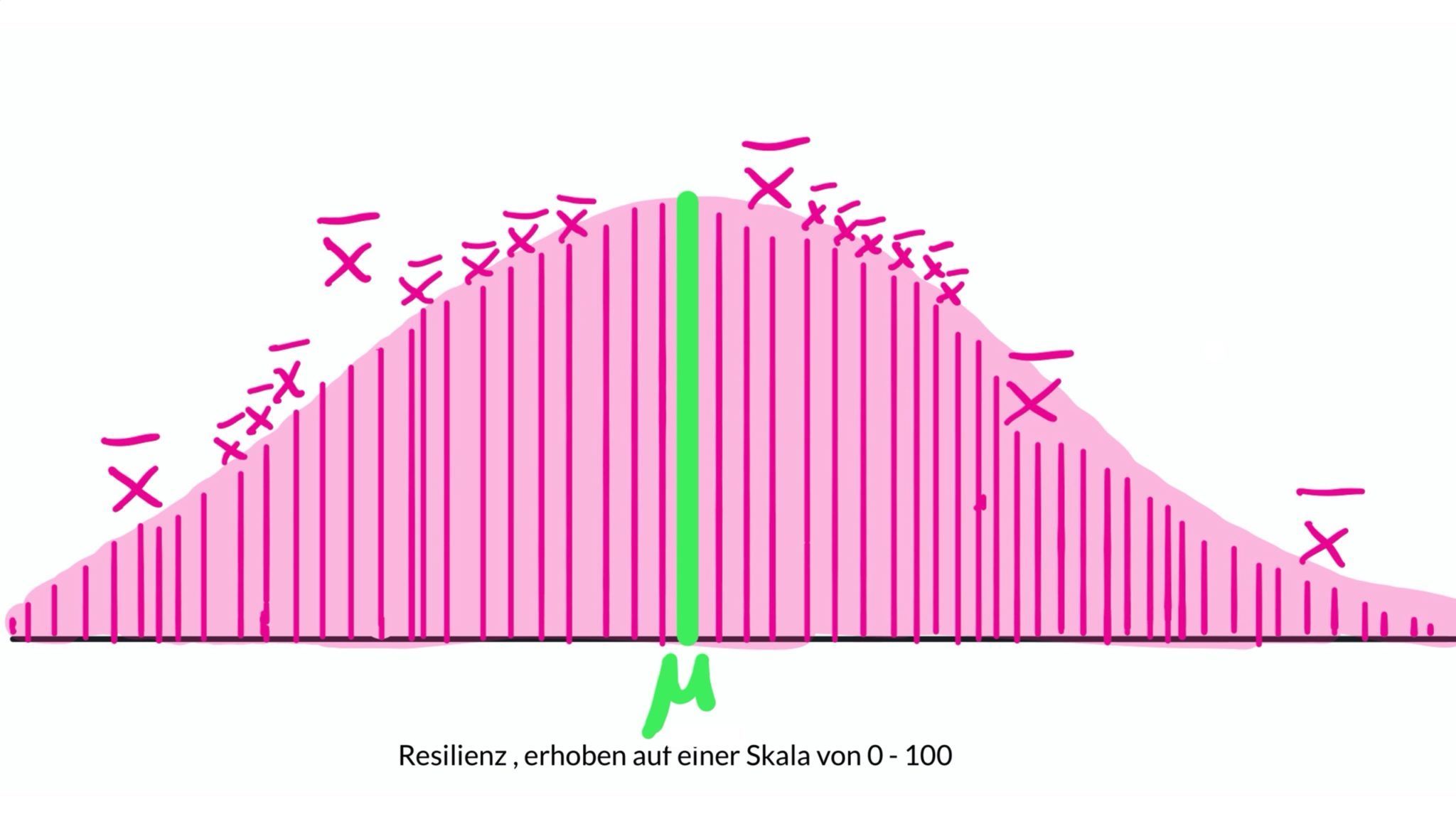
Und zu beiden Seiten um diesen Mittelwert herum gibt es auch eine Standardabweichung: das ist der Standardfehler.
Der Standardfehler ist daher die Standardabweichung in einer theoretischen Verteilung von Mittelwerten.
Denn wie du dir denken kannst, macht das natürlich niemand.
Das ist also eine rein theoretische Vorstellung. In der Praxis nimmt man nur eine repräsentative und zufällig ausgewählte Stichprobe und berechnet daraus den Standardfehler.
Und was sagt uns der Standardfehler bzw. wofür brauchen wir ihn?
Der Standardfehler des Mittels ist ein Maß dafür, wie gut der Mittelwert einer Stichprobe den Populationsmittelwert mü schätzt.
Je kleiner, desto besser trifft unser x quer den tatsächlich in der Grundgesamtheit geltenden Erwartungswert mü.
Hier siehst du den Standardfehler zu beiden Seiten des Mittelwerts / Erwartungswerts in gelb eingezeichnet:
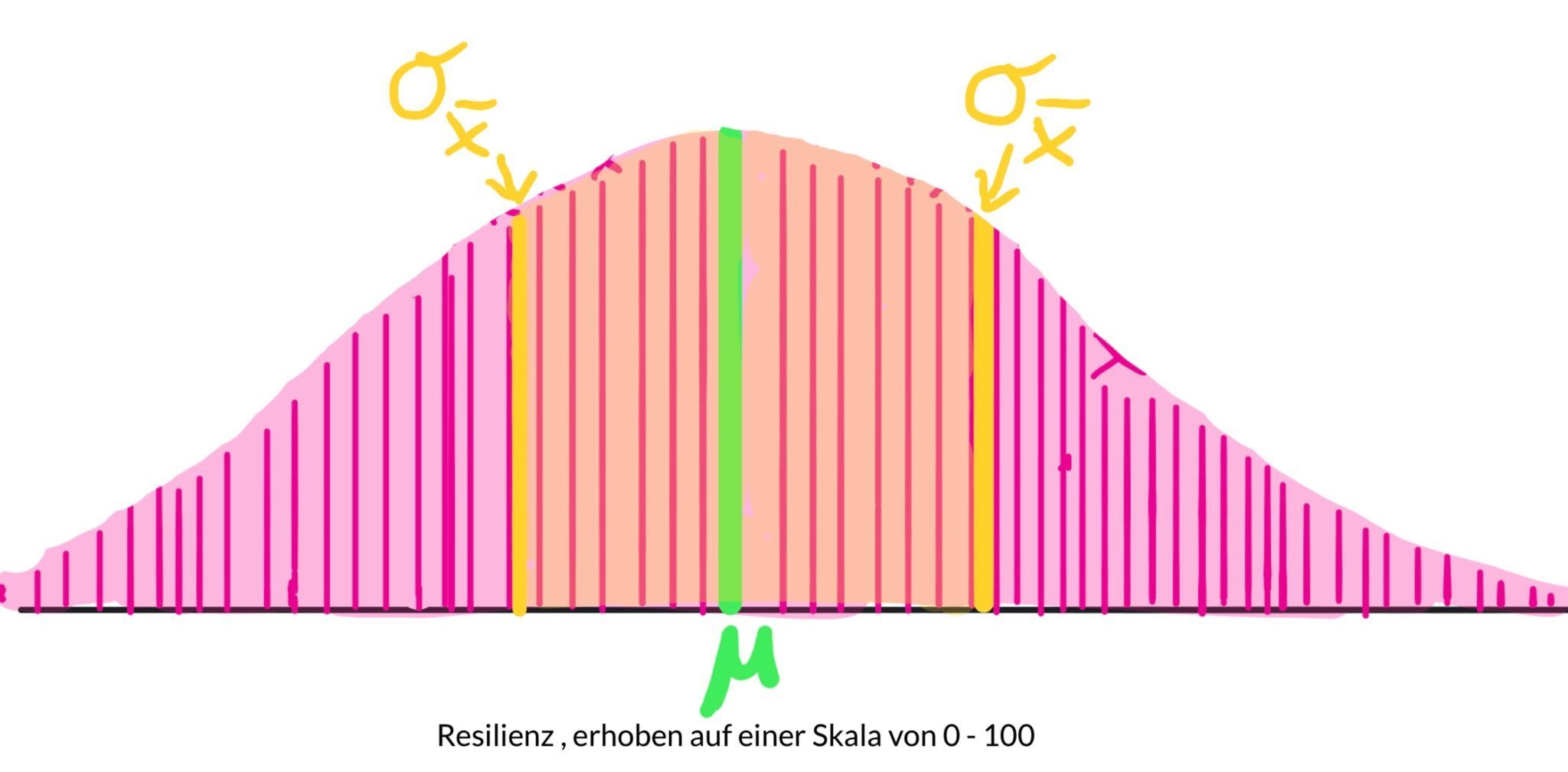
In welchen Bereich der Statistik gehört er?
Der Standardfehler gehört in die Welt der Inferenzstatistik und dort in den Bereich des theoretischen Grundwissens.
Dieses Wissen legt den Grundstein für das Verständnis der verschiedenen Verteilungen und darauf aufbauenden Methoden. Er ist nur bei metrischen Variablen anwendbar, d. h. ab Intervallskala.
Wie wird der Standardfehler berechnet?
Dies ist die Formel:
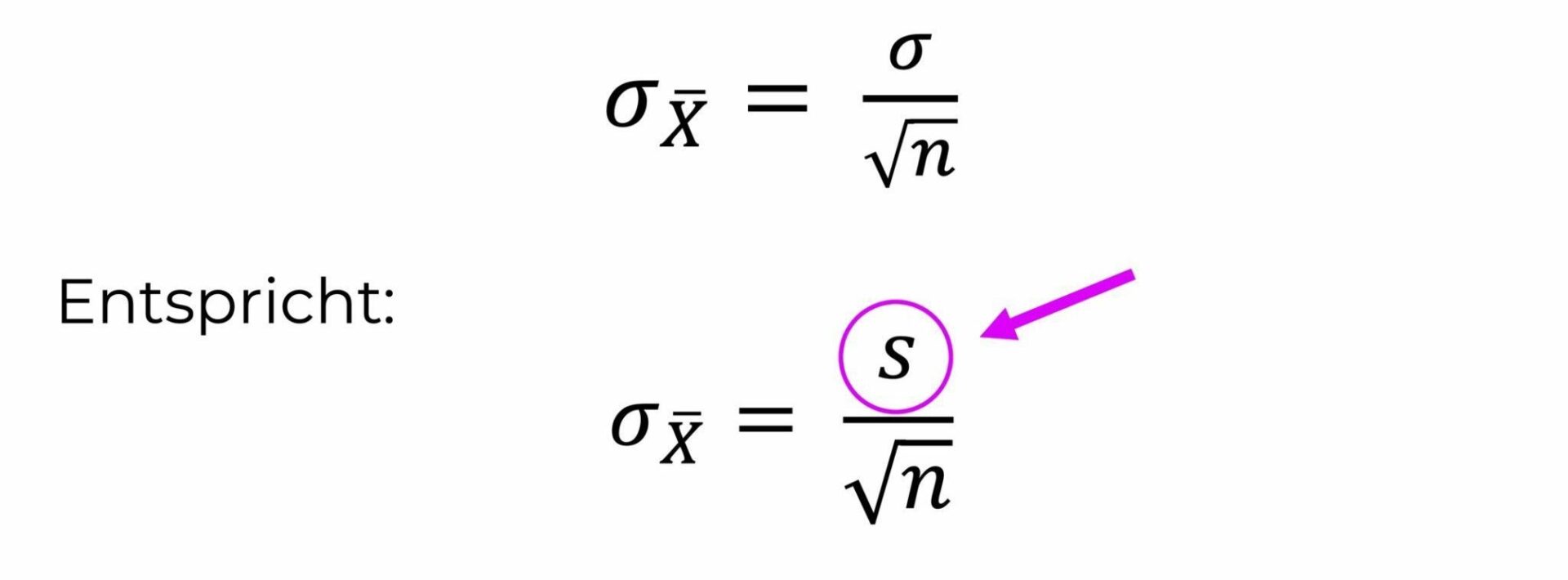
An der Formel kannst du sehen, dass der Standardfehler als Sigma (= Standardabweichung in der Population / Grundgesamtheit) mit einem tiefergestellten x quer definiert ist: als Standardabweichung in einer Verteilung von ganz vielen bunten Mittelwerten.
2 Schritte führen zum Standardfehler-Glück:
1. Standardabweichung aus deinen Stichproben-Daten berechnen
2. Durch Wurzel aus n teilen
Kommen wir zu unserem Resilienz-Beispiel zurück. Da ich dich hier nicht mit 150 Werten belasten will, beschränken wir uns auf eine Stichprobe von sagenhaften 8 Personen.
Resilienz-Werte: 56 80 66 74 59 65 48 70
Standardabweichung: 10.26 (wenn man durch n – 1 teilt!)
Mittelwert: 64.75
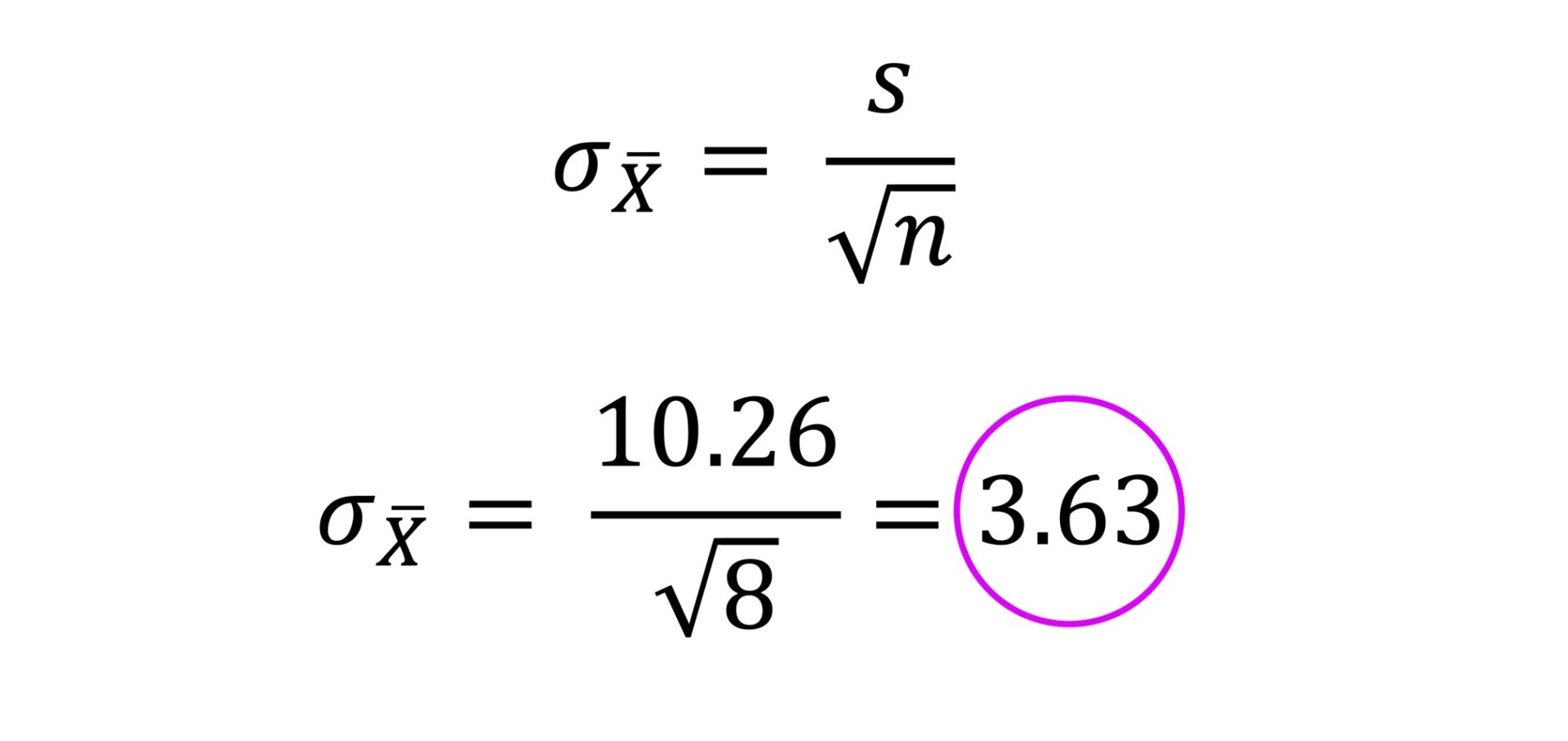
Beispiel größerer Datensatz:
Angenommen, wir würden die Untersuchung tatsächlich mit 150 Personen machen und würden auch dort eine Standardabweichung von 10.26 herausbekommen.
Dann sähe der Standardfehler des Mittels folgendermaßen aus:
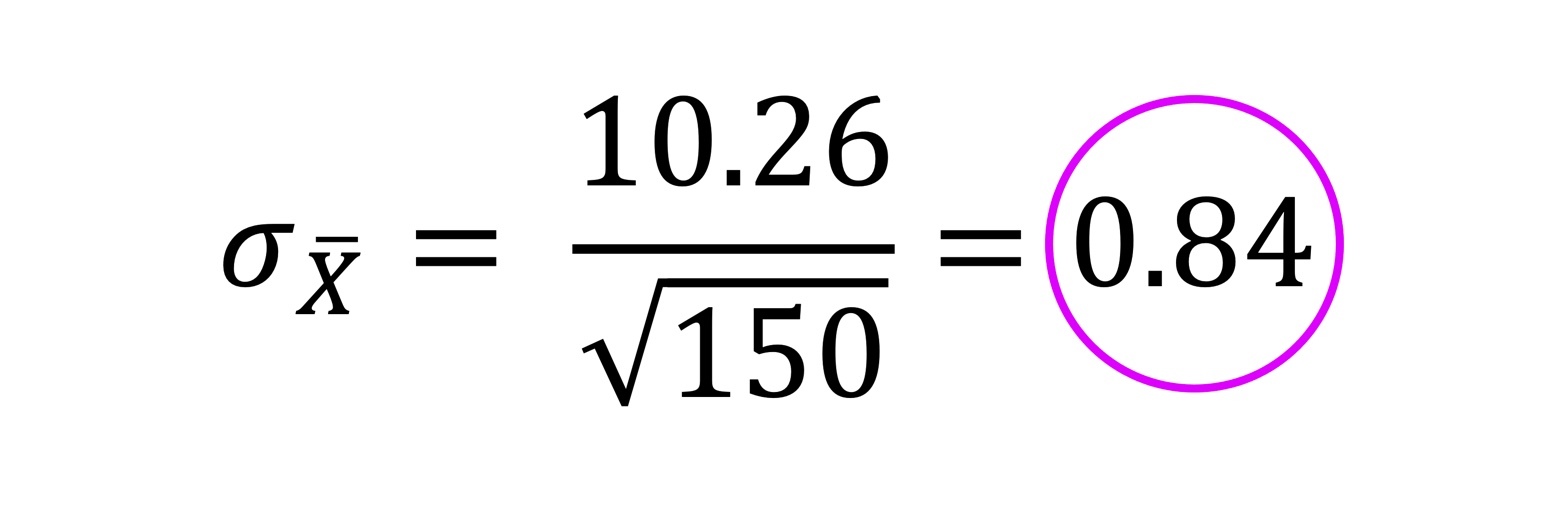
Du siehst also, dass er deutlich kleiner geworden ist. Daher gilt:
Je größer die Stichprobe, desto kleiner der Standardfehler und desto genauer die Schätzung des Populationsmittelwerts!
Wie wird der Standardfehler interpretiert?
Hier gibt es leider keine klaren Regeln oder Konventionen!
Wichtig ist wie bei den meisten anderen statistischen Interpretationen auch, dass du die verwendete Skala im Hinterkopf behältst. Denn je nachdem wie groß die Skala ist, wirst du zu einer unterschiedlichen Interpretation kommen.
Idealerweise liegt der Standardfehler des Mittels jedoch unter 1.
Mehr zum Standardfehler und generell zur Inferenzstatistik findest du in meinem ganz wunderbaren
Buch "Schließende Statistik einfach erklärt! Von Null auf Statistik-Profi mit Schritt-für-Schritt-Anleitungen",
das du HIER bekommst.
Wie sag ich's Tante Erna?
Stell dir vor, du bist bei deiner Tante Erna zu Schwarzwälder Kirschtorte und ordentlich Kaffee eingeladen.
Tante Erna ist nicht die allerfirmste in Statistik, aber stets super interessiert an allem, was du so erhebst.
Also musst du ihr deine Ergebnisse in lai*innen-verständlicher Form nahebringen.
Das sähe hier so aus:
"Die Versuchspersonen waren insgesamt überdurchschnittlich psychisch widerstandsfähig." = Mittelwert von 64.75 auf einer Skala von 0 – 100
"Man kann davon ausgehen, dass das Ergebnis ziemlich gut das Gros aller Erwachsenen in Deutschland widerspiegelt." = Standardfehler von 0.84
Zum Abschluss noch ein Steckbrief:
Steckbrief Standardfehler des Mittels
Meine Challenge an dich
Schnapp dir gleich mal einen Datensatz, den du entweder bereits hast oder erfinde einen.
Und dann rechne bitte den Standardfehler aus und versuch dich an einer Interpretation für Tante Erna.
Viel Spaß!
Quellen:
Bortz, J., & Schuster, C. (2017). Statistik für Human- und Sozialwissenschaftler. Springer.
Field, A. (2018). Discovering Statistics using IBM SPSS Statistics. SAGE.
Sedlmeier, P., & Renkewitz, F. (2018). Forschungsmethoden und Statistik für Psychologen und Sozialwissenschaftler. Pearson.
