Seinerzeit, als noch schummriges Kerzenlicht statt Neonröhren das Arbeitszimmer der Statistiker*innen erhellte, führte man geduldig die komplexesten Berechnungen per Hand durch – nur um dann möglicherweise von einem Kollegen auf einen minimalen Fehler in Zeile 68 hingewiesen zu werden...
Diese düsteren Zeiten sind dankenswerterweise vorbei, denn heute genügen ein paar Klicks an der richtigen Stelle, und schon spuckt SPSS (oder jedes andere Statistik-Programm) bereitwillig gefühlte 50.000 Zahlen in umfangreichen Tabellen aus.
Doch das Problem, das sich uns trotz blitzschneller Computer-Berechnungen in der heutigen Zeit (nicht nur bei SPSS...) stellt, ist: Wie sollen wir aus dem Overload an Informationen das Wesentliche herauslesen? Wohin sollen wir unser Augenmerk richten? Welche der vielen bunten Zahlen sind relevant? Wie erkenne ich, ob ein Ergebnis signifikant ist?
Um etwas Licht ins undurchdringliche Dickicht der Zahlen zu bringen, zeige ich dir in diesem und den nachfolgenden Teilen zum Thema SPSS Outputs, wo du was ablesen und – nicht ganz unwesentlich – wie du das Ganze interpretieren kannst!
Dabei beginnen wir diesmal mit den Häufigkeiten und der "Explorativen Datenanalyse", gefolgt von der Analyse des Zusammenhangs zwischen nominalskalierten Daten. In den nächsten Teilen folgen dann weitere Methoden.
Damit du alles selbst nachvollziehen kannst, schreibe ich dir die jeweiligen Schritte dazu, um die abgebildeten Ergebnistabellen zu erhalten.
Dabei gehe ich davon aus, dass du statistisches Vorwissen hast und dich mit der grundsätzlichen Bedienung von SPSS auskennst. Natürlich kannst du dir alles auch nur so durchlesen, ohne die Daten selbst aufzurufen.
Hast du was anderes gesucht? Klick' hier für SPSS für Zusammenhangsmaße, hier für t-Test und Regression sowie hier für die Varianzanalyse.
Wo du Datensätze zum Üben herbekommst
Datensätze bekommst du auf verschiedensten Seiten im Internet sowie direkt im Programm SPSS. Ich empfehle z. B. die Datensätze von Andy Field, die hier zu finden sind.
Praktischerweise liefert SPSS aber auch eine Fülle von Datensätzen mit, die du folgendermaßen erreichen kannst:
Windows: C:/Programme/IBM/SPSS/Statistics/29 (oder eine andere Version)/Samples/German
Mac: Im Finder: Applications oder Programme/IBM/SPSS/Statistics/29 (oder eine andere Version)/Samples/German
HÄUFIGKEITEN
Die nachfolgenden Outputs entstammen alle dem Datensatz survey_sample.sav im SPSS-Samples-Folder, der knackige 46 Variablen und 2.832 Fälle aus den USA enthält. Bitte suche und öffne ihn – und los geht's mit den Häufigkeiten:
Gehe auf "Analysieren", "Deskriptive Statistiken", "Häufigkeiten". Im sich öffnenden Fenster wählst du die Variablen Familienstand (Nominalskala), Anzahl an Kindern (Absolutskala)und höchster Abschluss (Ordinalskala) aus und drückst auf "OK". Du erhältst die untenstehende Ergebnistabelle.
Was du hier ablesen kannst, ist Folgendes:

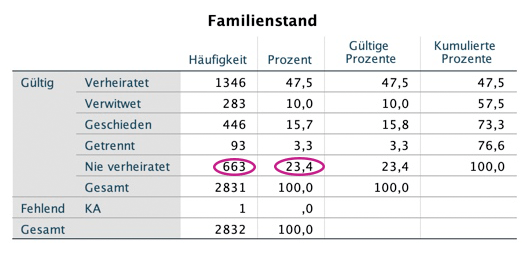

für hinter die löffelchen:
SPSS rechnet ALLES für dich – auch wenn es inhaltlich keinen Sinn ergibt!
Daher ist Mitdenken angesagt.
In der obigen Tabelle ist es z. B. wenig sinnvoll, die kumulierten Prozente beim Familienstand zu interpretieren (das wäre eine Fragestellung wie "Welcher Prozentsatz ist höchstens verwitwet?") – denn das würde implizieren, dass eine Rangordnung besteht im Sinne von: Geschieden ist höher/besser als verwitwet ...
EXPLORATIVE DATENANALYSE
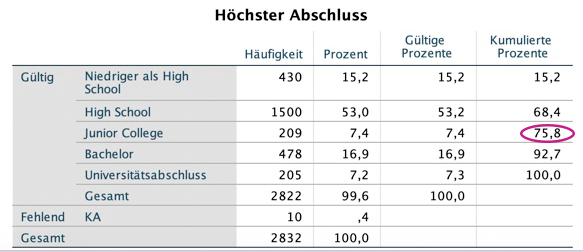
Der nächste Menüpunkt bei "Analysieren", "Deskriptive Statistiken" ist die "Deskriptive Statistik". Da diese Auswertungen jedoch auch in der deutlich umfassenderen Auswertung der "Explorativen Datenanalyse" enthalten sind, begeben wir uns gleich zu letzterer.
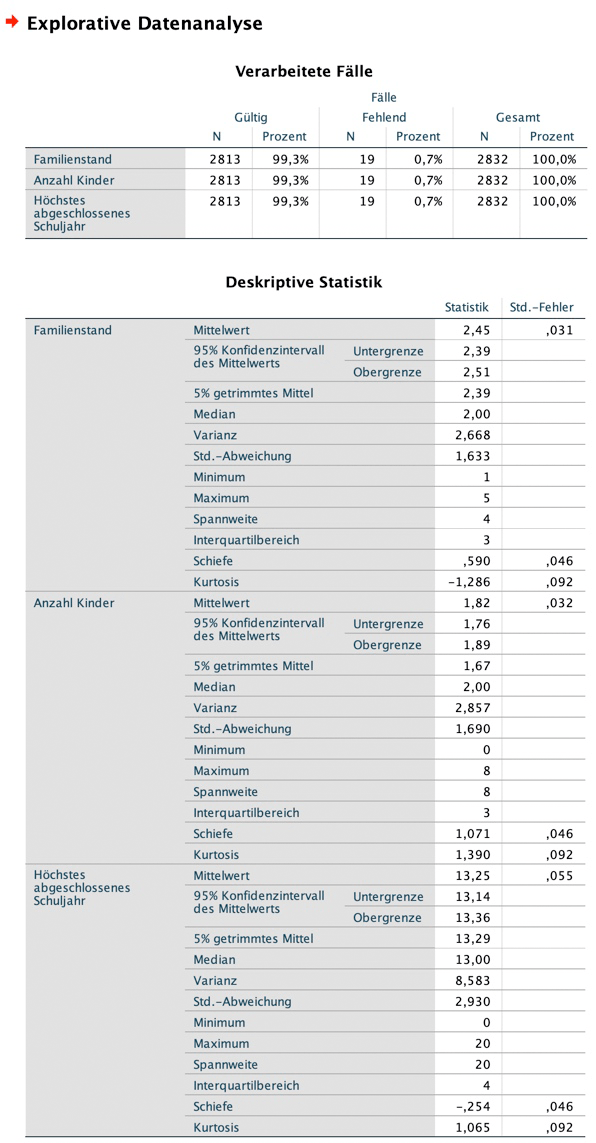
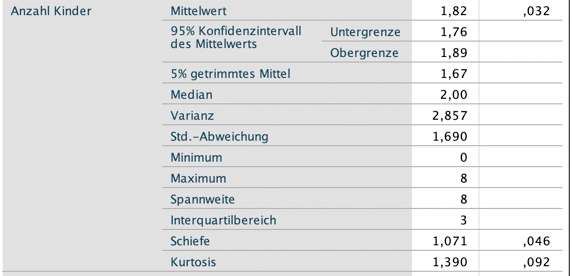
Geh auf "Analysieren", "Deskriptive Statistiken", "Explorative Datenanalyse". Im sich öffnenden Fenster wählst du wieder die Variablen Familienstand (Nominalskala), Anzahl an Kindern (Absolutskala) und höchster Abschluss (Ordinalskala) aus, verschiebst sie in das Feld "Abhängige Variablen" und drückst auf "OK".
Was du hier ablesen kannst, ist Folgendes:

Brauchst du Hilfe beim lernen von statistik?
Dann komm zu Statistik-gym,
dem Online-Fitnessstudio für Statistik,
das dich fit für die Prüfung macht!
Eine Mitgliedschaft wie im Fitness-Studio oder bei Streaming-Anbietern, nur eben für Statistik im Bachelor,
die dir hilft, dieses Fach endlich zu verstehen & die Prüfung zu meistern!
Darin bekommst du:
Und dann macht Statistik vielleicht sogar Spaß!
Klingt gut? Dann klick hier:
Variable "Anzahl Kinder"

KREUZTABELLEN, CHI-QUADRAT,
KONTINGENZKOEFFIZIENT, PHI & CRAMÉRS V
Geh auf "Analysieren", "Deskriptive Statistiken", "Kreuztabellen". Im sich öffnenden Fenster klickst du die beiden nominalskalierten Variablen Familienstand (Zeilen) sowie "Glaube an Leben nach dem Tod" (Spalten) an. Es macht für das Ergebnis übrigens keinerlei Unterschied, welches Merkmal du den Zeilen oder Spalten zuordnest.
Jetzt klickst du auf das Kästchen "Statistiken" auf der rechten Seite und setzt bei "Chi-Quadrat", "Kontingenzkoeffizient", "Phi und Cramer-V" einen Haken, drückst auf "weiter" und dann auf "OK". Du erhältst den nachfolgenden Output.
Was du hier ablesen kannst, ist Folgendes:
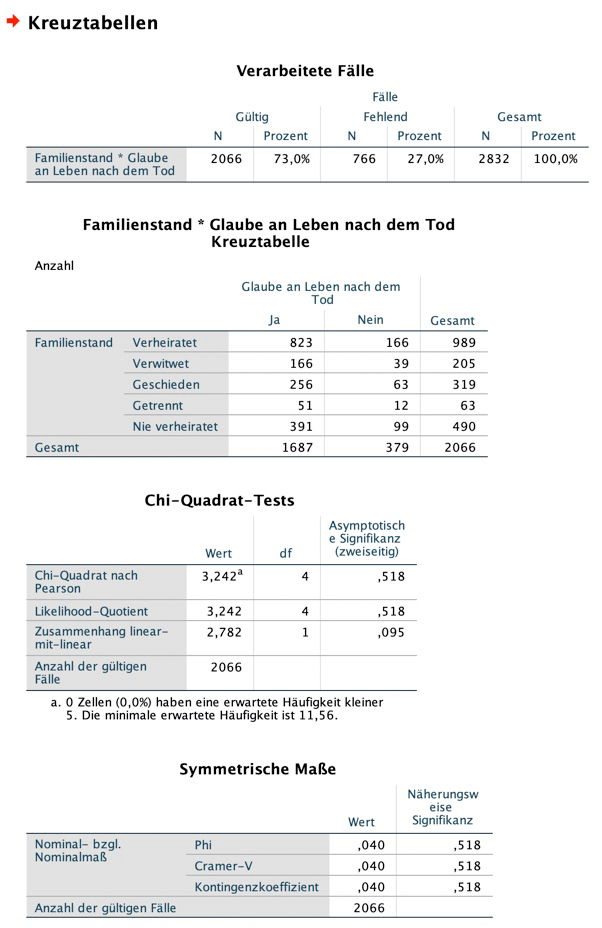
Chi-Quadrat-Test

Phi, Cramérs V & Kontingenzkoeffizient

Geschafft!
Ich hoffe, es fällt dir nun etwas leichter, dich in den Ergebnistabellen zurechtzufinden!
Vielleicht hast du ja sogar Lust, dir gleich einen weiteren Datensatz zu schnappen und das Ganze anzuwenden.
Jetzt ist aber erst mal Zeit für einen wohlverdienten Schokokuchen!

QUELLEN (Als Amazon-Partnerin verdiene ich an qualifizierten Verkäufen):
Bühner, M., & Ziegler, M. (2017). Statistik für Psychologen und Sozialwissenschaftler. Pearson.
Bortz, J., & Schuster, C. (2017). Statistik für Human- und Sozialwissenschaftler. Springer.
Field, A. (2018). Discovering Statistics using IBM SPSS Statistics. SAGE.
QUELLEN (Als Amazon-Partnerin verdiene ich an qualifizierten Verkäufen):
Bortz, J., & Schuster, C. (2017). Statistik für Human- und Sozialwissenschaftler. Berlin: Springer.
Field, A. (2018). Discovering Statistics using IBM SPSS Statistics. London: SAGE.


Vielen Dank für den tollen Text!
Dankeschön, lieber Klaus!
Klasse! Das bringt Licht ins Dunkel.
Freut mich sehr, Peter!
Liebe Grüße
Spitze erklärt! Vielen Dank!!
Freut mich, liebe Sarah, und sehr gerne!
Liebe Grüße,
Melanie