Chi-Quadrat-Test auf Unabhängigkeit einfach erklärt!
Vermutlich wolltest du immer schon mal wissen, ob es einen Zusammenhang zwischen dem Geschlecht und der Wahl der Dating-App gibt. Nein? Vielleicht etwas Ähnliches? Wenn ja, hat das Warten nun ein Ende, denn wenn du tapfer weiterliest, werde ich dich in die Geheimnisse des Chi-Quadrat-Tests auf Unabhängigkeit einweihen – derjenigen Methode, mit der du herausfinden kannst, ob zwischen zwei nominalskalierten Merkmalen ein Zusammenhang besteht.
Was ist der Chi-Quadrat-Test auf Unabhängigkeit?
Chi-Quadrat klingt ja irgendwie ein wenig fernöstlich (= potenzierte Lebensenergie?), hat damit allerdings eher wenig zu tun. Dafür umso mehr mit einem statistischen Verfahren, bei dem überprüft wird, ob zwei nominalskalierte, kategoriale Variablen wie z. B. Geschlecht, Nationalität, Studienfach, Wahl der Automarke, gewählte Partei etc. zusammenhängen.
Der Begriff "Unabhängigkeit" bedeutet, dass kein Zusammenhang zwischen den Variablen besteht!
Das ist auch die Nullhypothese, die dieser Test überprüft, beispielsweise: "Es besteht kein Zusammenhang zwischen einer bestimmten Persönlichkeitsstörung und dem gewählten Studienfach".
Anders formuliert: Die Wahl des Studienfaches ist unabhängig von einer eventuell vorhandenen Persönlichkeitsstörung. Oder so: Die vorliegende Persönlichkeitsstörung hat keinen Einfluss auf die Wahl des Studienfaches (und umgekehrt).
Möglich ist auch, den Test mit Variablen durchzuführen, die auf einer höheren Skala liegen. In diesem Fall müsste man die Variablen dann quasi "downgraden" und in Kategorien verpacken (was jedoch immer mit Informationsverlust verbunden ist).
In welchen Bereich der Statistik gehört er?
Der Chi-Quadrat-Test gehört in die Welt der Inferenzstatistik, dient also dazu, von den Daten einer Stichprobe auf die dazugehörige Grundgesamtheit zu schließen. Der Test basiert auf dem Chi-Quadrat-Koeffizienten, den du bereits aus der deskriptiven Statistik kennen müsstest.
Zudem gehört er in den Bereich der Zusammenhangshypothesen.
Was sagt der Chi-Quadrat-Test aus?
Der Chi-Quadrat-Test sagt aus, ob ein Zusammenhang zwischen zwei nominalskalierten Variablen besteht und wenn ja, wie stark dieser ist. Die Berechnung der dazugehörigen Effektgröße wird hier jedoch nicht dargestellt.
Als grobe Daumenregel gilt zunächst einmal: kleiner Wert = geringer Zusammenhang; großer Wert = starker Zusammenhang.
Hier gibt es leider keine Normierung, daher kann der Chi-Quadrat-Wert, der bei deiner Berechnung herauskommt, potenziell beliebig groß werden – er ist jedoch immer positiv. Das macht die Interpretation ein wenig schwierig...
Man kann jedoch einen Maximalwert berechnen und erhält dadurch einen gewissen Anhaltspunkt. Das zeige ich dir nachher bei der Berechnung.
Zudem kannst du bei einem signifikanten Ergebnis die Effektstärke Klein Omega oder Cramérs Phi berechnen.
Chi-Quadrat-Test berechnen
Kommen wir für die Berechnung zum Eingangsbeispiel zurück:
Gibt es einen Zusammenhang zwischen dem Geschlecht und der Wahl einer Dating-App?
Um das Beispiel möglichst einfach zu halten, definieren wir die Ausprägungen von Geschlecht ganz old school als weiblich und männlich. Die Dating-Apps oder Single-Börsen sind Parship und Tinder (selbstverständlich ist der Chi-Quadrat-Unabhägigkeitstest auch mit mehr als nur zwei Ausprägungen pro Merkmal anwendbar!).
Dazu wurden jeweils 20 Frauen und Männer befragt.
Hier ist dazu die sogenannte Kreuz- oder Kontingenztabelle:
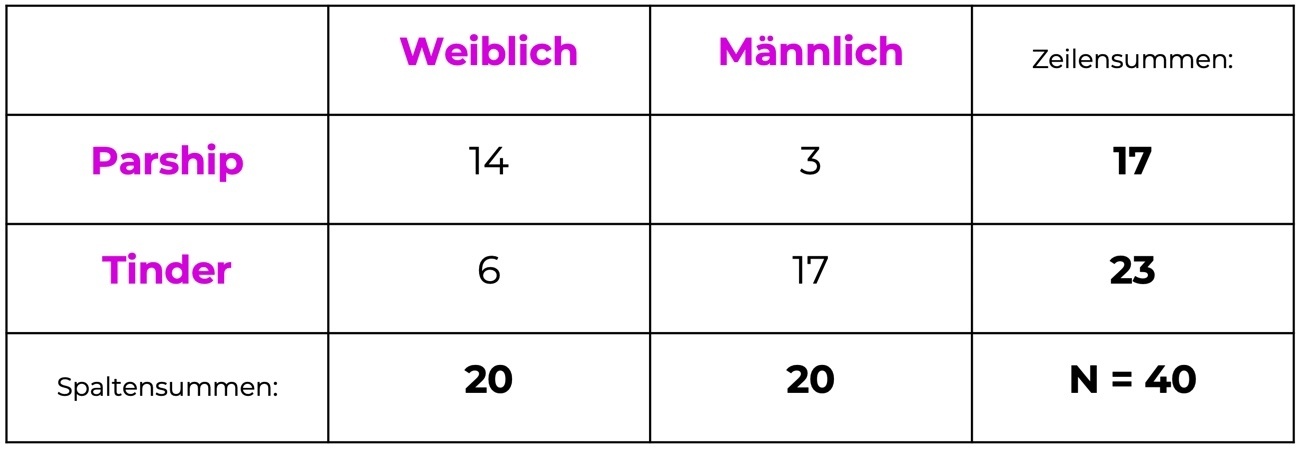
Grundprinzip der Berechnung
Um die Frage nach dem Zusammenhang zu überprüfen, wird berechnet, wie häufig eine bestimmte Merkmalskombination (also z. B. Frau und Parship) vorliegen müsste, wenn kein Zusammenhang bestünde – das ist die erwartete Häufigkeit.
Diese erwartete Häufigkeit wird dann mit den tatsächlich vorhandenen Häufigkeiten in der Kreuztabelle verglichen.
GIBT ES (SIGNIFIKANTE) ABWEICHUNGEN ZWISCHEN DEN THEORETISCH ERWARTETEN UND DEN TATSÄCHLICH BEOBACHTETEN HÄUFIGKEITEN, LIEGT EIN ZUSAMMENHANG VOR!
Dies ist die Formel für die Berechnung des Chi-Quadrat-Koeffizienten (das x-Quadrat ist die mathematische Notation für Chi-Quadrat!):
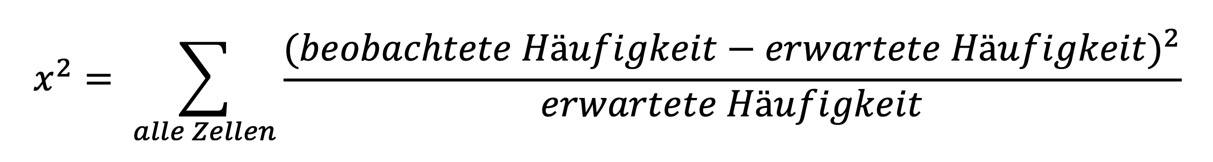
Die beobachtete Häufigkeit ist das, was du in der Kreuztabelle siehst.
Wie bekommst du nun die erwartete Häufigkeit?
Dazu multiplizierst du für jede Zelle jeweils die zu dieser Merkmalskombination dazugehörige Zeilensumme mit der dazugehörigen Spaltensumme und teilst das Ergebnis dann durch das Gesamt-N:

Um herauszufinden, wieviele Frauen Parship nutzen würden, wenn es keinen Zusammenhang zwischen dem Geschlecht und der Wahl der Dating-App gäbe, rechnest du:
Weiblich / Parship: (Zeilensumme 17 x Spaltensumme 20) : 40 = 8,5
Hier sehen wir bereits, dass mehr Frauen als erwartet Parship wählen, nämlich 14.
Prüfen wir jetzt noch die anderen Zellen:
Weiblich / Tinder: (23 x 20) : 40 = 11.5 – beobachtet wurden jedoch 6, also weniger
Männlich / Parship: (17 x 20) : 40 = 8.5 – beobachtet wurden jedoch 3, also deutlich weniger!
Männlich / Tinder: (23 x 20) : 40 = 11.5 – beobachtet wurden jedoch 17, also deutlich mehr!
Nächster Schritt:
Alles in die Formel einsetzen und sich den Wolf rechnen – das Ergebnis ist dann der Chi-Quadrat-Koeffizient:
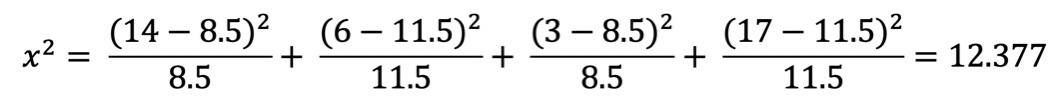
Und was sagt uns das jetzt?
Noch nicht so viel... Immerhin können wir ausrechnen, wie groß der Chi-Quadrat-Wert /-Koeffizent in unserem Beispiel maximal werden könnte:
Wertebereich Chi-Quadrat-Koeffizient
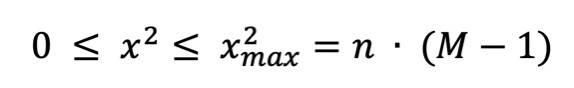
Hier kannst du sehen, dass der Chi-Quadrat-Wert nicht negativ wird.
Der maximal mögliche Wert wird berechnet, indem du die Stichprobengröße mit (M - 1) multiplizierst. Dabei ist M der kleinere Wert der Anzahl von Zeilen und Spalten. Dazu ein Beispiel:
Angenommen, wir hätten bei Geschlecht noch "divers" hinzugenommen, dann hätten wir drei Spalten für das Geschlecht und zwei für die Dating-Apps gehabt. In diesem Fall wäre dann der kleinere Wert der Anzahl von Zeilen und Spalten die zwei, da es zwei Dating-Apps und drei Geschlechts-Ausprägungen geben würde.
Da wir in unserem Beispiel jeweils zwei Ausprägungen haben, ist es also einfach die zwei.
Somit wäre der maximal mögliche Wert hier:
40 x (2 - 1) = 40 (da sind wir mit unserem gefundenen Wert von 12.377 noch etwas davon entfernt).
Um das Ganze jetzt statistisch auf Signifikanz zu überprüfen, brauchen wir SPSS (oder eine Chi-Quadrat-Tabelle):
Chi-Quadrat-Test mit SPSS
Zur Erinnerung – die getestete Nullhypothese lautet: Es liegt KEIN Zusammenhang zwischen den Variablen vor!
Wenn du nun ein signifikantes Ergebnis erhältst (einen p-Wert kleiner 0,05), wird die Nullhypothese verworfen und die Alternativhypothese angenommen, die da lautet:
Es liegt ein signifikanter Zusammenhang zwischen den beiden Variablen vor.
Zur Vorgehensweise:
Ruf' zunächst deinen Datensatz auf (oder gib' selbst Daten ein).
Dann gehst du auf "Analysieren", "Deskriptive Statistiken", "Kreuztabellen". Im sich öffnenden Fenster klickst du die beiden nominalskalierten Variablen an, die dich interessieren, und ordnest sie den Zeilen oder Spalten zu. Es macht für das Ergebnis übrigens keinerlei Unterschied, welches Merkmal du den Zeilen oder Spalten zuordnest.
Jetzt klickst du auf das Kästchen "Statistiken" auf der rechten Seite und setzt bei "Chi-Quadrat" einen Haken, drückst auf "weiter" und dann auf "OK". Es erscheint der nachfolgende Output.
Ein weiteres Beispiel dazu findest du hier.

Fazit für unsere Untersuchung:
Je mehr Mann, desto mehr Tinder – und je mehr Frau, desto mehr Parship... (caveat: Das ist eine sehr flapsige und keineswegs statistisch korrekte Interpretation!).
Oder so: Es gibt einen signifikanten Zusammenhang zwischen dem Geschlecht und der Wahl der Dating-App: Männer neigen eher zu Tinder, wohingegen Frauen Parship präferieren.
Zu guter Letzt noch ein kleiner Steckbrief:
Steckbrief Chi-Quadrat-Test
Quellen (Als Amazon-Partnerin verdiene ich an qualifizierten Verkäufen):
Bortz, J., & Schuster, C. (2017). Statistik für Human- und Sozialwissenschaftler. Berlin: Springer.
Field, A. (2018). Discovering Statistics using IBM SPSS Statistics. London: SAGE.
Geschafft – Geht doch!
Wenn ich dir einen kleinen Vorschlag machen dürfte, würde ich sagen, du schnappst dir einen Datensatz (z. B. von Andy Field) oder erfindest selbst einen mit einer überschaubaren Anzahl von Werten, überlegst dir eine sinnvolle Fragestellung und übst gleich einmal die Anwendung – entweder per Hand und/oder mit SPSS.
Viel Erfolg!
Und natürlich nicht vergessen: Belohnen!
Statistik kann ja gerne mal ein wenig dröge sein.
Daher sollte man sich's danach oder währenddessen unbedingt gut gehen lassen:

Foto von Maddi Bazzocco auf Unsplash

Kann man nur durch ablesen der Kreuztabelle feststellen, in welche Richtung der signifikante Zusammenhang geht oder gibt es noch eine „elegantere“ Lösung? Wenn nicht, wie berichtet man dann in der Arbeit darüber korrekt?
Hallo Dannik,
ja, das geht meines Erachtens nur über das Herauslesen aus der Tabelle.
Hier findest du, wie du das korrekt berichtest (ganz unten):
https://statistikguru.de/spss/chi-quadrat-test-unabhaengigkeit/interpretation.html
Wobei ich anschließend auf jeden Fall noch berichten würde, in welche Richtung der Zusammenhang geht.
Liebe Grüße,
Melanie