Mythos und Realität des p-Werts…p-Wert einfach erklärt!
Mythen und Märchen unterschiedlichster Couleur ranken sich um den p-Wert. Manche sagen, das habe irgendwie was mit Wahrscheinlichkeit zu tun, andere behaupten, das sei das, was in der Spalte "Sig." bei SPSS stünde, und wiederum andere meinen, der p-Wert sei die Wahrscheinlichkeit für die Nullhypothese (oder war's die Alternativhypothese?).
Um ein wenig Licht ins sagenumwobene Dunkel zu bringen, folgt hier zunächst die Kurzversion und anschließend eine ausführlichere Erklärung.
Die Kurzversion – quick & dirty
Der p-Wert zeigt an, wie wahrscheinlich dein Ergebnis ist, WENN DIE NULLHYPOTHESE STIMMEN WÜRDE.
Oder so: Der p-Wert ist eine BEDINGTE WAHRSCHEINLICHKEIT – nämlich die Wahrscheinlichkeit für dein spezielles Ergebnis (Mittelwert, Korrelation, F-Test etc.), unter der bedingung, dass die NULLHYPOTHESE Gilt.
Vielleicht auch so: Wenn die Nullhypothese stimmen würde – wie wahrscheinlich ist dann dein Ergebnis?
Für die weitere Auswertung gilt gemäß der meist (noch) geltenden Konvention:
Ist der p-Wert, den man bei SPSS unter "Sig." ablesen kann, kleiner als .05 (p < 0.05) – ist dein Ergebnis also so unwahrscheinlich, dass es kein Zufall mehr sein kann – , so liegt ein signifikantes Ergebnis vor und die Nullhypothese wird verworfen.
CAVEAT: Ich setze in diesem Artikel Wissen zum Hypothesentesten und zu Verteilungen voraus! Falls du damit noch nicht vertraut bist, hast du wahrscheinlich mehr davon, wenn du dich erst mal ein wenig dazu schlau machst.
Grundsätzliches, um dich thematisch einzunorden
Die Basis des p-Werts: Verteilungen
Wenn du Hypothesentests durchführst, tust du das immer vor dem Hintergrund einer bestimmten Verteilung.
Das kann z. B. die Normal- bzw. Standardnormalverteilung sein, oder aber die F-, Chi-Quadrat- oder t-Verteilung – jeweils abhängig vom Inhalt deiner Hypothese. Eine Verteilung enthält 100% aller Werte – oder in Wahrscheinlichkeiten ausgedrückt: die Fläche unter der Kurve ist stets 1.
Du testest immer ein Modell: eine Vorstellung davon, wie die Daten unter Gültigkeit der Nullhypothese verteilt sind. Wobei die Nullhypothese besagt, dass der postulierte Unterschied oder Zusammenhang NICHT existiert. Beim Hypothesentesten geht es also darum, zu überprüfen, ob die Nullhypothese nach wie vor gilt – oder aber verworfen wird.
Als Ergebnis deines Hypothesentests erhältst du einen Wert (z. B. einen t-, z- oder F-Wert), der in der dazugehörigen Verteilung liegt.
Die Wahrscheinlichkeit dafür, dass dein Ergebnis-Wert genau an diesen bestimmten Punkt in der jeweiligen Verteilung fällt (wenn die Nullhypothese gilt), ist der p-Wert.
Beispiel t-Test:
Du führst eine Untersuchung zur Frage durch, ob Männer geduldiger sind als Frauen. Dann wäre die Nullhypothese: "Frauen und Männer unterscheiden sich nicht in ihrer Geduld.", wohingegen deine Alternativhypothese lautet: "Männer sind geduldiger als Frauen." (rechtsseitiger Test).
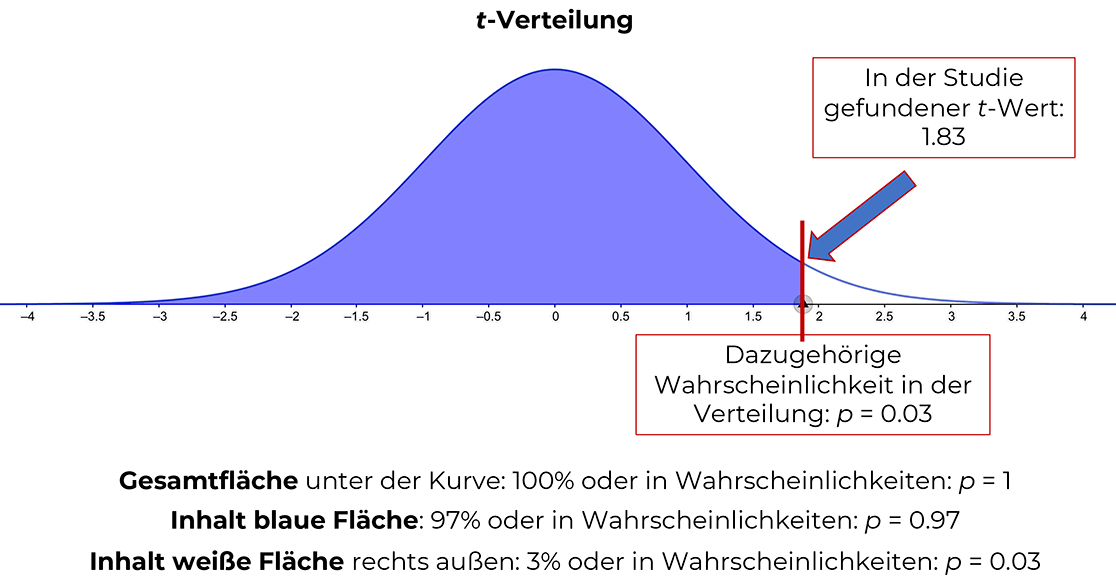
Da die Varianz unbekannt ist und es um Mittelwerts-Unterschiede geht, führst du einen t-Test durch und lässt 5% Irrtumswahrscheinlichkeit zu (α = 0.05). Nun erhältst du bei deiner Auswertung zum Beispiel einen t-Wert von 1.83.
Dessen Wahrscheinlichkeit, genau an diesen Punkt in der t-Verteilung zu fallen, sofern die Nullhypothese gilt, liegt bei 0.03 – und das ist der p-Wert, also in diesem Falle eine Wahrscheinlichkeit von 0.03 oder in Prozenten ausgedrückt: 3% (sehr unwahrscheinlich). Somit hast du ein signifikantes Ergebnis, verwirfst die Nullhypothese und nimmst deine Alternativhypothese mit 5%iger Irrtumswahrscheinlichkeit an.
Weitere Verteilungen (als kleine Erinnerungsstütze):

Der p-Wert am Beispiel der Varianzanalyse
Bei einer varianzanalytischen Fragestellung wie z. B. "Wirken sich Gestalttherapie, Psychoanalyse und Verhaltenstherapie unterschiedlich auf die Lebensqualität der Patient*innen aus?" verwendest du die F-Verteilung. Als Ergebnis deiner Auswertungen (ANOVA-Tabelle) erhältst du einen F-Wert, der in der F-Verteilung liegt.
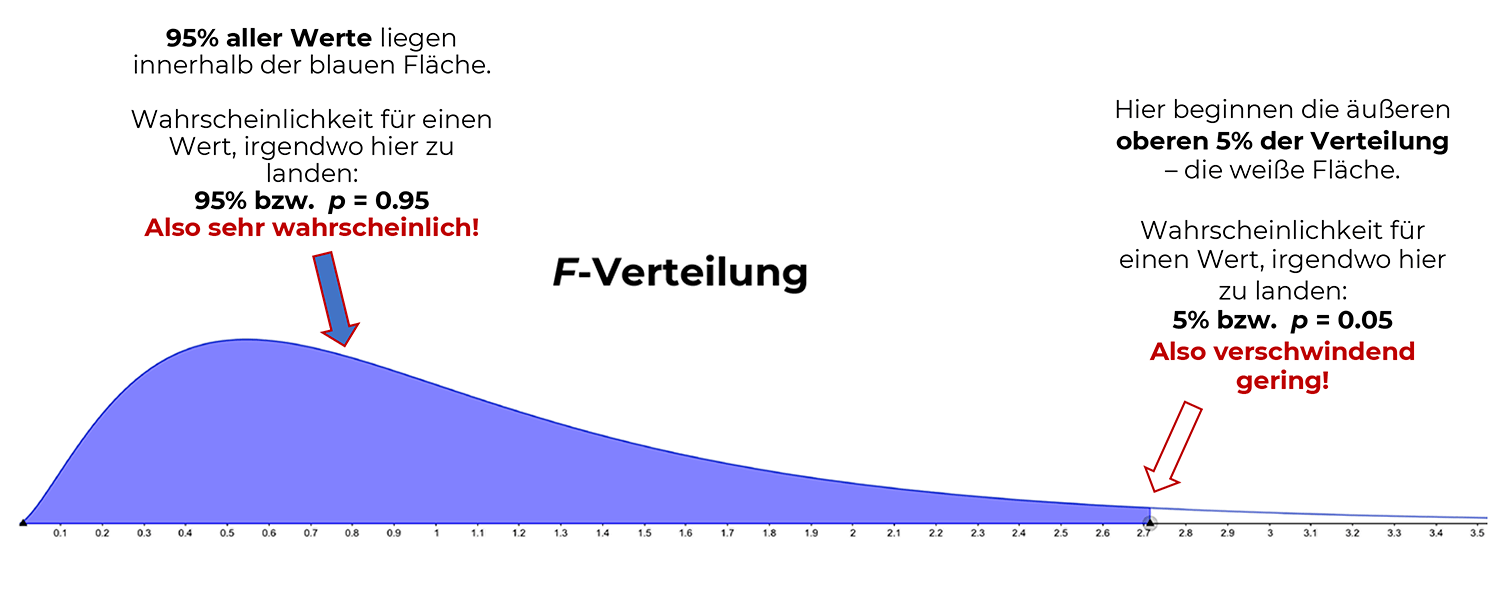
Dieser Wert fällt, wie oben beschrieben, in einen bestimmten Bereich der F-Verteilung, kommt also irgendwo unter der "Kurve" (= Dichtefunktion) zu liegen (in der Grafik stellt jetzt die weiße Fläche die äußeren 5% dar – der F-Wert ist rot abgetragen).
Du bekommst also wieder zunächst den Ergebnis-F-Wert – und dann die dazugehörige Wahrscheinlichkeit für diesen F-Wert, falls die Nullhypothese stimmt: den p-Wert.
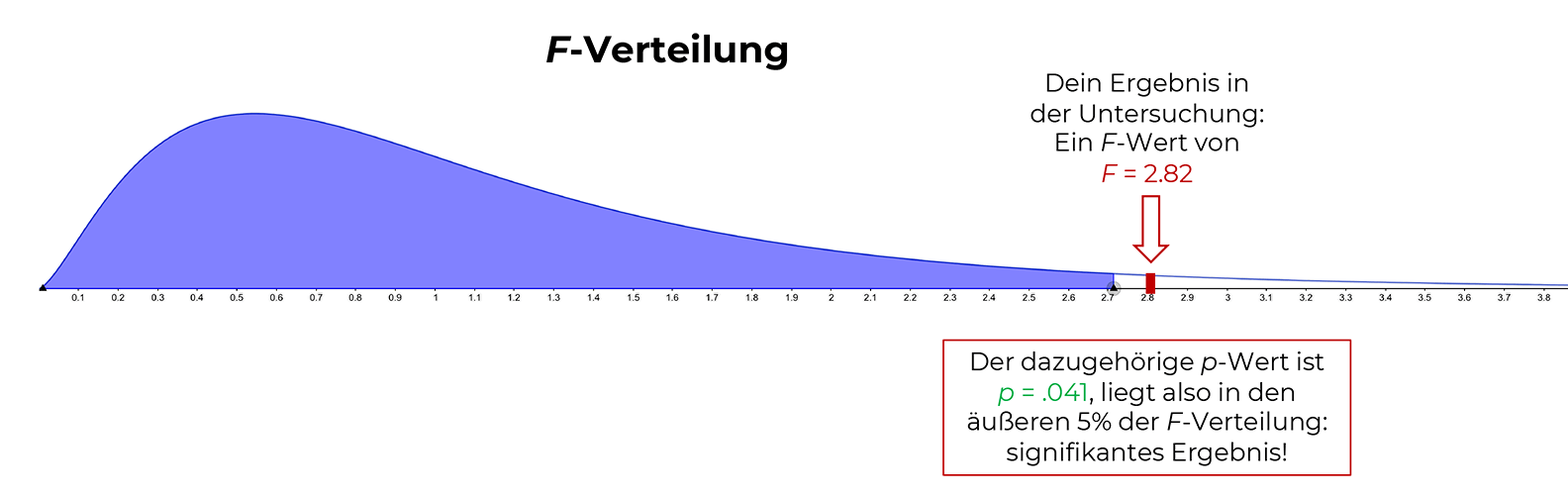
Dieser p-Wert von p = 0.041 bedeutet nichts anderes als: Das Ergebnis deiner Untersuchung fällt an den Punkt, an dem die äußeren 4.1% der Verteilung beginnen.
Anders ausgedrückt: Die Wahrscheinlichkeit für dein spezielles Ergebnis (deinen F-Wert) oder ein noch kleineres Ergebnis liegt bei 0.041 (im Alltagsjargon: bei 4.1%), wenn die Nullhypothese tatsächlich zutrifft – ist also sehr gering.
Bitte beachten:
Ich gehe hier aus Einfachheitsgründen vom üblichen Signifikanzniveau von α = 0.05 aus, also den äußeren 5% einer Verteilung.
Dies sollte jedoch bei jeder Untersuchung individuell abgewogen und festgesetzt werden!
Was hat der p-Wert mit der Signifikanz zu tun?
Liegt der p-Wert in den äußeren 5% einer Verteilung (p < 0.05), so liegt ein signifikantes Ergebnis vor!
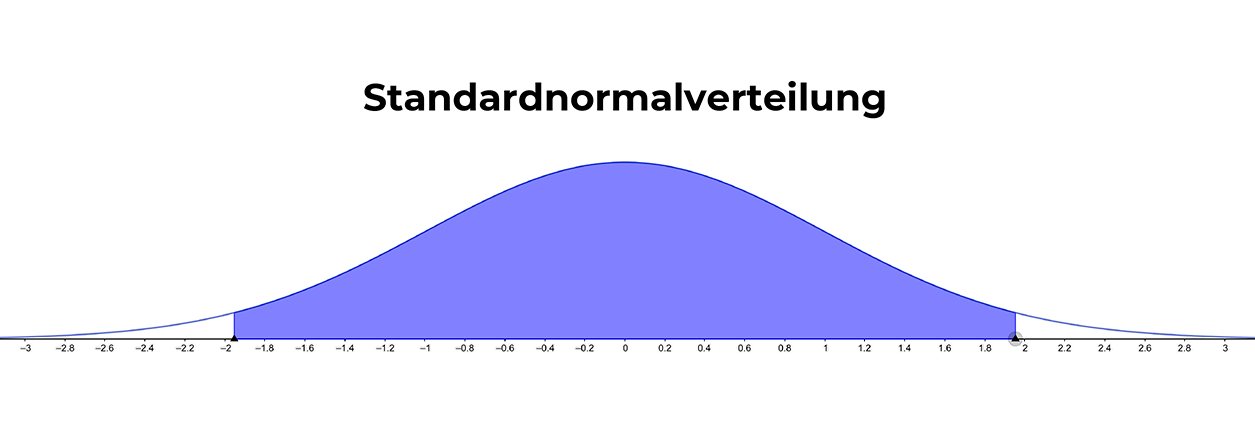
Die äußeren 5% können sich je nach Hypothese rechts, links oder beidseitig befinden – in letzterem Fall jeweils in den äußeren 2.5% auf beiden Seiten (s. Abbildung Standardnormalverteilung).
Erhält man in einer Studie ein Ergebnis bzw. einen Wert, der in die äußeren 5% einer Verteilung hineinfällt, so ist dieses Ergebnis so unwahrscheinlich, dass man sagt:
das kann kein Zufall mehr sein!
Eine solche starke Abweichung vom bisher Bekannten muss ein signifikantes Ergebnis sein!
WIE unwahrscheinlich (oder wahrscheinlich) dieses Ergebnis genau ist, sagt der p-Wert aus.
Daher lässt sich an der Höhe des p-Werts die Signifikanz ablesen:
Ist der p-Wert kleiner als 0.05, so liegt ein signifikantes (weil sehr unwahrscheinliches) Ergebnis vor.
In diesem Falle verwirfst du die Nullhypothese und nimmst deine Alternativhypothese an. Wenn dein p-Wert größer als 0.05 ist, verwirfst du deine Alternativhypothese und behältst die Nullhypothese bei.
Beispiel für den p-Wert bei SPSS: Korrelation
Der folgende Datensatz ist von Andy Field (dessen Arbeit ich sehr schätze). Du kannst dir hier ganz viele bunte Datensätze von ihm holen und damit üben.
Fragestellung in diesem Datensatz:
Kann der Verkauf von Alben einer Band (abhängige Variable bzw. Kriterium) aus den folgenden drei Variablen ( Prädiktoren) vorhergesagt werden:
Als Methode kommt hier die Regressionsanalyse zum Einsatz, da es um Vorhersagen geht.
Im ersten Output siehst du im oberen Drittel die Korrelationen (Zusammenhänge), welche die Grundvoraussetzung für die Berechnung einer Regression darstellen (Korrelationskoeffizienten r nach Bravais-Pearson = Produkt-Moment-Korrelation).
Kleiner Hinweis: In diesen Tabellen sind die Informationen jedes Abschnitts immer doppelt vorhanden – jeweils einmal oberhalb und unterhalb einer gedachten Diagonalen von links oben nach rechts unten.
Hier ist die Nullhypothese, dass es keinen Zusammenhang zwischen jeweils zwei Variablen gibt, also zwischen z. B. verkauften Alben und Band Image, zwischen Band Image und Werbe-Budget etc..
Im mittleren Bereich (bei "Sig.") findest du dazu die Auswertung (p-Werte): Sind die Korrelationen statistisch signifikant?
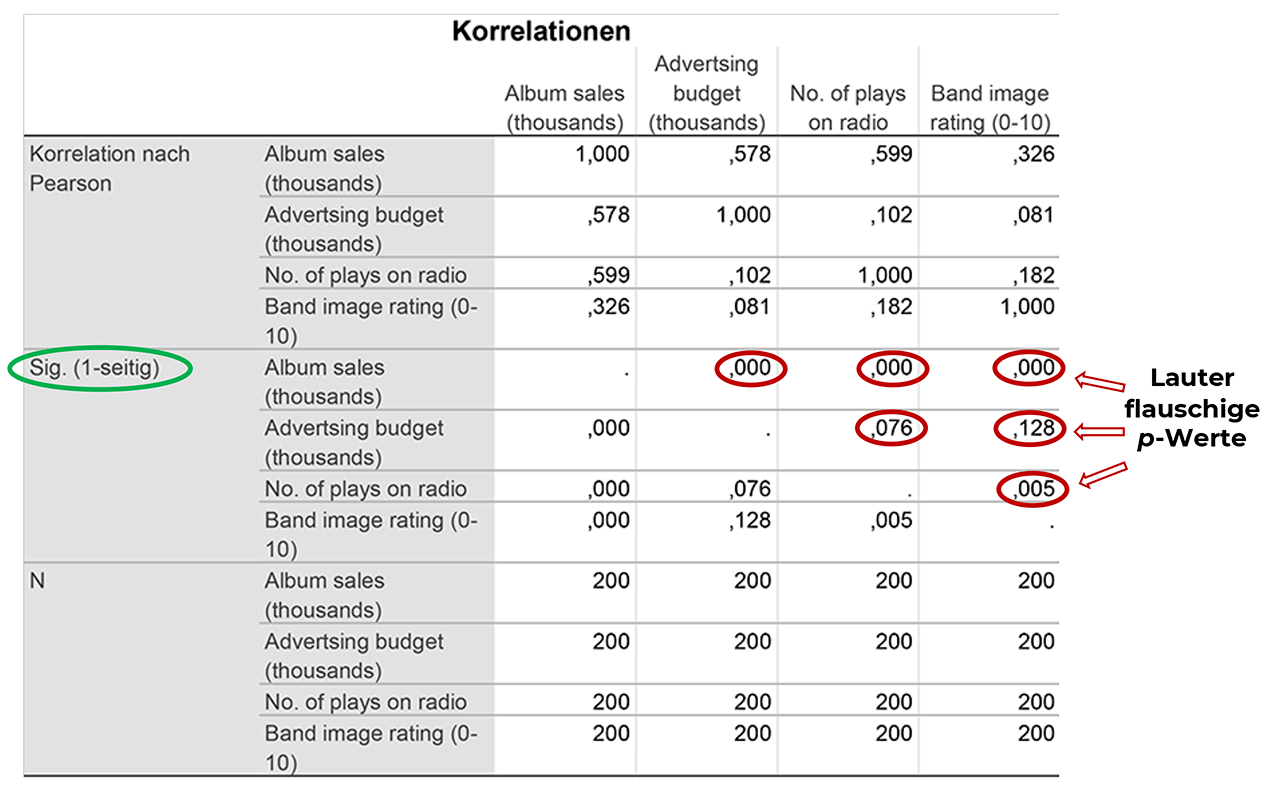
1. Zeile – Album Sales:
Hier kannst du an den aufgeführten p-Werten ablesen, dass die Anzahl an verkauften Alben signifikant mit den drei Prädiktoren korreliert: dreimal ",000" in der Zeile "Album sales".
Hinweis: Bei SPSS werden gewöhnlich immer nur die ersten drei Nachkommastellen angegeben. Irgendwann kommt dann vermutlich auch mal eine andere Zahl als Null, z. B. so was wie 0.00072134.
Die p-Werte sagen uns, dass die Wahrscheinlichkeit dafür, ein solches Ergebnis zu erhalten, wenn die Nullhypothese stimmen würde, unterhalb von 0.000% liegt. Somit ist das Ergebnis unter Gültigkeit der Nullhypothese extrem unwahrscheinlich.
Und was machen wir nun?
Richtig, wir verwerfen die Nullhypothese und nehmen die Alternativhypothese an, die da heißt:
Es gibt einen hochsignifikanten Zusammenhang (da p = 0.000) zwischen der Anzahl an verkauften Alben und jedem der drei Prädiktoren!
2. Zeile: Advertising budget:
Hier sind beide p-Werte für den Zusammenhang zwischen dem Werbe-Budget und der Anzahl an im Radio gespielten Liedern sowie dem Band-Image auf dem 5%-Niveau NICHT signifikant, da größer als p = 0.05.
Es gibt also weder einen signifikanten Zusammenhang zwischen dem Werbe-Budget und der Anzahl an im Radio gespielten Liedern noch zwischen dem Werbe-Budget und dem Band-Image. Beide dazugehörigen Nullhypothesen werden beibehalten.
3. Zeile: No. of plays on radio:
Der p-Wert von .005 zeigt einen hochsignifikanten Zusammenhang zwischen der Anzahl an im Radio gespielten Liedern und dem Band-Image.
Also verwerfen wir die Nullhypothese und nehmen die Alternativhypothese an:
Es gibt einen hochsignifikanten Zusammenhang (da p = 0.005) zwischen der Anzahl an im Radio gespielten Liedern und dem Band-Image!
Beispiel für den p-Wert bei SPSS: F-Test
Und weiter geht's: wir sind immer noch bei dem Beispiel von oben.
Im nächsten Schritt wird mit dem F-Test der Varianzanalyse überprüft, ob das Modell mit den drei Prädiktoren insgesamt etwas taugt.
Du denkst dir jetzt wahrscheinlich: "Wieso Varianzanalyse – ich dachte, wir machen eine Regression?!"
Ich gebe zu, dass das etwas verwirrend ist, aber das liegt daran, dass die Regressions- und Varianzanalyse verwandt sind und demselben mathematischen Modell entstammen, dem Allgemeinen Linearen Modell, für die Eingeweihten kurz: ALM.
Aus diesem Grund wird bei SPSS bei jeder Regression immer zunächst der F-Test der Varianzanalyse ausgegeben. Dieser wird auch "Globaler F-Test " oder "Omnibus-Test" genannt und prüft, ob das Gesamt-Modell signifikant ist.
Die Nullhypothese lautet: Keiner der Prädiktoren hat einen Einfluss auf das Kriterium, also auf die Anzahl an verkauften Alben.
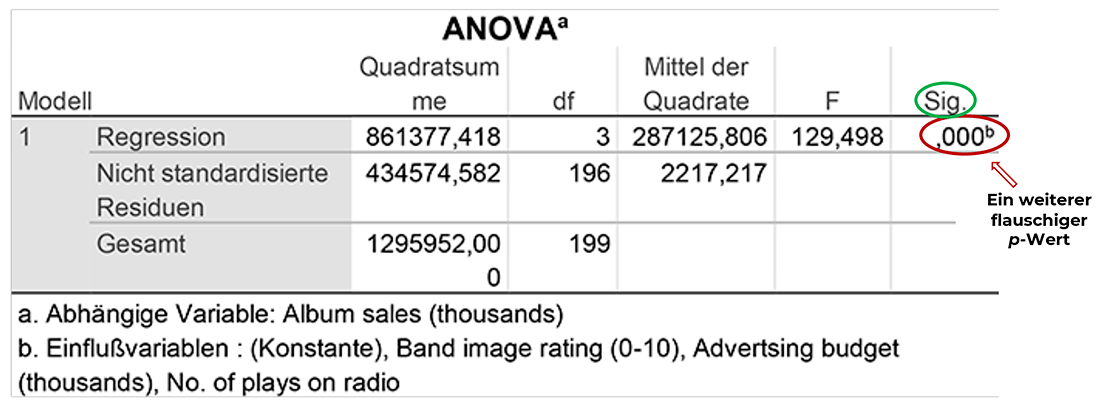
Hier sehen wir in der ersten Zeile bei "Regression" einen sehr hohen F-Wert (129.498) und den dazugehörigen p-Wert von .000.
Wir haben somit wieder ein hochsignifikantes Ergebnis und können davon ausgehen, dass das Regressions-Modell mit den drei Prädiktoren insgesamt etwas taugt.
Also verwerfen wir die Nullhypothese und nehmen die Alternativhypothese an, die in diesem Falle lautet:
Mindestens einer der Prädiktoren hat einen Einfluss auf die Anzahl an verkauften Alben!
Welcher das ist bzw. welche das sind, sieht man dann in der Ergebnistabelle mit dem Namen "Koeffizienten", die hier jedoch nicht mehr aufgeführt ist. Falls dich das interessiert, kannst du dir einfach diesen Datensatz holen (oder einen anderen Regressions-tauglichen) und die Tabelle von SPSS ausspucken lassen.
Zusammenfassung
Geschafft!

Hut ab! Tapfer durchgehalten, wenn du bis hierher gelesen hast.
Ich hoffe, dass du jetzt für künftige Interpretationen des p-Werts gut gerüstet bist!
Probier's doch gleich mal aus: Lad' dir ein paar Datensätze runter und spiel damit!
Denn: Statistik darf tatsächlich Spaß machen!
auch wenn das erst mal kontraintuitiv erscheint...
QUELLEN (Als Amazon-Partnerin verdiene ich an qualifizierten Verkäufen):
Bortz, J., & Schuster, C. (2017). Statistik für Human- und Sozialwissenschaftler. Berlin: Springer.
Field, A. (2018). Discovering Statistics using IBM SPSS Statistics. London: SAGE.

Vielen lieben Dank für diesen Beitrag! Die vielen verschieden Vorgehensweisen im Internet zur Ermittlung des P-Werts über SPSS haben mich extrem verwirrt!
Ich konnte leider aus Ihrem Post nicht herauslesen, welchen P-Wert ich am Ende bei der Auswertung in meiner Thesis angebe. Den P-Wert in der Korrelationstabelle oder ANOVA?
VG Larissa
Hallo liebe Larissa,
das hängt ganz davon ab, was du untersuchst.
Du gibst immer den p-Wert an, der zu deiner jeweiligen Fragestellung und Methode gehört.
Wenn du sowohl eine Korrelation als auch eine ANOVA rechnest, musst du beide p-Werte angeben.
Liebe Grüße!