SPSS Outputs lesen leicht gemacht! Teil 2: Zusammenhangsmaße
Neue Runde, neues Glück! Nachdem wir uns in Teil 1 tapfer durch die deskriptiven Statistiken (inkl. Chi-Quadrat) kämpften, geht es nun mit Zusammenhangsmaßen für ordinalskalierte und metrische Variablen weiter, gefolgt von der Prüfung auf Normalverteilung der Daten. Letzteres ist ein wesentlicher Baustein deiner Statistik-Toolbox, da die meisten Verfahren in der Psychologie auf der Annahme von Normalverteilung beruhen. Und da wär's ganz gut, wenn du wüsstest, wie man das macht.
Damit du alles selbst nachvollziehen kannst, schreibe ich dir wieder die jeweiligen Schritte dazu, um die abgebildeten Ergebnistabellen zu erhalten.
Dabei gehe ich davon aus, dass du statistisches Vorwissen hast und dich mit der grundsätzlichen Bedienung von SPSS auskennst. Natürlich kannst du dir alles auch nur so durchlesen, ohne die Daten selbst aufzurufen.
Hast du was anderes gesucht? Klick' hier für SPSS für die deskriptive Statistik, hier für t-Test und Regression sowie hier für die Varianzanalyse.
Wo du Datensätze zum Üben herbekommst
Datensätze bekommst du auf verschiedensten Seiten im Internet sowie direkt im Programm SPSS. Ich empfehle z. B. die Datensätze von Andy Field, die hier zu finden sind.
Praktischerweise liefert SPSS aber auch eine Fülle von Datensätzen mit, die du folgendermaßen erreichen kannst:
Windows: C:/Programme/IBM/SPSS/Statistics/27 (oder eine andere Version)/Samples/German
Mac: Im Finder: Applications oder Programme/IBM/SPSS/Statistics/27 (oder eine andere Version)/Samples/German
Zusammenhangsmaße für ordinalskalierte Daten
Die nachfolgenden Outputs entstammen alle dem Datensatz survey_sample.sav im SPSS-Samples-Folder, der knackige 46 Variablen und 2.832 Fälle aus den USA enthält. Bitte suche und öffne ihn – und los geht's.
Hier gibt es, wie so oft bei SPSS, zwei Wege zum Glück. Ich zeige dir zunächst die Variante über den Weg, den du bereits aus Teil 1 kennst.
Gehe auf "Analysieren", "Deskriptive Statistiken", "Kreuztabellen". Im sich öffnenden Fenster klickst du die beiden ordinalskalierten Variablen "Höchster Abschluss" (Zeilen) sowie "Allgemeine Zufriedenheit" (Spalten) an. Es macht für das Ergebnis übrigens keinerlei Unterschied, welches Merkmal du den Zeilen oder Spalten zuordnest.
Jetzt klickst du auf das Kästchen "Statistiken" auf der rechten Seite und setzt bei "Kendalls-Tau-b" einen Haken (auf gar keinen Fall zu verwechseln mit Kendalls-Tau-c ; ) – hier braucht es mal wieder Humor, um nicht zu verzweifeln...), drückst auf "weiter" und dann auf "OK". Du erhältst den nachfolgenden Output.
Was du hier ablesen kannst, ist Folgendes:
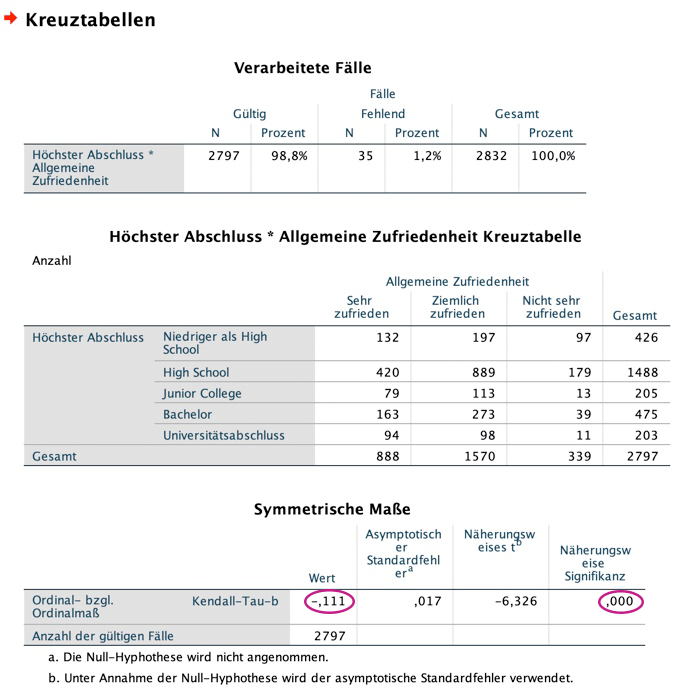
aber aufgepasst:
Immer die Operationalisierung bzw. Kodierung der Variablen in der Datenansicht ansehen!
Sonst besteht die gefahr einer fehlinterpretation.
Würden wir uns die Kodierung nicht ansehen und einfach davon ausgehen, dass sowohl bei "Höchster Abschluss" als auch bei "Allgemeine Zufriedenheit" höhere Werte automatisch einen höheren Abschluss bzw. mehr Zufriedenheit bedeuten, würden wir, wie oben erfolgt, das Ergebnis falsch interpretieren.
Ein Blick in die Daten verrät nämlich, dass höheren Abschlüssen wie erwartet höhere Zahlen zugeordnet wurden – wohingegen die Zufriedenheit gegenläufig kodiert ist: 1 ist "Sehr zufrieden" und 3 "Nicht sehr zufrieden". Guckst du: geh' in die Datenansicht, such' die interessierenden Variablen und klick' in der Spalte "Werte" das Kästchen mit den drei Punkten an. Dann erhältst du die folgenden Fenster:
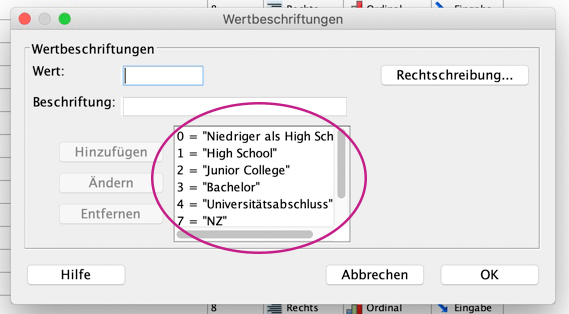
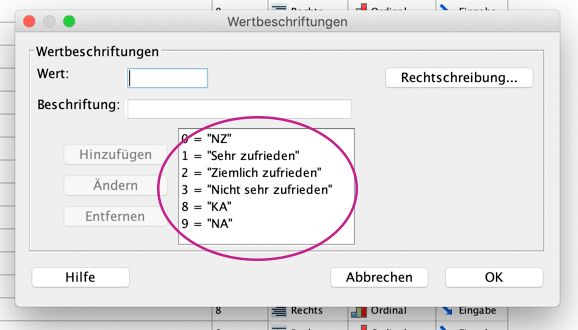
Alternativer Weg zu Zusammenhangsmaßen für ordinalskalierte Daten
Gehe auf "Analysieren", "Korrelation", "Bivariat". Im sich öffnenden Fenster klickst du wieder die beiden ordinalskalierten Variablen "Höchster Abschluss" sowie "Allgemeine Zufriedenheit" an und verschiebst sie in das Feld "Variablen".
Jetzt setzt du darunter bei "Korrelationskoeffizienten" bei Kendall-Tau-b sowie Spearman einen Haken (und nimmst den Haken bei Pearson raus), drückst auf "weiter" und dann auf "OK". Du erhältst folgenden Output:
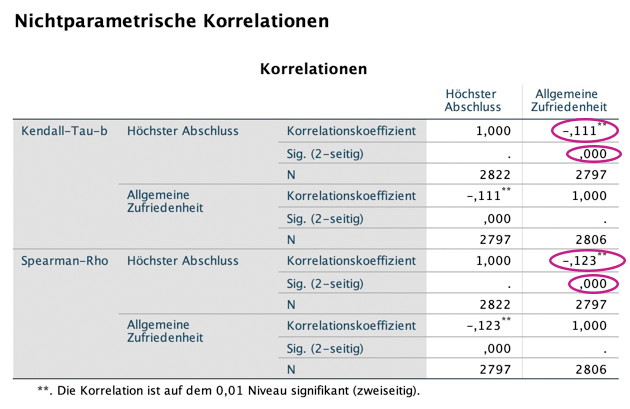

Zusammenhangsmaße bei metrischen Variablen
Zum Abschluss des bunten Korrelationsreigens wollen wir uns das wohl am häufigsten verwendete Zusammenhangsmaß ansehen: den Korrelationskoeffizienten r nach Bravais-Pearson – oder auch Produkt-Moment-Korrelation genannt.
Gehe dazu wieder auf "Analysieren", "Korrelation", "Bivariat". Im sich öffnenden Fenster klickst du jetzt zwei metrische Variablen an, nämlich "Alter" (Verhältnisskala) und "Wie viele Stunden Fernsehen pro Tag" (Absolutskala) und verschiebst sie in das Feld "Variablen".
Da "Pearson" schon blau markiert erscheint, drückst du einfach nur auf "OK" und erhältst den nachfolgenden Output.

Was du hier ablesen kannst, ist Folgendes:

Prüfung auf Normalverteilung der Daten
Die meisten Verfahren innerhalb der Psychologie beruhen auf der Annahme bzw. Voraussetzung, dass die Daten normalverteilt sind. Ob dem jedoch tatsächlich so ist, lässt sich mit SPSS ganz einfach überprüfen.
Gehe dazu auf "Analysieren", "Deskriptive Statistiken", "Explorative Datenanalyse". Im sich öffnenden Fenster wählst du wieder die Variablen "Alter" und "Wie viele Stunden Fernsehen pro Tag" aus und verschiebst sie in das Feld "Abhängige Variablen" (da die Normalverteilung eine stetige Verteilung ist, wählen wir hier metrische, stetige Variablen aus).
Jetzt klickst du rechts auf "Diagramme" und setzt bei "Normalverteilungsdiagramm mit Tests" einen Haken, drückst auf "weiter" und dann auf "OK". Du erhältst den nachfolgenden Output.

Was du hier ablesen kannst, ist Folgendes:
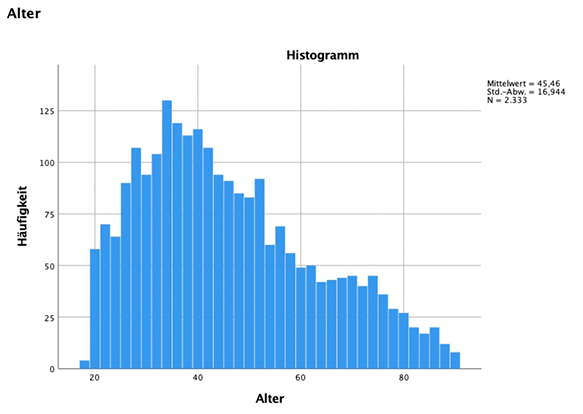
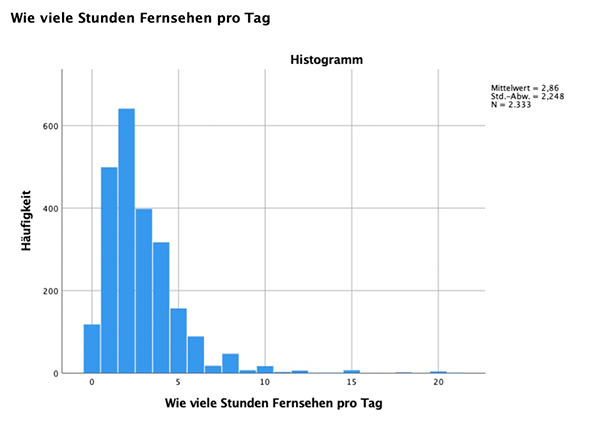
Grafische Überprüfung, ob Normalverteilung vorliegt
Um dir die Ergebnisse der Tests auf Normalverteilung auch noch grafisch anzusehen, geh' auf "Analysieren", "Deskriptive Statistiken", "Explorative Datenanalyse", gib wieder die beiden Variablen ein und drück' rechts auf "Diagramme". Dort kannst du rechts unterhalb von "Stamm-Blatt" bei "Histogramm" einen Haken setzen.
Du erhältst folgende Diagramme, bei denen sofort erkennbar ist, dass keine Normalverteilung vorliegt, da sie keine symmetrische Glockenform aufweisen:
Fühlst du dich lost im dschungel der Statistischen methoden?
Dann schnapp' dir das E-Book (0,-€):
endlich durchblick in statistik!
in 4 einfachen schritten zur wahl der richtigen methode

Geschafft!
So, das war's für Teil 2! Ich hoffe, es fällt dir nun etwas leichter, dich in den Ergebnistabellen zurechtzufinden! Vielleicht hast du ja sogar Lust, dir gleich einen weiteren Datensatz zu schnappen und das Ganze anzuwenden.
Jetzt ist aber erst mal Zeit für Donuts!

KENNST DU SCHON MEINEN YOUTUBE-KANAL?

Guckst du hier:

