In der Psychologie und den meisten Sozialwissenschaften können wir immer nur Stichproben aus der interessierenden Grundgesamtheit ziehen und so gut wie nie alle in Betracht kommenden Personen befragen/testen/beobachten. Daher müssen wir uns mit den Ergebnissen aus einer Stichprobe begnügen und von diesen auf die dazugehörige Grundgesamtheit schließen.
Um das tun zu können, gibt es verschiedene Vorstellungen davon, wie Variablen wie z. B. Neugier, Offenheit für neue Erfahrungen oder Resilienz verteilt sein könnten, d. h. in welchem Bereich sich wohl die meisten Werte tummeln und wie wahrscheinlich es ist, dass eine Person aus der betreffenden Grundgesamtheit einen Wert hat, der in ein bestimmtes Intervall fällt.
Und genau dafür gibt es die Dichtefunktion: sie ist eine visuelle Darstellung der Auftretenswahrscheinlichkeiten von bestimmten Ausprägungen einer Variablen.
Was ist eine Dichtefunktion?
Zunächst ein Beispiel: Angenommen, dich interessiert die Kompromissfähigkeit bei gewaltbereiten Jugendlichen auf einer Skala von 0 (= gar nicht vorhanden) bis 100 (= super stark ausgeprägt). Damit hättest du eine stetige, metrische Variable (auf Intervallskalenniveau).
"Stetig" bedeutet, dass zwischen zwei Merkmalsausprägungen THEORETISCH unendlich viele Werte liegen können, wenn man nur genau genug messen würde. Merk' dir vielleicht einfach, dass du bei stetigen Variablen potenziell immer ein Komma und unendlich viele Nachkomma-Stellen anhängen könntest. Also bei der Kompromissfähigkeit so was wie: 48,897120823546043745654...
Nun möchtest du womöglich wissen, wo sich die meisten Werte herumtreiben und wie wahrscheinlich es ist, dass ein Jugendlicher z. B. eine Kompromissfähigkeit zwischen 35 und 40 aufweist. Ersteres kannst du in der Dichtefunktion SEHEN, Letzteres mit der Verteilungsfunktion BERECHNEN.
Eine Dichtefunktion oder Wahrscheinlichkeitsdichte ist eine schicke visuelle Darstellung der Verteilung von stetigen Variablen. Sie zeigt dir, wie und wo sich die einzelnen Merkmalsausprägungen auf einer Skala verteilen und in welchem Bereich die meisten Werte auftreten.
Dort, wo sich die meisten Werte ballen, besteht auch die höchste Wahrscheinlichkeit dafür, dass eine zur interessierenden Grundgesamtheit gehörige (z. B. gewaltbereite Jugendliche), zufällig ausgewählte Person hier ihre Ausprägung hat. Bei der Normalverteilung ist das um den Mittelwert herum.
Hier siehst du die Dichtefunktion einer Normalverteilung zum Kompromissfähigkeits-Beispiel mit einem Mittelwert von 35 und einer Standardabweichung von 8. Der Bereich +/– eine Standardabweichung ist blau markiert – dort finden sich die meisten Werte. Daher ist auch die Wahrscheinlichkeit am höchsten, dass ein zufällig ausgewählter gewaltbereiter Jugendlicher hier seinen Wert hat, nämlich zwischen 27 und 43.

In welchen Bereich der Statistik gehört sie?
Die Dichtefunktion gehört in die Welt der Inferenzstatistik und dort in den Bereich des theoretischen Grundwissens.
Dieses Wissen brauchst du, um zu verstehen, wie die verschiedenen Verteilungen zustande kommen (z. B. t oder F), was man mit ihnen machen kann und wie man Wahrscheinlichkeiten berechnet.
Wie entsteht die Dichtefunktion?
Stell' dir vor, man würde zur Kompromissfähigkeit von gewaltbereiten Jugendlichen unendlich viele Untersuchungen machen und immer wieder Stichproben aus derselben Population ziehen.
Wenn man dann bei jeder dieser Untersuchungen z. B. den Mittelwert berechnen und diesen auf der oben genannten Skala zwischen 0 und 100 mit einem Strich aufzeichnen würde, bekäme man (sehr vereinfacht gesagt) mit der Zeit aus ganz, ganz vielen Strichen eine Fläche. Dort, wo die Werte besonders oft hinfallen, wo also Ballungen entstehen, häufen sich die Striche, werden länger und es entsteht eine Art Hügel oder Kurve.
Diese Kurve bzw. Dichtefunktion zeigt nun, an welcher Stelle sich die meisten Werte ansammeln und wie wahrscheinlich Merkmalsausprägungen in bestimmten Bereichen sind. Wo die Kurve am höchsten ist, ist auch die Wahrscheinlichkeit am höchsten, dass jemand dort seine Merkmalsausprägung hat.
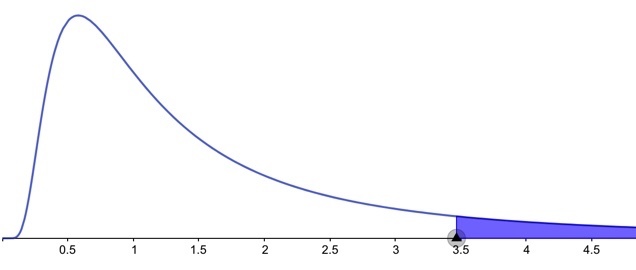
Die Dichtefunktion muss jedoch nicht immer wie Schlange-frisst-Elefant aussehen.
Hier siehst du ein Beispiel der Dichtefunktion einer F-Verteilung – das ist die Verteilung, die du z. B. für die Varianzanalyse und Regression brauchst:
Eigenschaften der Dichtefunktion
Zum Abschluss noch ein kleiner Steckbrief:
Steckbrief Dichtefunktion
Quellen:
Bortz, J., & Schuster, C. (2017). Statistik für Human- und Sozialwissenschaftler. Springer.
Field, A. (2018). Discovering Statistics using IBM SPSS Statistics. SAGE.
Sedlmeier, P., & Renkewitz, F. (2018). Forschungsmethoden und Statistik für Psychologen und Sozialwissenschaftler. Pearson.
