Cohens d ist quasi ein Dauerbrenner in der Statistik und wird dir im Verlauf deines Studiums immer wieder begegnen.
Es ist ein Effektstärkemaß (dazu gleich mehr), das dir zeigt, wie groß ein gefundener Effekt bei Mittelwertsunterschieden ist.
Das wäre z. B. eine Fragestellung wie: "Unterscheiden sich Frauen und Männer in ihrem Shopping-Durchhaltevermögen?".
Wenn du diese Studie machen würdest, würdest du zunächst einen t-Test für unabhängige Stichproben durchführen und dann schauen, ob du ein signifikantes Ergebnis erhältst.
Anschließend stellt sich dann die Frage, wie groß der gefundene Mittelwertsunterschied zwischen den beiden Gruppen ist und in welche Richtung er geht. Wobei wir hier vermutlich auch ohne Daten so unsere Vermutungen hätten....
Im Folgenden zeige ich dir, wie du nach einem signifikanten Hypothesentest durch die Berechnung von Cohens d eine Aussage über die praktische Relevanz des gefundenen Effekts machen kannst.
Da es für dieses Effektstärkemaß verschiedene Varianten gibt (man mag es in der Statistik ja gerne etwas kompliziert), dreht sich dieser Artikel ausschließlich um Cohens d zum Unterschied zweier Mittelwerte aus unabhängigen Stichproben.
"Unabhängige Stichproben" meint, dass bei allen Proband*innen nur einmal der interessierende Wert erhoben wurde.
Was sind Effektstärken?
Effektstärken bzw. Effektstärkemaße zeigen, wie stark ein in einer Studie beobachteter Effekt ist.
Je nach Inhalt der Untersuchung verwendet man unterschiedliche Effektstärkemaße. Diese werden in zwei Gruppen eingeteilt: Abstandsmaße und Zusammenhangsmaße.
Erstere zeigen meist die Größe der Abstände zweier Mittelwerte in Standardabweichungs-Einheiten an, während Letztere gewöhnlich Variationen des Korrelationskoeffizienten r nach Bravais-Pearson sind. Schickerweise lassen sich beide Gruppen ineinander überführen!
In welchen Bereich der Statistik gehören sie?
Die Effektstärken gehören in die Welt der schließenden oder Inferenzstatistik, können jedoch auch deskriptivstatisch verwendet werden – also nur zur Beschreibung dessen, was bei bestimmten Stichproben vorgefunden wird, ohne auf die dazugehörige Grundgesamtheit schließen zu wollen.
Im Bereich der Inferenzstatistik sollten sie zusätzlich zur Angabe des Ergebnisses eines Signifikanztests mit angegeben werden.
Was sagt Cohens d aus?
Cohens d ist eines der am häufigsten in der Statistik verwendeten Effektstärkemaße und beschreibt, wie stark sich die Mittelwerte zweier Stichproben unterscheiden.
Da Cohens d ein standardisiertes Abstandsmaß ist, ist es unerheblich, mit welchen Messinstrumenten die abhängige Variable erhoben wurde. Denn durch die Standardisierung werden evtl. mit verschiedenen Messinstrumenten gemessene Mittelwerte auf eine neue, gemeinsame dimensionslose Einheit gebracht und dadurch direkt vergleichbar.
Ein weiterer Vorteil ist, dass Cohens d im Gegensatz zum p-Wert nicht von der Stichprobengröße abhängt.
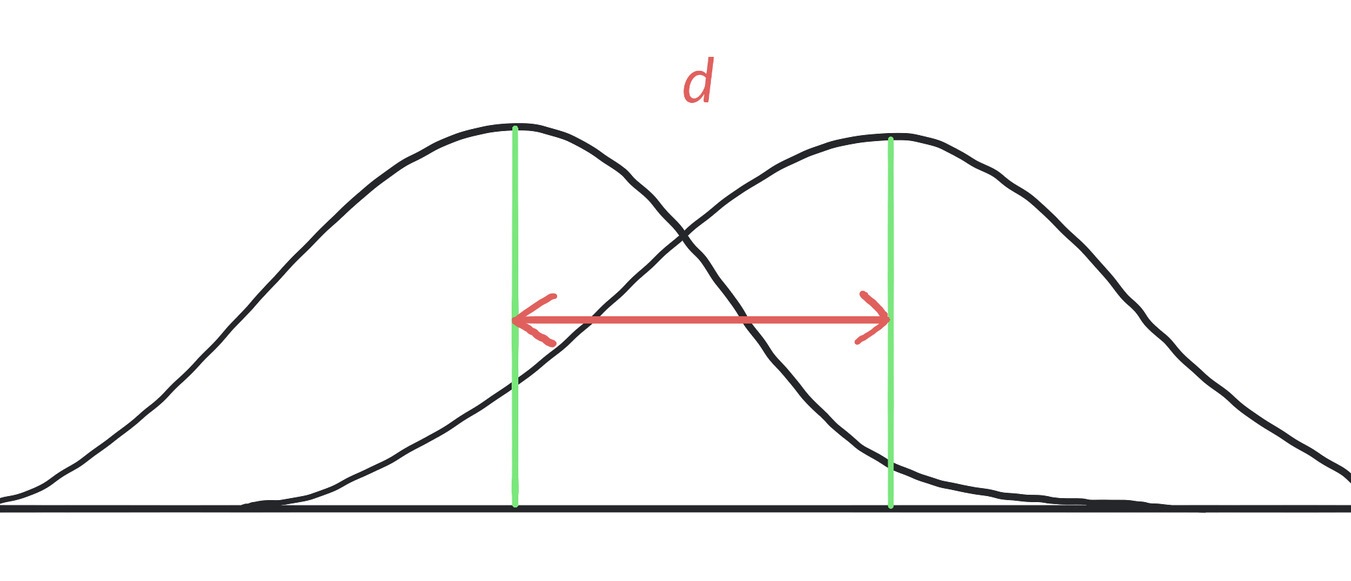
Grafisch dargestellt bedeutet der Mittelwertsunterschied, wie weit die beiden Mittelwerte auf der x-Achse auseinander liegen. Je näher, desto kleiner d – und je weiter auseinander, desto größer d und somit der gefundene Effekt.
Guckst du – hier liegen die Mittelwerte relativ weit auseinander, so dass vermutlich ein mittlerer Effekt vorliegt. Ob dieser Effekt groß genug ist, um statistisch signifikant zu sein, muss man jedoch berechnen.
Berechnung Cohens d
Hier ist die Formel, um den standardisierten Mittelwertsunterschied bei zwei unabhängigen Stichproben zu berechnen.
Wir machen das jetzt zur oben erwähnten Fragestellung zum Unterschied des Shopping-Durchhaltevermögens von Frauen und Männern. Das Shopping-Durchhaltevermögen wird auf einer Skala von 0 (= gar nicht vorhanden) bis 100 (= stolze*r Preisträger*in der platinfarbenen Einkaufstasche) erhoben.
Die unten abgebildete Formel besteht im Zähler aus dem Abstand zwischen den beiden Mittelwerten, der dann anhand der gemeinsamen Streuung im Nenner relativiert und somit standardisiert wird. Da gewöhnlich von Stichproben-Mittelwerten ("x quer") auf die Erwartungswerte in der Population ("mü") geschlossen wird, verwendet man in der Praxis den zweiten, rechten Teil der Formel:
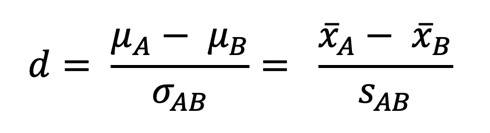
Angenommen, wir hätten aus unseren Daten Folgendes errechnet:
- für die Frauen (Gruppe A) einen Mittelwert von 65.3 mit einer Standardabweichung von 4.5
- für die Männer (Gruppe B) einen Mittelwert von 59.6 mit einer Standardabweichung von 3.9
Die Mittelwerte für den Zähler haben wir nun schon, jetzt fehlt uns nur noch die gemeinsame Streuung für den Nenner. Dafür gibt es zwei Varianten:
GLEICHE STICHPROBENGRÖßEN IN BEIDEN GRUPPEN
Wenn die Stichprobengröße bei beiden Gruppen gleich ist, verwendest du die folgende Formel für die Berechnung der gemeinsamen Streuung:
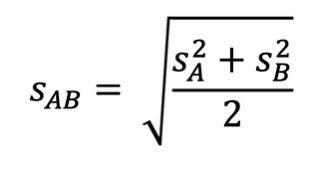
Wenn wir beispielsweise eine Stichprobengröße von 60 Personen in beiden Stichproben (= gleiche Anzahl von Personen in jeder Gruppe) haben, sieht die obige Formel nun so aus:
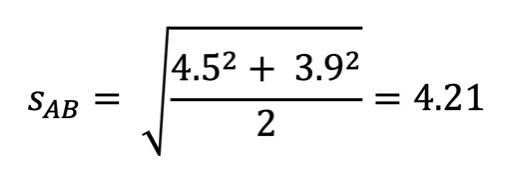
Jetzt können wir alle Werte in die oberste Gleichung einsetzen und erhalten d:
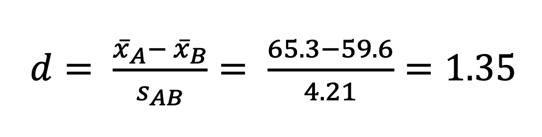
Gemäß den Konventionen von Cohen (s. u.) wäre das ein ausgesprochen starker und praktisch bedeutsamer Mittelwertsunterschied!
UNGLEICHE STICHPROBENGRÖßEN IN BEIDEN GRUPPEN
Ist hingegen die Stichprobengröße ungleich, nimmst du diese schöne Formel für die gemeinsame Streuung:
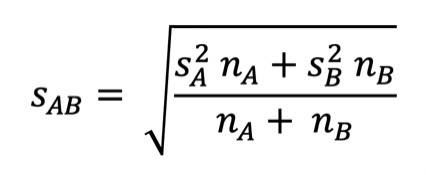
Bei Stichprobengrößen von 58 Frauen (Gruppe A) und 51 Männern (Gruppe B) sieht das dann so aus:
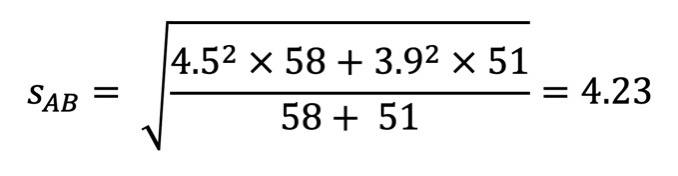
In die Ursprungsformel eingesetzt:
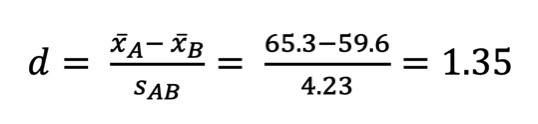
FAZIT:
In diesem Fall bleibt die Aussage gleich, da sich durch die unterschiedlichen Stichprobengrößen nichts verändert hat (dies ist jedoch nicht immer so).
Es liegt hier also ein ausgesprochen starker Mittelwertsunterschied vor, d. h. Männer und Frauen unterscheiden sich sehr stark in ihrem Shopping-Durchhaltevermögen (wer hätte das gedacht!).
Die Frauen sind um 1.35 Standardabweichungen durchhaltefähiger als die Männer!
Brauchst du hilfe beim lernen von statistik?
Dann komm zu statistik-gym,
dem Online-Fitnessstudio für Statistik,
das dich fit für die Prüfung macht!
Eine Mitgliedschaft wie im Fitness-Studio oder bei Streaming-Anbietern, nur eben für Statistik im Bachelor,
die dir hilft, dieses Fach endlich zu verstehen & die Prüfung zu meistern!
Darin bekommst du:
Und dann macht Statistik vielleicht sogar Spaß!
Klingt gut? Dann klick hier:
Konventionen für die Interpretation
Praktischerweise gibt es für die Interpretation der Mittelwertsunterschiede von J. Cohen (1988) vorgeschlagene Konventionen, welche als grober Anhaltspunkt zu verstehen sind:
Die Striche um das d herum sind Betragstriche, was bedeutet, dass der Wert z. B. –0.2 oder +0.2 sein kann. Cohens d kann also auch negativ werden.
Da es sich hierbei um Konventionen bzw. Orientierungspunkte handelt, sollte man die in einem Forschungsbereich typischen Effekte bei der Interpretation mit einbeziehen.
Schau dir also vor der finalen Einschätzung der Stärke des gefundenen Effekts verschiedenen Studien zu deinem Thema an, um ein Gefühl dafür zu bekommen, was in dem jeweiligen Feld als "kleiner", "mittlerer" oder "großer" Effekt bezeichnet werden kann.
Cohens d mit SPSS & Online-Rechnern
SPSS spuckt d erst ab Version 27 mit aus.
Falls du eine niedrigere Version hast oder gar nicht mit SPSS arbeitest, gibt's Psychometrica, eine wunderbare und sehr hilfreiche Seite zur Berechnung diverser statistischer Kennzahlen.
Mehr zum Cohens d und generell zur Inferenzstatistik findest du in meinem ganz wunderbaren
Buch "Schließende Statistik einfach erklärt! Von Null auf Statistik-Profi mit Schritt-für-Schritt-Anleitungen",
Zum Abschluss noch ein Steckbrief:
Steckbrief Cohens d
Geschafft – Respekt!
Wenn du einen Beispiel-Datensatz zur Hand hast (z. B. von Andy Field), dann versuch dich doch gleich mal an der Berechnung von d und überprüf deine Ergebnisse bei Psychometrica, R oder SPSS!
Und jetzt: fette Belohnen!
Statistik ist ja gemeinhin nicht das allerflauschigste Fach.
Also sollten wir es uns zumindest beim und nach dem Lernen gut gehen lassen...
Quellen (Als Amazon-Partnerin verdiene ich an qualifizierten Verkäufen):
Bühner, M., & Ziegler, M. (2017). Statistik für Psychologen und Sozialwissenschaftler. Pearson.
Field, A. (2018). Discovering Statistics using IBM SPSS Statistics. SAGE.
Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed). Hillsdale, N.J: L. Erlbaum Associates.
Ellis, P. D. (2010). The Essential Guide to Effect Sizes: Statistical Power, Meta-Analysis, and the Interpretation of Research Results. Cambridge: Cambridge University Press.