Standardabweichung & Varianz einfach erklärt!
An Standardabweichung und Varianz kommt niemand vorbei, der oder die Statistik lernt. Sie gehören zur statistischen Grundausstattung und laufen einem immer wieder über den Weg, egal ob in der deskriptiven oder der schließenden Statistik (ich sage nur: Varianzanalyse...).
Beide zeigen, wie weit die Daten um den Mittelwert herum streuen, wobei nur die Standardabweichung praktisch interpretierbar ist und die typische Abweichung vom "Durchschnitt" anzeigt.
Im Folgenden lernst du, wie du diese beiden Kennwerte berechnest und interpretierst!
Was sind Standardabweichung & Varianz?
Die Standardabweichung ist die Wurzel aus der Varianz und somit quasi ihre "Tochter".
Beide beschreiben bzw. quantifizieren die Streuung der Werte um den Mittelwert eines Datensatzes herum, geben also Auskunft darüber, wie sehr sich die Versuchspersonen im betreffenden Merkmal unterscheiden. Sie können nur bei metrischen Daten angewendet werden – bei Intervall-, Verhältnis- oder Absolutskala (falls dir das nichts sagt, guckst du hier).
Diese Streuungs- oder Dispersionsmaße sind in jeder empirischen Studie zu finden – meist wird die Standardabweichung als Zusatzinformation zum Mittelwert angegeben. Das sieht dann folgendermaßen aus: M (SD) – z. B. 5.14 (2.36) –, wobei M der Mittelwert ist (mean) und SD das Akronym für die Standardabweichung (standard deviation).
Der große Unterschied zwischen beiden ist, dass bei der Varianz die Werte im Quadrat vorliegen und bei der Standardabweichung in den Original-Einheiten. Beispielsweise macht die Aussage "Neurotizismus im Quadrat" (= Varianz beim Merkmal Neurotizismus) im Alltag bzw. umgangssprachlich durchaus Sinn, statistisch hingegen nicht.
Daher dient die Varianz als rechnerische Brücke, um zur Standardabweichung zu kommen, welche für die konkrete Interpretation um einiges userfreundlicher ist. Zudem stellt die Varianz die Basis für weitergehende Berechnungen dar, z. B. bei der Regression oder – man hätte es fast vermutet – der Varianzanalyse.
In welchen Bereich der Statistik gehören sie?
Standardabweichung und Varianz gehören in die Welt der beschreibenden oder deskriptiven Statistik, sind jedoch auch in der schließenden Statistik anzutreffen – sie heißen dann nur ein wenig anders: Aus s (Standardabweichung) und s Quadrat (Varianz) werden auf Populationsebene dann Sigma und Sigma Quadrat. Das Prinzip bleibt jedoch das gleiche.
Was sagt die Standardabweichung aus?
Die Standardabweichung beschreibt bzw. quantifiziert, wie weit die Werte typischerweise um den Mittelwert eines Datensatzes herum streuen: wie groß eine typische, repräsentative Abweichung vom "Durchschnitt" ist.
Wenn in den Daten Normalverteilung vorliegt, liegen knapp 70% aller Werte zwischen einer Standardabweichung unterhalb und einer Standardabweichung oberhalb des Mittelwerts.
Die Varianz sollte, wie oben bereits beschrieben, nicht zur Interpretation verwendet werden, sondern nur als Brücke, um zur Standardabweichung zu gelangen.
Berechnung Varianz
Was wäre die Statistik ohne wunderschöne Formeln? Hier siehst du zunächst die Formeln, bevor ich dir erkläre, was du damit machst.
Diese Formel verwendest du, wenn du aus der Stichprobe die tatsächlich in der Population geltende Varianz berechnen willst – das ist die sog. "Stichprobenvarianz":
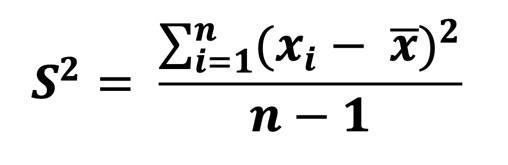
ODER, auch gerne genommen (ist beides irgendwie hübsch), falls du einfach nur die Varianz in deiner Stichprobe berechnen willst, ohne auf die Grundgesamtheit zu schließen: "empirische Varianz"
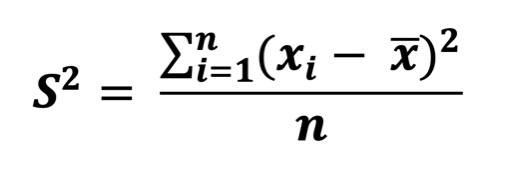
Je nach Lehrbuch findest du die eine oder die andere Variante. Wenn man durch "n - 1" teilt, kommt man näher an die in der Grundgesamtheit (= Population) geltende Varianz heran.
So gehst du vor:
- Berechne den Mittelwert
- Ziehe von jedem Wert den Mittelwert ab und setze das Ergebnis jeweils ins Quadrat
- Zähle dann alle quadrierten Werte zusammen
- Teile anschließend durch n – 1 (oder durch n)
Um das Ganze an einem konkreten Beispiel zu veranschaulichen, nehmen wir eine Studie zum Selbstvertrauen bei Speed Dating Events, erhoben bei Erwachsenen über 18 Jahren. Das Selbstvertrauen wird zwischen 0 (gar nix vorhanden) und 30 (ergeht sich gern in Unwiderstehlichkeitsfantasien) skaliert. Hier sind die Daten:
1, 20, 26, 14, 9, 6, 19, 22 n = 8
Der Mittelwert ist 14.63 (hier musst du für die Berechnung im Gegensatz zum Median nicht nach Größe ordnen!). Ersteren setzen wir nun ganz gepflegt in die Formel ein.
Hier ist zunächst die Variante mit "geteilt durch n – 1":
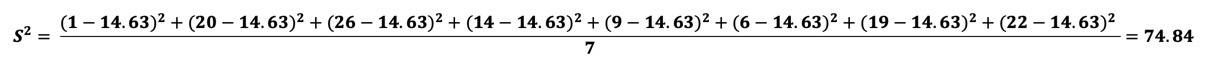
Die Varianz = 74.84 (ziemlich groß für diesen kleinen Datensatz und definitiv nicht interpretationstauglich).
Und nun die Version mit "geteilt durch n":
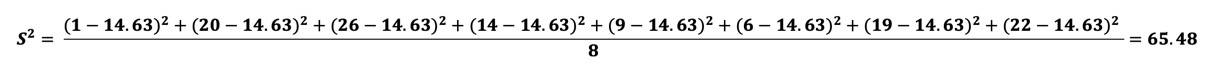
Die Varianz = 65.48 (auch nicht viel hilfreicher...).
Wie du siehst, bringt uns das bei einer Skala von 0 – 30 für die Interpretation nicht wirklich weiter... Daher schreiten wir nun gleich zur Standardabweichung.

brauchst du hilfe beim lernen von statistik?
Dann komm' zu statistik-gym, dem Online-Fitnessstudio für Statistik,
das dich fit für die Prüfung macht!
Eine Mitgliedschaft wie bei Netflix oder Spotify, nur eben für Statistik im Bachelor,
die dir hilft, dieses Fach endlich zu verstehen & die Prüfung zu meistern!
Darin bekommst du:
Und dann macht Statistik vielleicht sogar Spaß!
Klingt gut? Dann klick' hier:
Berechnung Standardabweichung
Wenn du die Varianz berechnet hast, ist der Löwenanteil bereits erledigt. Nun gilt es nur noch, die Wurzel aus der Varianz zu ziehen:
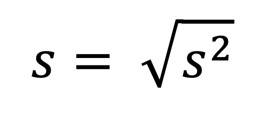
So gehst du vor:
- Berechne die Varianz
- Ziehe die Wurzel daraus
Bei unserem Beispiel zum Selbstvertrauen bei Speed Dating Events kommt Folgendes heraus – oben geteilt durch n - 1, unten durch n:
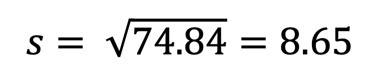

Und was sagt uns das jetzt?
Bezogen auf eine relativ überschaubare Skala von 0 bis 30 sind diese Werte ziemlich hoch, d. h. die Versuchspersonen unterschieden sich ziemlich in ihrem Selbstvertrauen. Man kann also nicht wirklich von einer homogenen Stichprobe sprechen.
Zusammengefasst:
Durchschnittlich hatten die Versuchs-Teilnehmer*innen einen Selbstvertrauenswert von ca. 15 (14.63), lagen also genau in der Mitte der Skala. Und typischerweise lagen die Werte zwischen 7 und 23 – ich runde hier und nehme für diese Aussage eine Standardabweichung von 8 um den Mittelwert herum, also 15 +/– 8 = 7 bzw. 23.
Hinter die Löffelchen schreiben:
Worauf du bei der Interpretation immer achten solltest, ist die Skala, auf der das interessierende Merkmal erhoben wurde. Es gilt also immer, die Größe der Standardabweichung ins Verhältnis zur Spannweite der Skala zu setzen.
Eine Standardabweichung von 2.2 ist bei einer Skala von 0 – 5 ziemlich hoch – und wäre bei einer Skala von 1 – 100 hingegen sehr gering.
Standardabweichung & Varianz mit SPSS
Beide Kennwerte lassen sich nicht exklusiv aufrufen, sondern werden bei verschiedenen Varianten der deskriptiven Statistiken mitgeliefert. Und wie so häufig bei SPSS, führen mehrere Wege zum Glück.
Geh' entweder auf "Analysieren", "Deskriptive Statistiken", "Häufigkeiten", dann auf den Button "Statistiken" und kreuz' beide Streuungsmaße an.
Oder du wählst den Weg über "Analysieren", "Deskriptive Statistiken", "Deskriptive Statistik". Hier wird die Standardabweichung bereits standardmäßig mit ausgeworfen. Wenn dich jedoch auch die Varianz interessiert, musst du im Eingabefenster für die Variablen bei "Optionen" einen Haken setzen.
Die umfassendste Auswertung erhältst du, wenn du auf "Analysieren", "Deskriptive Statistiken", "Explorative Datenanalyse" gehst. Ein Beispiel dafür findest du hier.
Zum Abschluss noch ein kleiner Steckbrief:
Steckbrief Standardabweichung & Varianz
Wie wär's mit einem virtuellen Fleißbild?
Na, wie sieht's aus – reicht die Motivation noch für eine unmittelbare Anwendung des Gelesenen?
Dann schnapp' dir einen kleinen Datensatz und rechne wild drauflos – und du erhältst ein virtuelles Fleißbild von mir.
Und nicht vergessen: Regelmäßig Belohnen!
Der Spaßfaktor von Statistik hält sich meist in eng umschriebenen Grenzen. Daher sollte man sich's beim und nach dem Lernen ganz arg gut gehen lassen. Zum Beispiel so:

QUELLEN (Als Amazon-Partnerin verdiene ich an qualifizierten Verkäufen):
Bortz, J., & Schuster, C. (2017). Statistik für Human- und Sozialwissenschaftler. Berlin: Springer.
KENNST DU SCHON MEINEN YOUTUBE-KANAL?

Guckst du hier:


Hallo liebe Frau Paul!
Bei der verzweifelten Suche nach Hilfe über Statistik bin ich auf Ihrer Seite gelandet und so sehr dankbar für Ihre Ausführungen. Endlich verstehe ich die Grundlagen und kann weiter darauf aufbauen. Ich wollte mein Studium schon abbrechen, weil mich die Angst vor Statistik so getrieben hat. DANKE!!!
Liebe Claudia,
das freut mich sehr!!!
Alles Gute für Ihr weiteres Studium und herzliche Grüße,
Melanie