Liebst du (B-/C-) Promi Celebrity-Shows wie z. B. Dschungelcamp? Ja? Und falls du dich auch schon einmal gefragt haben solltest, ob es bei den gruseligen Dingen, die alle Kandidat*innen dort essen müssen, unterschiedlich lange dauert, bis ein Brechreiz eintritt, solltest du unbedingt weiterlesen – denn im Folgenden weihe ich dich in die statistische Auswertung zu Fragestellungen dieser Art ein: die Varianzanalyse mit Messwiederholung (oder auch: Repeated Measures ANOVA).
Was ist die ANOVA mit Messwiederholung?
Im Gegensatz zur "regulären" Varianzanalyse (= Analysis of Variance, ANOVA) werden bei der ANOVA mit Messwiederholung bei denselben Personen wiederholte Messungen durchgeführt. Beispiele sind Fragestellungen wie:
- Verändert sich die Begeisterung für Statistik (sofern sie jemals vorhanden war) im Verlauf des Studiums? Messung zu Beginn des Studiums, kurz vor der ersten Prüfung und während des Verfassens der Bachelorarbeit.
- Schwankt die Konzentrationsfähigkeit im Tagesverlauf? Messung morgens, mittags und abends.
- Verändert sich die Lebensqualität bei Depressions-Patienten durch Kognitive Verhaltenstherapie? Messungen beispielsweise vor Aufnahme der Therapie, nach 5 sowie 10 Sitzungen und nach Abschluss der Therapie.
Das Prinzip ist also, dass bei denselben Personen die gleiche metrische abhängige Variable (AV) mehrmals unter verschiedenen Bedingungen gemessen wird (mindestens dreimal).
Diese Bedingungen (Faktoren) können Messzeitpunkte sein – oder aber, wie eingangs beschrieben, z. B. verschiedene Tiere, die jeweils von allen verspeist werden müssen (das sehen wir uns gleich mit SPSS an). Die unabhängige Variable (UV) bzw. der Faktor ist dabei diskret / kategorial, die AV stetig / metrisch.
Die ANOVA mit Messwiederholung stellt somit eine Erweiterung des t-Tests für abhängige Stichproben dar: Beim t-Test können immer nur zwei Mittelwerte bzw. Messzeitpunkte miteinander verglichen werden – will man nun aber mindestens drei Mittelwerte, die an denselben Personen erhoben wurden, miteinander vergleichen, so ist die Varianzanalyse mit Messwiederholung die Methode der Wahl.
Dieses Verfahren ist rechnerisch deutlich komplexer als die ein- und zweifaktorielle Varianzanalyse. Das Ziel dieses Artikels ist KEINE vollumfassende Erklärung der ANOVA mit Messwiederholung, sondern einzig und allein das Aufrufen und Interpretieren bei SPSS.
Damit du im Folgenden alles selbst nachvollziehen kannst, schreibe ich dir die einzelnen Schritte dazu, um die abgebildeten Ergebnistabellen zu erhalten.
Dabei gehe ich davon aus, dass du statistisches Vorwissen hast und dich mit der grundsätzlichen Bedienung von SPSS auskennst. Natürlich kannst du dir alles auch nur so durchlesen, ohne die Daten selbst aufzurufen.
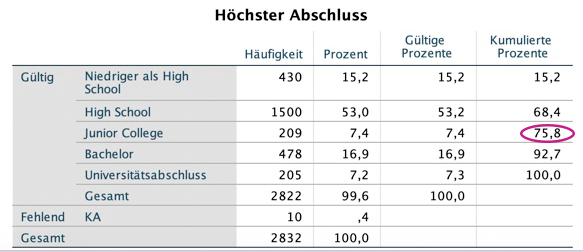
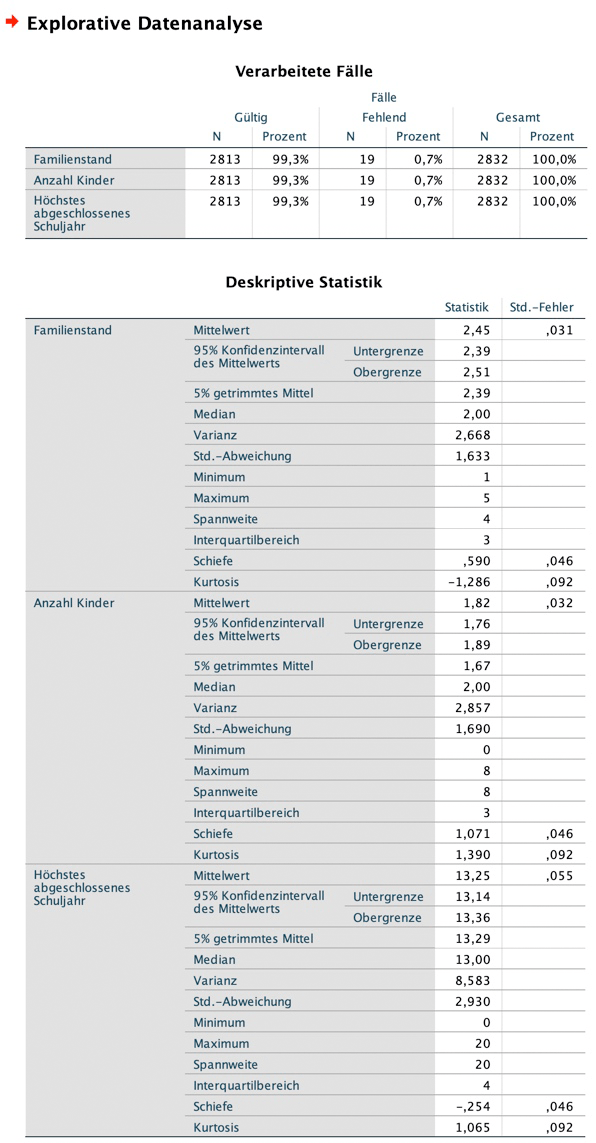
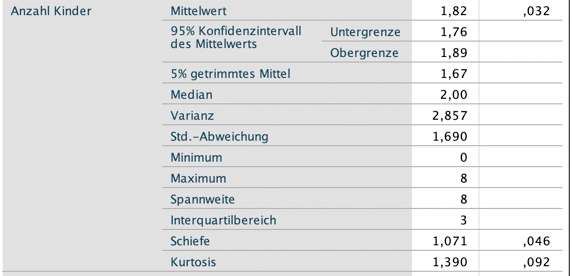
Hast du was anderes gesucht? Klick' hier für SPSS für die deskriptive Statistik, hier für Zusammenhangsmaße, hier für t-Test und Regression sowie hier für die ein- und zweifaktorielle Varianzanalyse.
Wo du Datensätze herbekommmst
Datensätze bekommst du auf verschiedensten Seiten im Internet sowie direkt im Programm SPSS. Ich empfehle z. B. die Datensätze von Andy Field, die hier zu finden sind.
Praktischerweise liefert SPSS aber auch eine Fülle von Datensätzen mit, die du folgendermaßen erreichen kannst:
Windows: C:/Programme/IBM/SPSS/Statistics/27 (oder eine andere Version)/Samples/German
Mac: Im Finder: Applications oder Programme/IBM/SPSS/Statistics/27 (oder eine andere Version)/Samples/German
SETTING: DSCHUNGELCAMP
Das fiktive Setting, das ich dem exzellenten Lehrbuch von Andy Field, Discovering Statistics using IBM SPSS Statistics, entnommen habe, ist Folgendes:
In einem Dschungelcamp müssen alle Teilnehmenden jeweils vier verschiedene (eher eklige) Tiere zu sich nehmen (diskreter Faktor / UV = Tier). Gemessen wird dann die Zeit, bis nach Genuss jedes Tiers ein Brechreiz auftritt (stetige AV).
Die Frage ist somit, welches Tier am ekelerregendsten ist bzw. ob sich die Zeiten bis zum Würgereiz abhängig vom Tier voneinander unterscheiden.
Der Faktor Tiere unterteilt sich in: Stabheuschrecke, Känguru-Hoden, Fischaugen sowie Witchetty-Maden (wie – die kennst du nicht???) und wird bei jeder Person gemessen. Alle Teilnehmenden essen also diese vier Tiere bzw. Tierteile (der Traum aller Veganer*innen – ich esse überwiegend vegan, habe also tiefstes Mitgefühl mit den Proband*innen).
Den dazugehörigen Datensatz findest du hier (gehe bitte auf "Andy Field's Datasets"). Die Datei, die wir brauchen, heißt bushtucker.sav.
Der Begriff Bush Tucker bezeichnet die ursprüngliche Ernährungsweise der Aborigines in Australien, mit allen erdenklichen Pflanzen und vor allem Tieren, die dort so kreuchen und fleuchen und zudem genießbar sind. Also eher nichts für schwache Nerven und empfindliche Gaumen.
ANOVA mit Messwiederholung mit SPSS
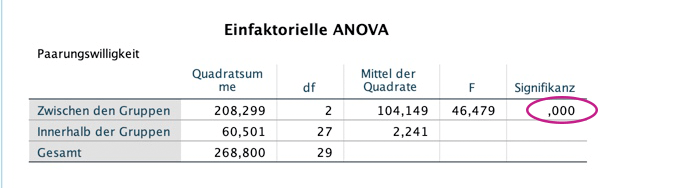
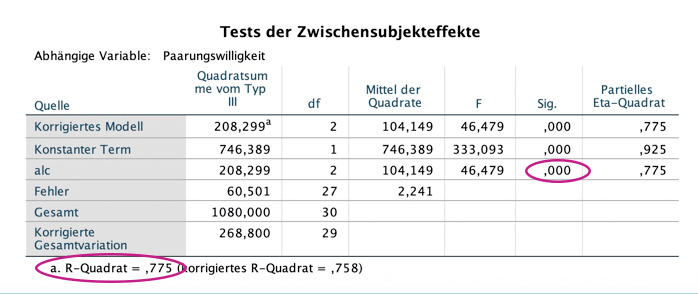
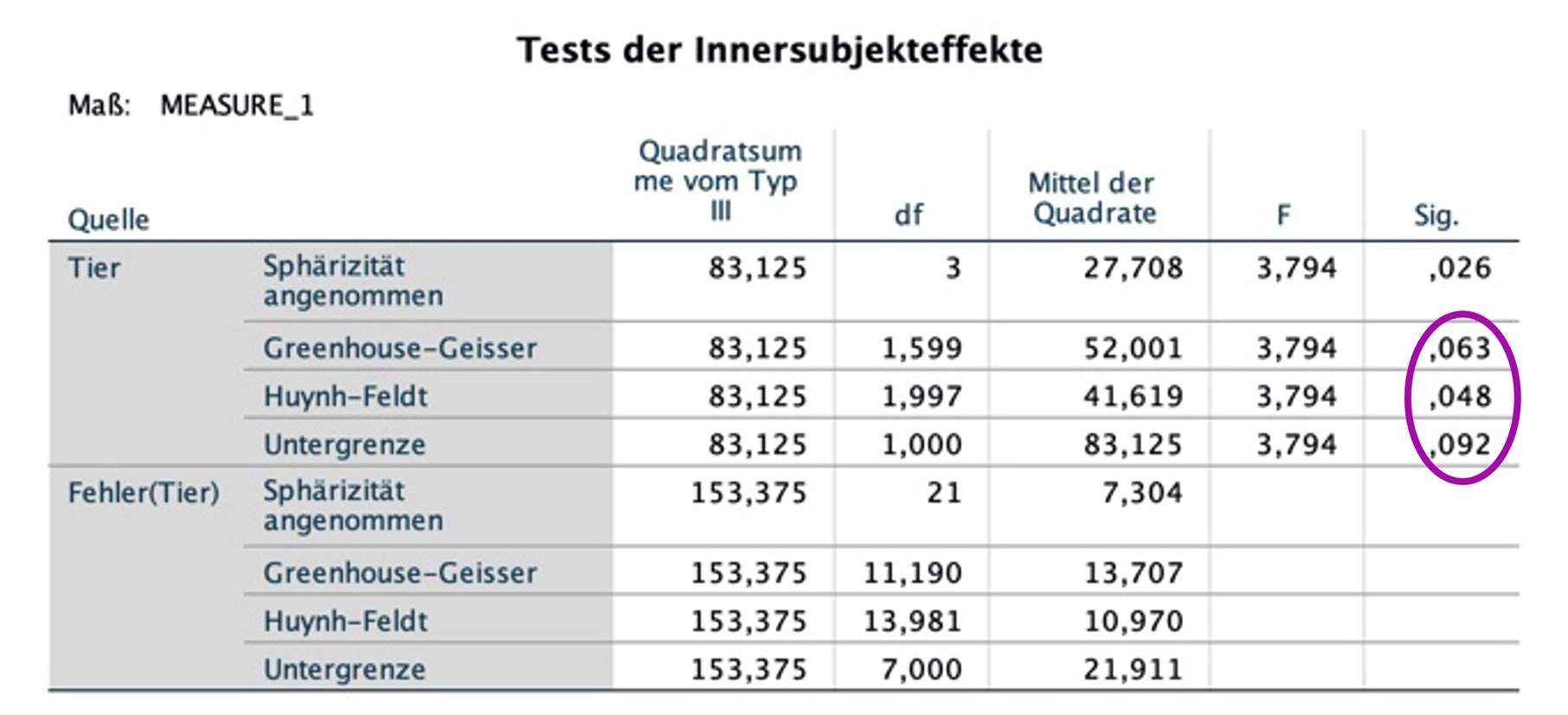
Die ANOVA mit Messwiederholung untersucht, ob sich die Mittelwerte der einzelnen Messzeitpunkte oder Faktorstufen signifikant voneinander unterscheiden.
Der dazugehöfige F-Test prüft die Nullhypothese, dass alle Mittelwerte gleich sind, es also keinen Unterschied in der AV gibt und somit keine Faktorstufe irgendeinen Einfluss auf die AV hat.
Dieser Test wird auch "Globaler F-Test" oder "Omnibus-Test" genannt. "Global" deshalb, weil ein signifikantes Ergebnis nur aussagt, dass sich mindestens zwei Mittelwerte voneinander unterscheiden – welche das sind, erfährt man jedoch nicht.
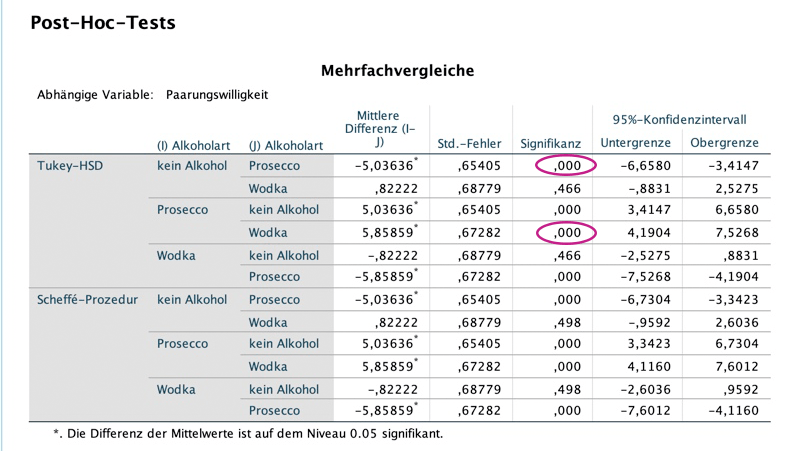
Daher dient die Varianzanalyse mit Messwiederholung als Basis für weitere Verfahren wie Post-hoc Tests, mit deren Hilfe die genauen Mittelwerts-Unterschiede untersucht werden können. Zudem kann man sich natürlich auch die deskriptiven Statistiken sowie Grafiken betrachten, um zu sehen, welche Mittelwerte sich in welcher Richtung voneinander unterscheiden. Wir machen im Folgenden beides.
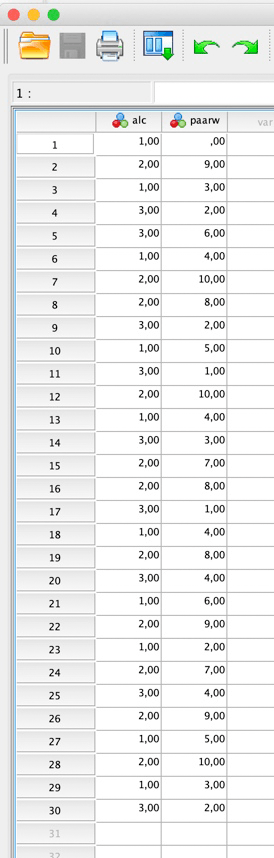
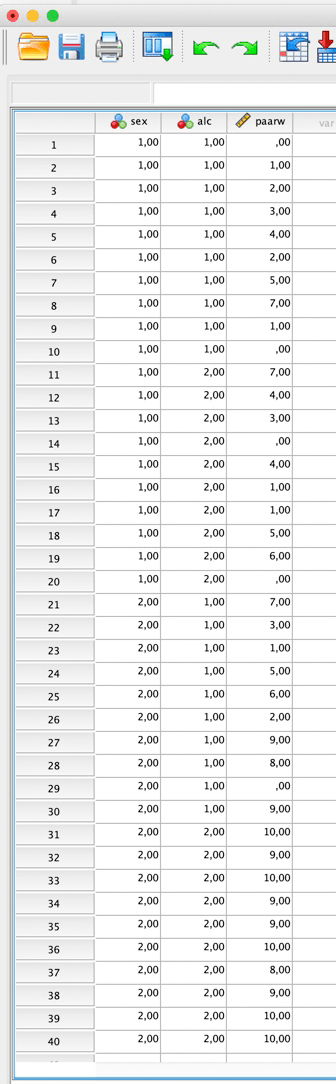
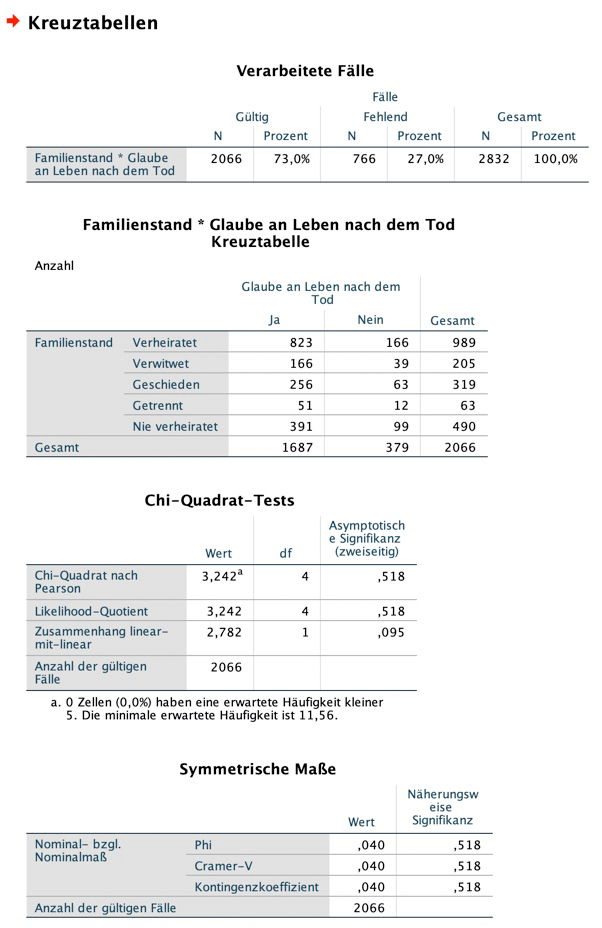
Zunächst siehst du hier die Datenansicht. Wir haben sagenhafte 8 Versuchspersonen (Celebrities) und bei jeder wurde die Dauer in Sekunden gemessen, bis der Würgereiz auftrat:
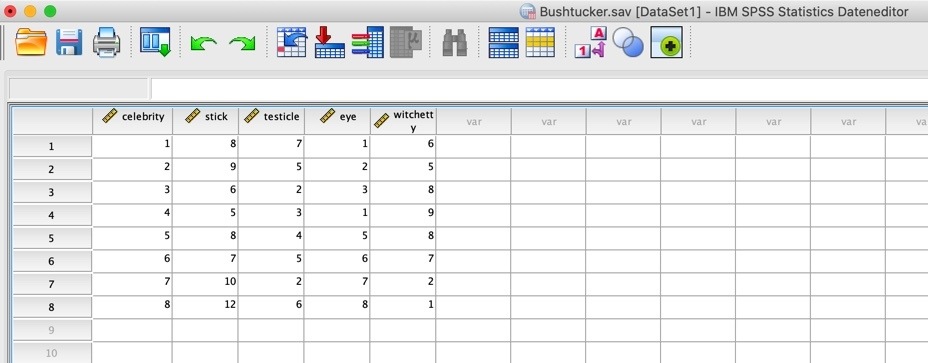
Um nun die ANOVA mit Messwiederholung aufzurufen, gehe auf "Analysieren", "Allgemeines lineares Modell", "Messwiederholung". Im sich öffnenden Fenster ersetzt du "Name des Innersubjektfaktors" mit "Tier" und gibst bei "Anzahl der Stufen" 4 ein (wir haben vier leckere Tiere bzw. Teile von Tieren).
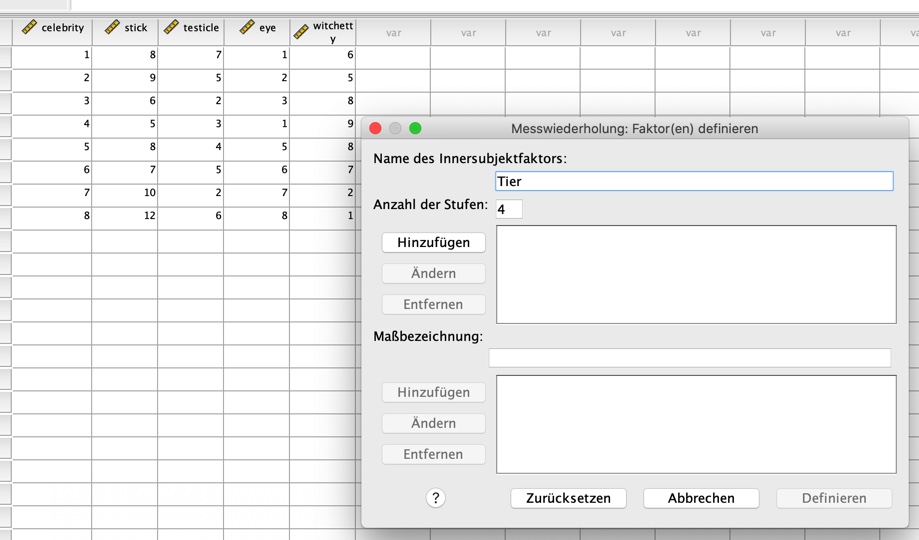
Dann klickst du links unter "Anzahl der Stufen" auf "Hinzufügen" und danach auf "Definieren". Jetzt öffnet sich folgendes Fenster, wo du dann die einzelnen Faktorstufen (hier: Tiere) den Messungen bzw. "Innersubjektvariablen" zuordnen musst. Du musst also definieren, was Messung 1, 2, 3, und 4 sein soll.
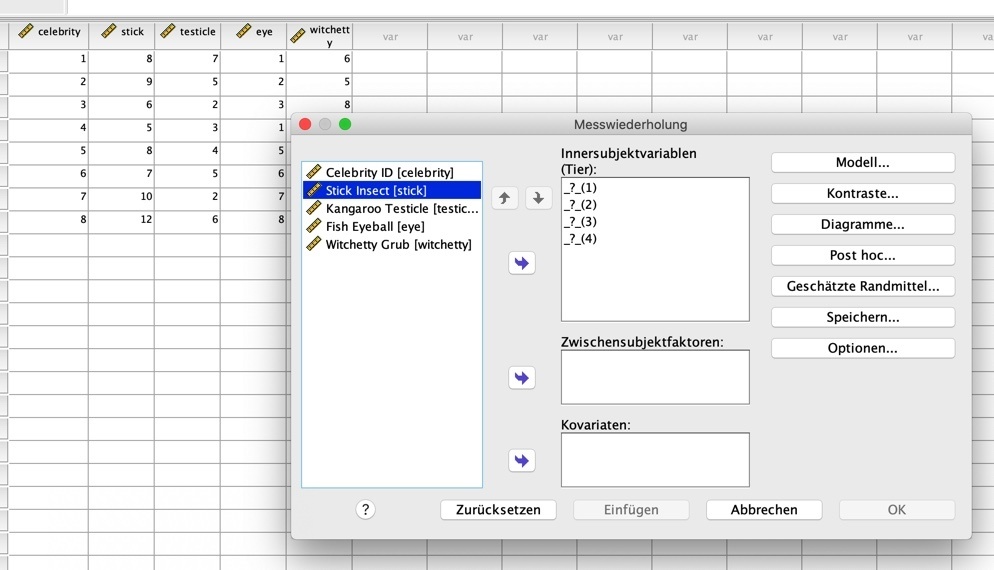
Dies machst du, indem du die jeweiligen Variablen links anklickst, so dass sie blau erscheinen, und dann auf den blauen Pfeil klickst, der sie in das rechte Feld "Innersubjektvariablen" verschiebt. Das sieht dann so aus:
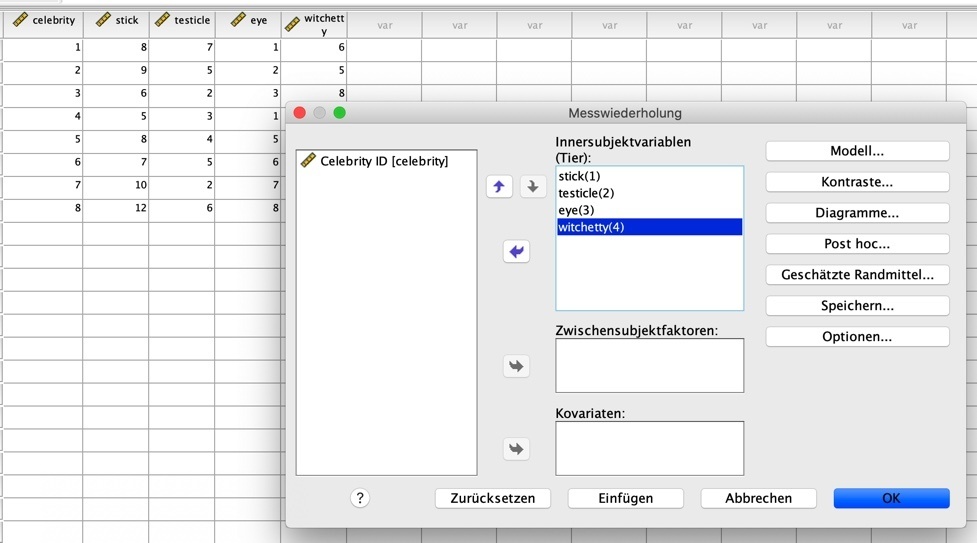
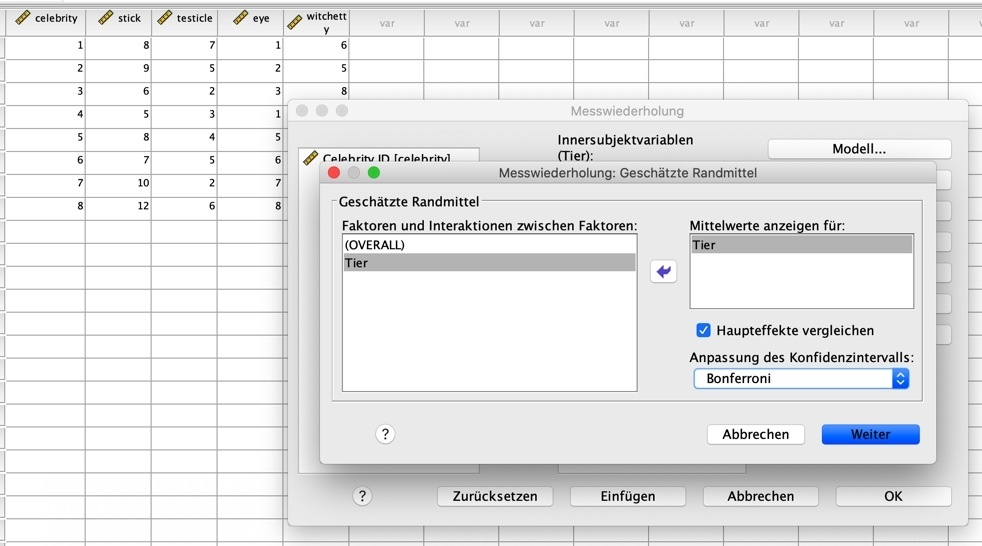
Um die Post-hoc Tests aufzurufen, muss man nun etwas komplizierter vorgehen und tapfer auf "Geschätzte Randmittel" klicken (Post-hoc Tests überprüfen, welche Mittelwerte sich jeweils voneinander unterscheiden).
Hier klickst du unseren Faktor "Tier" an und verschiebst ihn in das Feld "Mittelwerte anzeigen für:". Setz' bitte zudem einen Haken bei "Haupteffekte vergleichen" und wähle in dem Drop-down Menü "Bonferroni" aus.
Das Fenster sollte dann so aussehen:
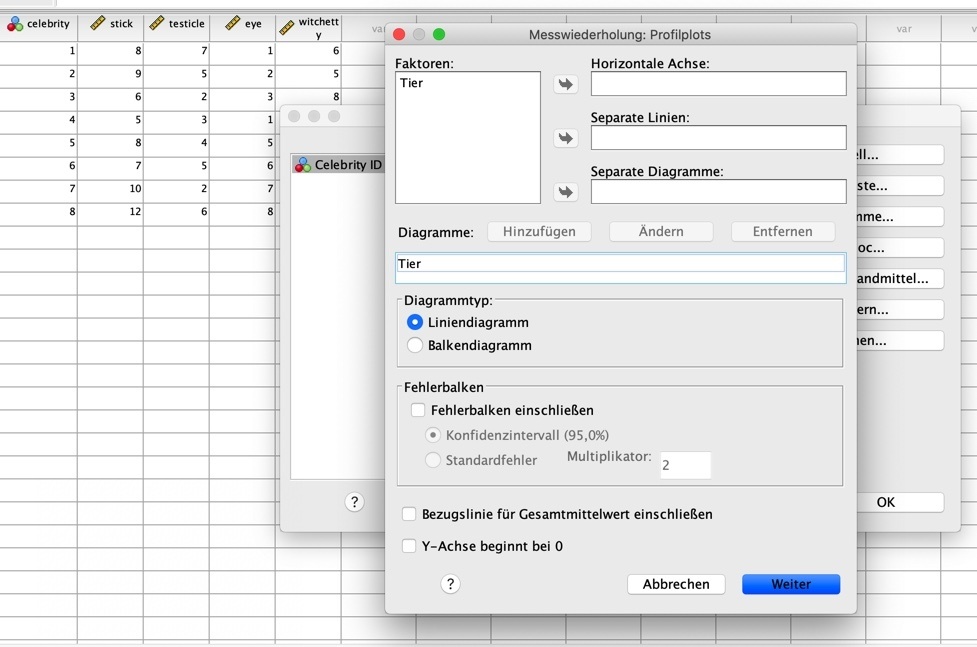
Dann klickst du auf "Weiter" und kommst zum vorherigen Fenster. Unter "Optionen" fordern wir uns noch die "Deskriptiven Statistiken" an (kein Bild dazu, das bekommst du so hin).
Bei "Diagramme" verschiebst du den Faktor "Tier" in das Feld "Horizontale Achse", klickst auf "Hinzufügen", bestätigst mit "Weiter" und schließt mit OK ab.
SPSS rechnet sich jetzt den Wolf und nun siehst du ganz viele schöne bunte Zahlen und Tabellen.
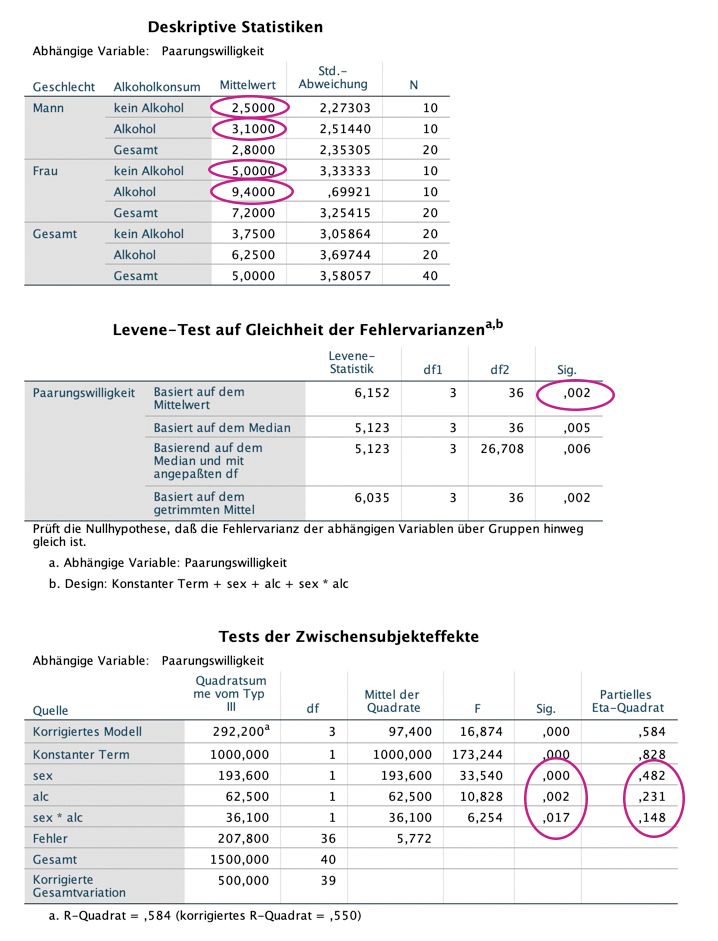
Betrachten wir zunächst die deskriptiven Statistiken:

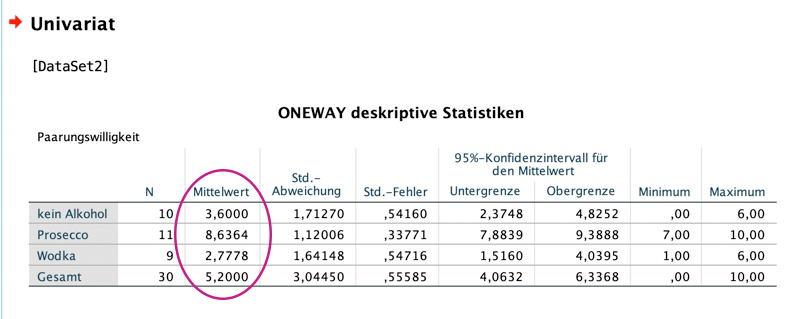
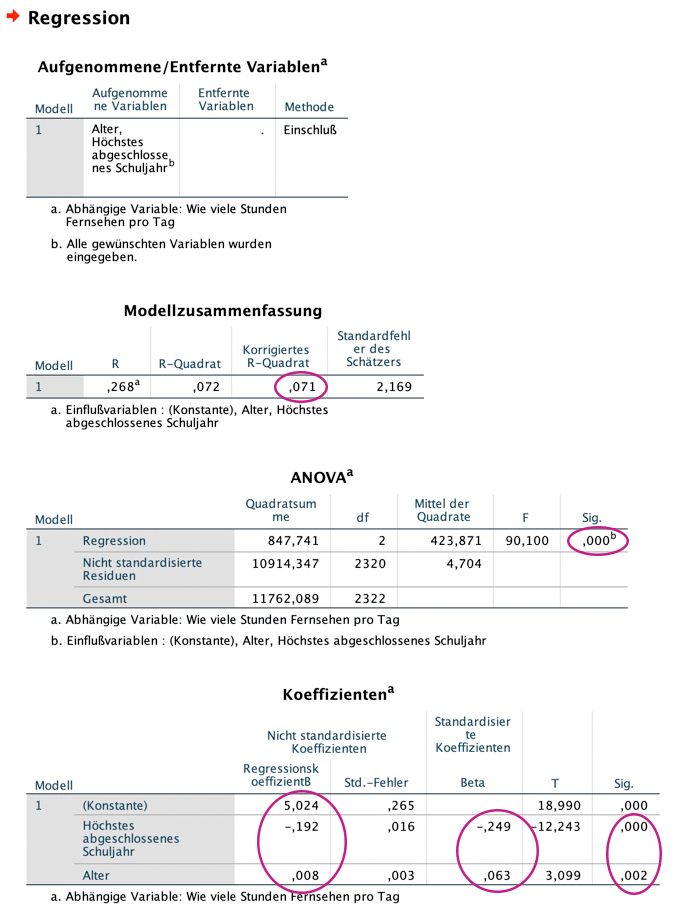
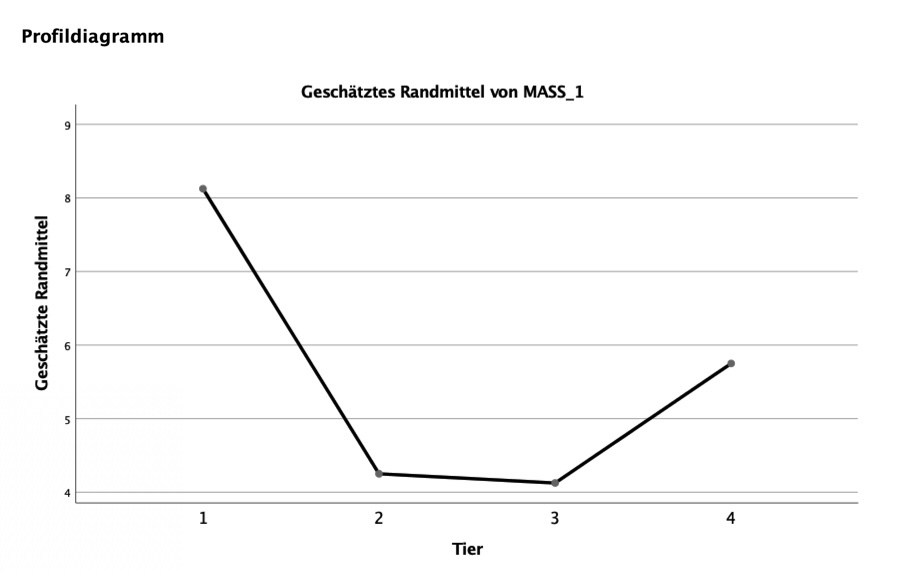
Aus den Mittelwerten lässt sich erkennen, dass die Fischaugen die Spitzenreiter sind, was das schnelle Auslösen eines Brechreizes anbelangt: hier dauert es nur 4.13 Sekunden, dicht gefolgt von den Känguru-Hoden (4.25 sec). Ich hätte eher auf die Maden getippt.
Im Gegensatz dazu scheint die Stabheuschrecke nahezu eine Delikatesse zu sein, denn da brauchen die Celebrities immerhin 8.13 Sekunden, bis der Würgereiz einsetzt.
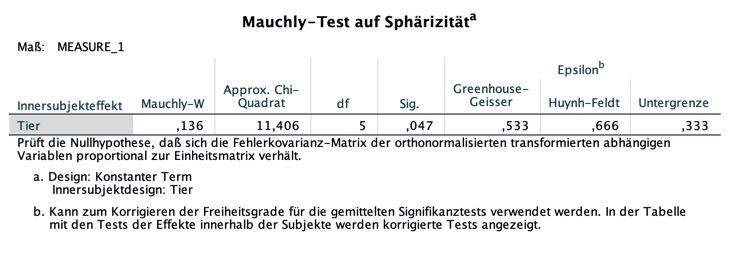
Als nächstes sehen wir uns den Mauchly-Test an, der meinen absoluten Lieblingssatz in der gesamten Statistik enthält. Dieser lautet folgendermaßen:
Prüft die Nullhypothese, dass sich die Fehlerkovarianz-Matrix der orthonormalisierten transformierten abhängigen Variablen proportional zur Einheitsmatrix verhält!
Da kannst mal sehen...
Der Mauchly-Test prüft eine der Voraussetzungen der Varianzanalyse mitt Messwiederholung, nämlich die Sphärizität. Sphärizität heißt, dass die Varianzen der Differenzen zwischen den einzelnen Messreihen der verschiedenen Faktorstufen gleich sind. Hä???
Bedeutet:
Man nimmt z. B. den Brechreiz-Dauer-Wert von Celebrity 1 bei Stabheuschrecke und zieht ihn vom Brechreiz-Dauer-Wert von Celebrity 1 bei Känguru-Hoden ab. Dies wird nun auch für die anderen 7 Teilnehmenden gemacht und dann wird aus diesen insgesamt 8 Differenzwerten eine Varianz errechnet.
Diese sollte nun ähnlich wie die Varianz der Differenzwerte zwischen Känguru-Hoden und Fischaugen, Fischaugen und Witchetty-Maden und so weiter sein. Die Varianzen aller möglichen paarweisen Kombinationen sollen gleich sein.
Der Mauchly-Test überprüft die Nullhypothese, dass dem so ist, dass also Sphärizität vorliegt.
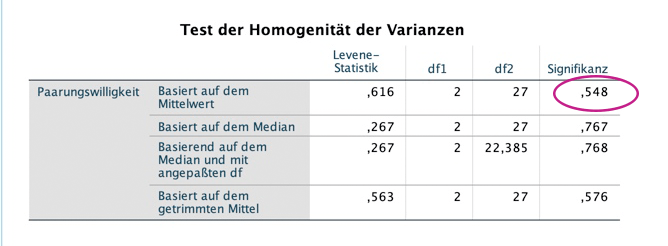
Wird er signifikant (p-Wert bei "Sig." kleiner 0.05), so ist diese Annahme verletzt. Allerdings ist das Ganze mit Vorsicht zu genießen, denn die Ergebnisse des Tests hängen stark von der Stichproben-Größe ab. Hier ist der Mauchly-Test signifikant: bei "Sig." steht ein p-Wert von .047.
Allerdings ignorieren wir diesen Test aus oben genanntem Grund und sehen uns bei den Ergebnissen, die jetzt im Anschluss folgen, lieber gleich die Zeilen an, wo mit Korrekturverfahren gerechnet wurde.
Die Korrekturverfahren werden angewendet, damit bei einer Verletzung der Sphärizität nicht zu schnell ein signifikantes Ergebnis erreicht wird, ohne dass ein Effekt vorliegt (das wäre dann ein Alpha-Fehler oder Fehler erster Art).
Nun zum "eigentlichen" Test der ANOVA mit Messwiederholung, dem F-Test:

Daher sehen wir uns jetzt die Einzelvergleiche der Mittelwerte mit den Post-hoc Tests an:

Geschafft, du Hecht*in!
Wenn du bis hierher tapfer durchgehalten hast, bekommst du ein wunderschönes, virtuelles und vor allem tierfreies, sprich: veganes Fleißbild von mir!
Meine Challenge an dich:
Schnapp' dir jetzt im Sinne von "Turning insight into action" einen anderen Datensatz und führ' doch gleich mal eine ANOVA mit Messwiederholung durch! Viel Erfolg und Spaß dabei!
KENNST DU SCHON MEINEN YOUTUBE-KANAL?

Guckst du hier:
Fühlst du dich lost im dschungel der Statistischen methoden?
Dann schnapp' dir das E-Book (0,-€):
endlich durchblick in statistik!
in 4 einfachen schritten zur wahl der richtigen methode