Median verständlich erklärt
Median oder Mittelwert – das ist hier die Frage! Wann nimmt man was? Und was ist der Median überhaupt? Wie wird er berechnet? Für die Eiligen gibt's zunächst die Kurzversion (quasi ein Spoiler, bevor's überhaupt mit dem Artikel losgeht...):
Der Median oder auch Zentralwert ist derjenige Wert, der in einer nach Größe geordneten Reihe von Werten genau in der Mitte liegt.
Stell' dir vor, du schreibst alle in einem Datensatz vorkommenden Werte nach Größe geordnet längs auf ein Blatt Papier, von Rand zu Rand. Anschließend faltest du das Papier genau in der Mitte: dann ist der Wert, der auf dem Knick liegt, der Median.
Was ist der Median?
Der Median unterteilt einen nach Größe geordneten Datensatz in zwei Hälften: mindestens 50% der Daten sind kleiner als (oder gleich) und mindestens 50% sind größer als (oder gleich) dem Median.
Es ist derjenige Wert, der genau in der Mitte des Datensatzes liegt – daher der Name "Zentralwert". Er ist ein Maß für die zentrale Tendenz.
Bei einem ungeraden Datensatz ist der Zentralwert direkt im Datensatz enthalten, bei einem ungeraden Datensatz wird er aus den beiden in der Mitte befindlichen Werten gemittelt, also sozusagen künstlich erschaffen.
Weitere alternative Bezeichnungen sind 2. Quartil (Q2) und das 50%-Quantil.
In welchen Bereich der Statistik gehört er?
Der Zentralwert gehört in die Welt der beschreibenden oder deskriptiven Statistik. Bei der Deskriptivstatistik geht's darum, die in einem Datensatz enthaltene Information auf wenige Kennwerte zu reduzieren und zudem grafisch darzustellen. Es werden im Gegensatz zur Inferenzstatistik keine Schlüsse auf die dazugehörige Grundgesamtheit gezogen, sondern nur beschrieben, was in einer bestimmten Stichprobe zu finden ist.
Der Median gehört zu den Lagemaßen, die den Schwerpunkt eines Datensatzes beschreiben.
Was sagt der Median aus?
Ehrlich gesagt lässt sich hier nicht so wahnsinnig viel hineininterpretieren. Nur dies: bis zu diesem Punkt haben sich 50% aller Werte angesammelt und 50% liegen darüber. That's it.
Wann nimmt man ihn her?
Wenn es Ausreißer oder Extremwerte im Datensatz gibt und der Mittelwert nicht verwendet werden sollte – oder wenn ordinalskalierte Daten vorliegen. Man verwendet den Median, um die Mitte eines Datensatzes bestimmen bzw. quantifizieren zu können.
Achtung: Bei ordinalskalierten Daten wie z. B. Rangplätzen und geradem Datensatz ist der Median nicht eindeutig festzulegen: Wenn es beispielsweise in einem Schönheitswettbewerb den 1., 2., 3. und 4. Platz gibt, läge der Median rechnerisch zwischen dem 2. und dem 3. Platz. Das wäre dann der 2.5te Platz, den es jedoch nicht gibt!
Median ohne Formeln
Die Berechnung des Zentralwerts ist recht einfach, wird jedoch wie üblich in der Statistik etwas kompliziert dargestellt. Wie du gleich sehen wirst, gibt es zwei Varianten: einmal für einen ungeraden und einmal für einen geraden Datensatz.
Als Beispiel nehmen wir eine Erhebung zur Angst, etwas zu verpassen (FOMO = Fear of Missing Out), erhoben bei Jugendlichen zwischen 14 und 18 Jahren. FOMO wird hier zwischen 0 (keinerlei Angst, tiefenentspannt) und 100 (Stirbt gefühlt, wenn nicht alle Social Media Feeds minütlich gecheckt werden) skaliert. Dies sind die Daten:
Ungerader Datensatz: 23, 56, 87, 30, 28, 45, 66, 18, 49, 48, 55 n = 11
Gerader Datensatz: 23, 56, 87, 30, 28, 45, 66, 18, 49, 48 n = 10
Ungerader Datensatz
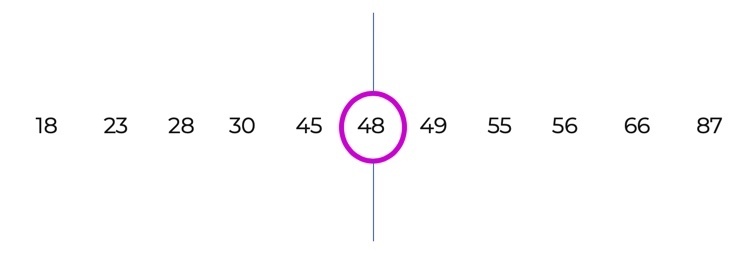
Auch ohne Formeln ist der erste Schritt immer, die Daten nach Größe zu ordnen!
Danach schaust du einfach, welcher Wert genau in der Mitte liegt: hier ist es die 48. Bingo.
gerader Datensatz
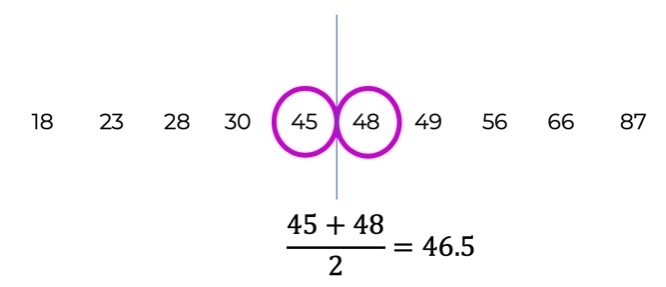
Hier musst du einfach nur die beiden in der Mitte stehenden Werte mitteln – et voilà!

brauchst du hilfe beim lernen von statistik?
Dann komm' zu Statistik-gym, dem Online-Fitnessstudio für Statistik,
das dich fit für die Prüfung macht!
Eine Mitgliedschaft wie bei Netflix oder Spotify, nur eben für Statistik im Bachelor,
die dir hilft, dieses Fach endlich zu verstehen & die Prüfung zu meistern!
Darin bekommst du:
Und dann macht Statistik vielleicht sogar Spaß!
Klingt gut? Dann klick' hier:
Berechnung des Medians mit Formeln
Und nun das Ganze mit Formeln für die beiden Varianten. Die tiefergestellten Klammern rechts neben den x zeigen Positionsnummern an, also an welcher Stelle ein bestimmter Wert in einer nach Größe geordneten Datenreihe steht.
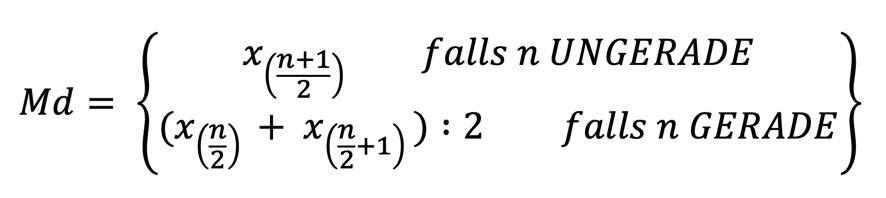
Berechnung bei ungeradem Datensatz
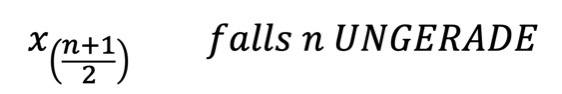
1. Ordne nach Größe

2. Rechne die Positionsangabe in der Klammer aus
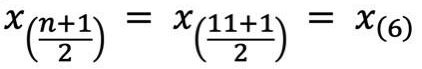
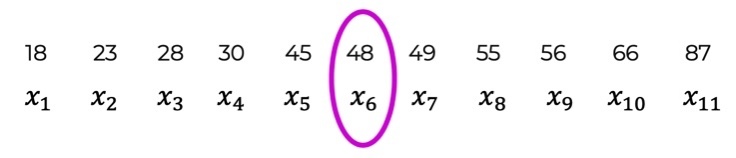
3. Welcher Wert befindet sich an dieser Position?
Das ist der Median!
Berechnung bei geradem Datensatz
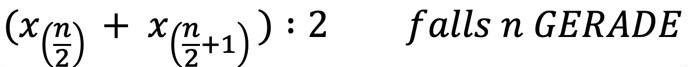
1. Ordne nach Größe

2. Rechne die Positionsangaben in den Klammern aus
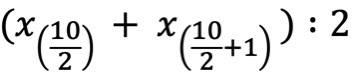
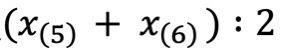
3. Welcher Werte befinden sich an diesen Positionen?
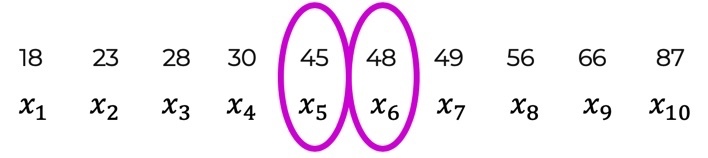
4. Setze diese Werte in die Formel ein und du bekommst den Wert des Medians
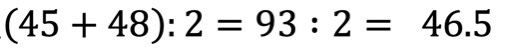
Zusammengefasst:
Bei ungeraden Stichproben rechnest du eine Position aus und schaust dann den Wert nach.
Bei geraden Stichproben wechselst du von der Positionsberechnung zum Rechnen mit „richtigen“ Werten und bekommst als Ergebnis gleich den Wert des Medians heraus (und nicht seine Position).
Median mit SPSS
Den Median kannst du nicht exklusiv aufrufen, sondern bekommst ihn bei der Explorativen Datenanalyse mitgeliefert.
Dazu gehst du auf "Analysieren", "Deskriptive Statistiken", "Explorative Datenanalyse". Im sich öffnenden Fenster wählst du die dich interessierenden Variablen aus, verschiebst sie in das Feld "Abhängige Variablen" und drückst auf "OK". Ein Beispiel dafür findest du hier.
Zu guter Letzt noch eine kleine Kurz-Übersicht:
Steckbrief Median
geschafft!
Turning insight into action…
Wie wär's – reicht die Motivation noch für eine unmittelbare Anwendung des Gelesenen? Dann könntest du zum Beispiel die oben angegebenen Werte bei SPSS eingeben und die Explorative Datenanalyse rechnen lassen.
Oder du überlegst dir eine fiktive Untersuchung nebst Zahlen und rechnest wild drauflos.
Variante 3: Such' dir Übungsaufgaben – entweder im Internet oder in deinen Lehr- bzw. Übungsbüchern.
Oder aber du machst nichts... auch gut.
Aber vorher gilt wie immer: Belohnen!
Statistik ist bekanntlich nicht so lustig. Daher sollte man sich's nach dem Lernen (oder auch währenddessen) unbedingt gut gehen lassen...

QUELLEN (Als Amazon-Partnerin verdiene ich an qualifizierten Verkäufen):
Bortz, J., & Schuster, C. (2017). Statistik für Human- und Sozialwissenschaftler. Berlin: Springer.
Field, A. (2018). Discovering Statistics using IBM SPSS Statistics. London: SAGE.
KENNST DU SCHON MEINEN YOUTUBE-KANAL?

Guckst du hier:

Gut
Dankeschön! Liebe Grüße
sehr hilfreich und verständlich erklärt
Dankeschön, freut mich sehr!