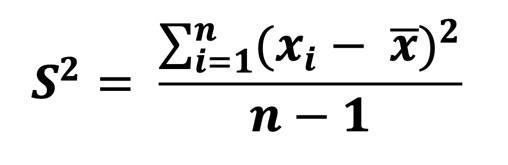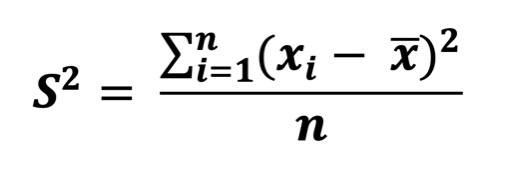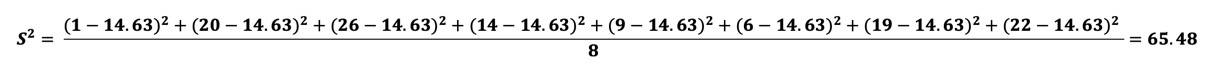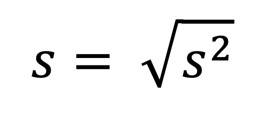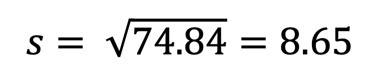Wer hätte es gedacht: selbst in der Statistik gibt es die sagenumwobene Glaskugel zur Prognose menschlichen Erlebens und Verhaltens – die lineare Regression! Kurz & knackig: wenn du einen linearen Zusammenhang zwischen zwei Variablen hast, kannst du mit der einen Variable die andere (mehr oder weniger gut) vorhersagen. Das Zauberwort heißt hier VORHERSAGE! Wenn du das irgendwo liest, geht es in in den allermeisten Fällen um die Regression.
Was ist die einfache lineare Regression?
= Statistische Methode zur Vorhersage bei vorab bestehendem linearen Zusammenhang zwischen zwei metrischen Variablen
BEISPIEL:
Angenommen, du stellst in einer Studie einen linearen Zusammenhang (siehe unten) zwischen Humor und Freudfähigkeit fest. Nun könntest du dir die Frage stellen, ob vielleicht das Ausmaß an Humor das Ausmaß an Freudfähigkeit vorhersagen könnte.
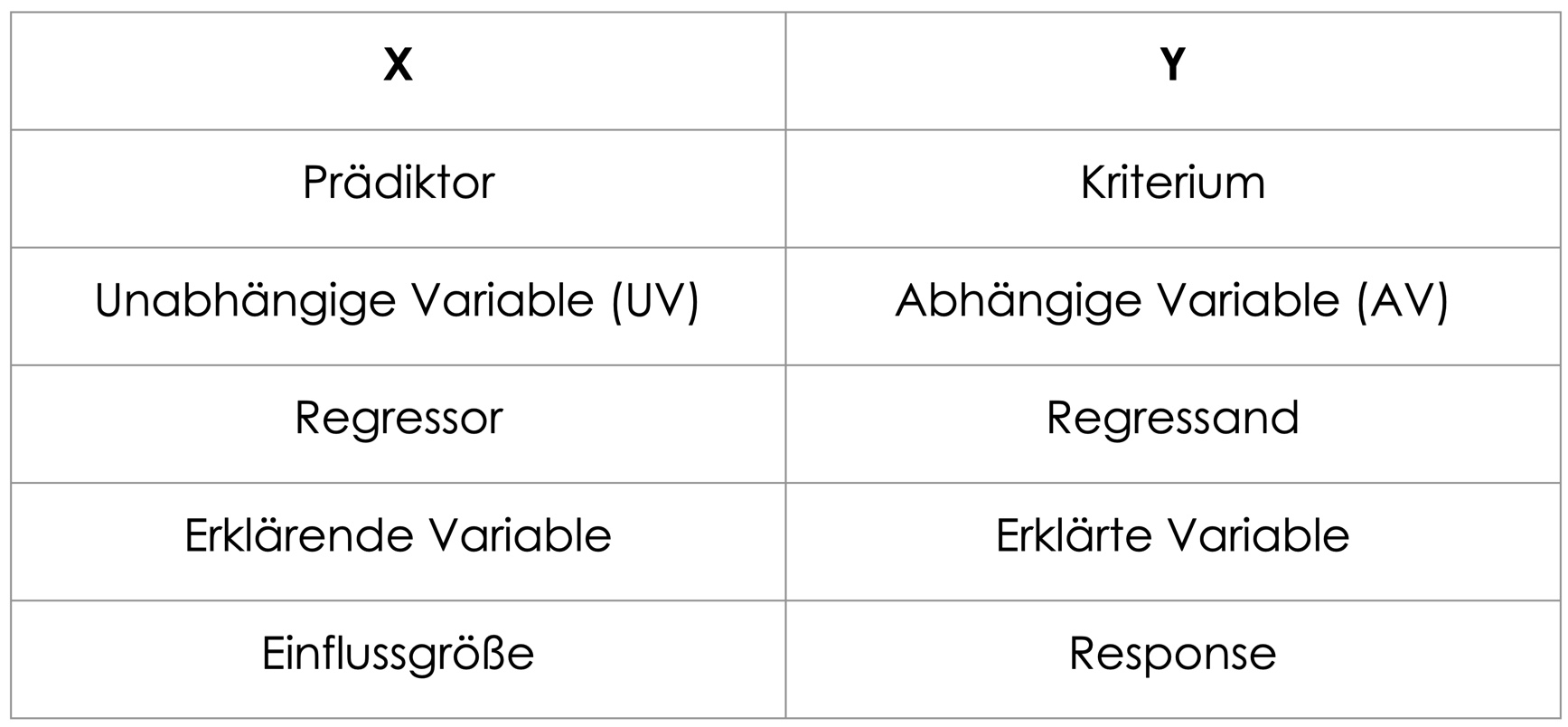
Du schnappst dir eine der beiden Variablen, z. B. den Humor, und machst sie zur vorhersagenden Variable (= Prädiktor) und die andere deklarierst du als die vorherzusagende Variable (= Kriterium).
Als Ergebnis erhältst du dann ein Modell (= eine Gleichung – mehr dazu weiter unten), mithilfe dessen du für jeden beliebigen Wert an Humor den entsprechenden Freudfähigkeits-Wert vorhersagen kannst.
Quasi im Sinne von: sag' mir dein Ausmaß an Humor – und ich sage dir, wie freudfähig du vermutlich bist!
Die einzelnen Bestandteile in "einfache lineare Regression":
EINFACHE: EINE metrische Variable (= Merkmal) sagt eine andere vorher
LINEARE: zwischen den beiden Variablen muss ein LINEARER ZUSAMMENHANG bestehen. Das ist ein Zusammenhang, der durch eine Gerade darstellbar ist und nicht z. B. U-förmig oder umgekehrt U-förmig aussieht, denn bei kurvilinearen Zusammenhängen funktioniert dieses Verfahren nicht!
Für die Berechnung einer linearen Regression brauchen wir also Zusammenhänge, die so aussehen:
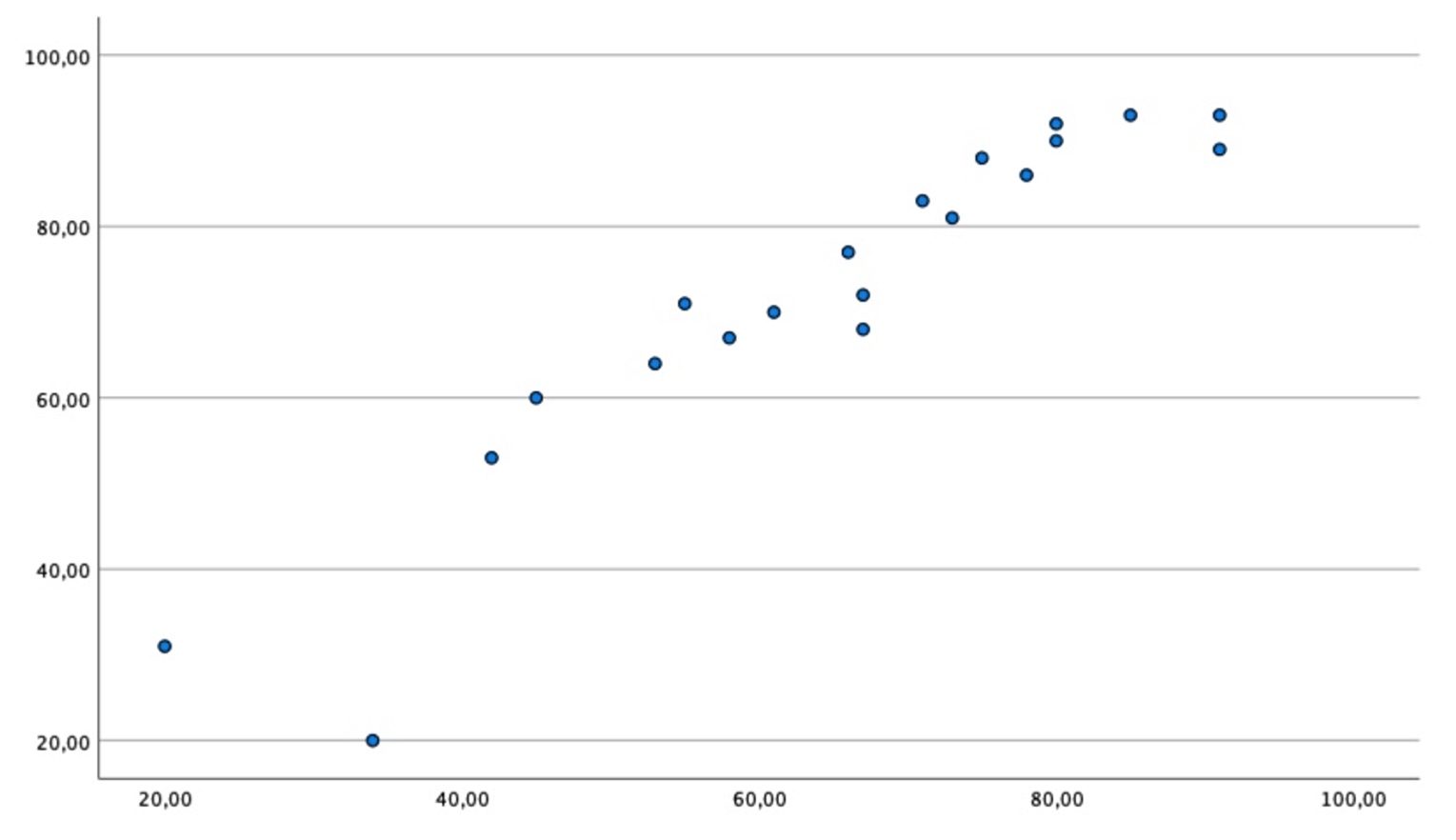
- mehr oder weniger geordnete Punktewolke, die von links unten nach rechts oben geht = positiver Zusammenhang
ODER
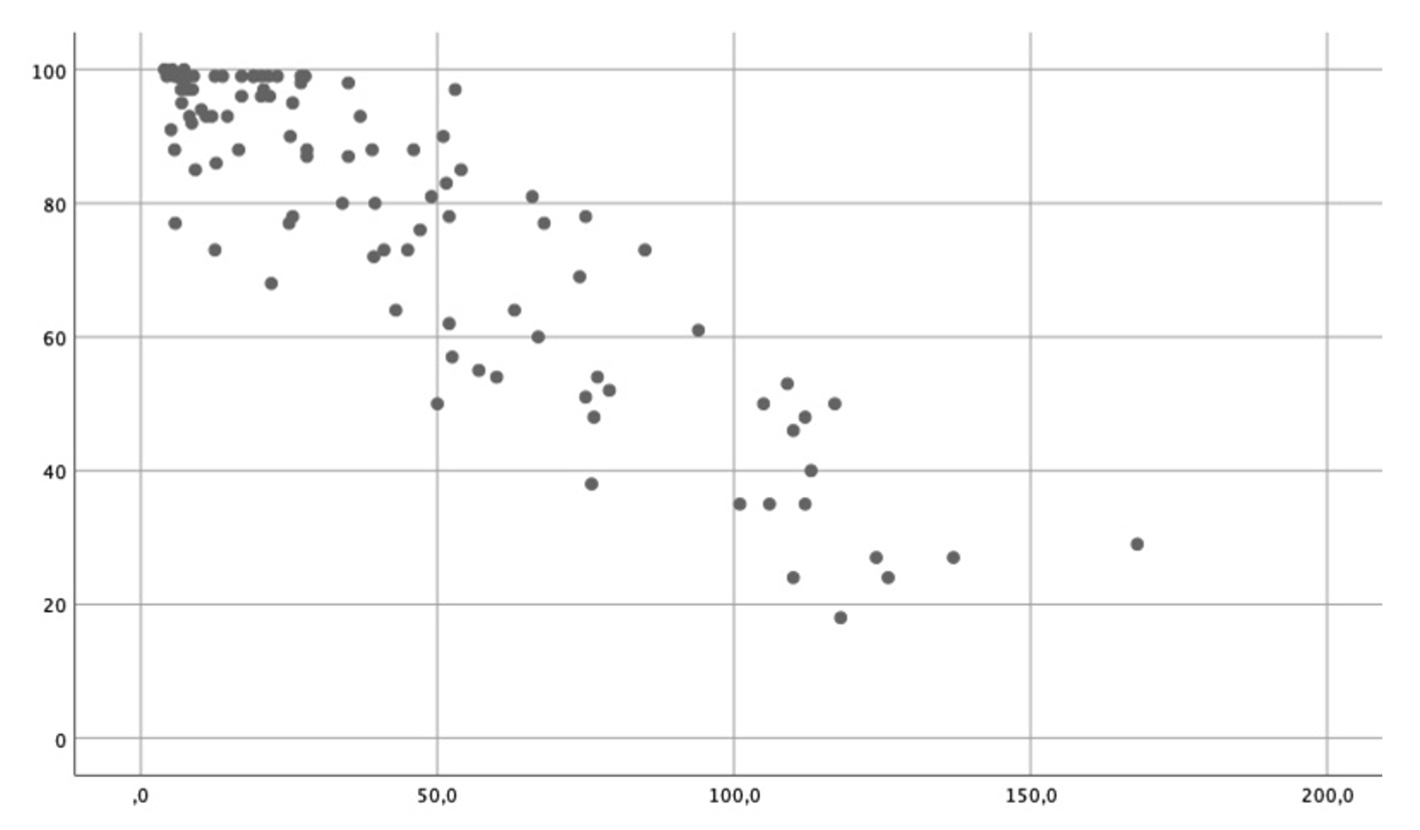
- mehr oder weniger geordnete Punktewolke, die von links oben nach rechts unten geht = negativer Zusammenhang
Guckst du hier für Beispiele: 1. Bild: positiver, 2. Bild: negativer linearer Zusammenhang
REGRESSION: kommt aus dem Lateinischen "regredi": zurückkehren, zurückkommen. Die Ausprägung der einen Variable wird auf die andere zurückgeführt.
ZIEL DER einfachen linearen REGRESSION:
Ein Modell zu erhalten, mit dem man für jeden beliebigen Wert der einen Variablen den dazugehörigen Wert der anderen vorhersagen kann!
Hinter die Löffelchen schreiben:
Bei der Regression darf man NICHT von einem kausalen Zusammenhang sprechen!
Auch wenn die Interpretation oft so klingt.
Die Vorhersage ist stochastisch, d. h. vom Zufall abhängig, und NICHT deterministisch!
Deterministisch wäre eine Aussage wie: IMMER wenn jemand einer Humor-Wert von 56 hat, wird sie / er einen Freudfähigkeits-Wert von 63 haben.
In welchen Bereich der Statistik gehört sie?
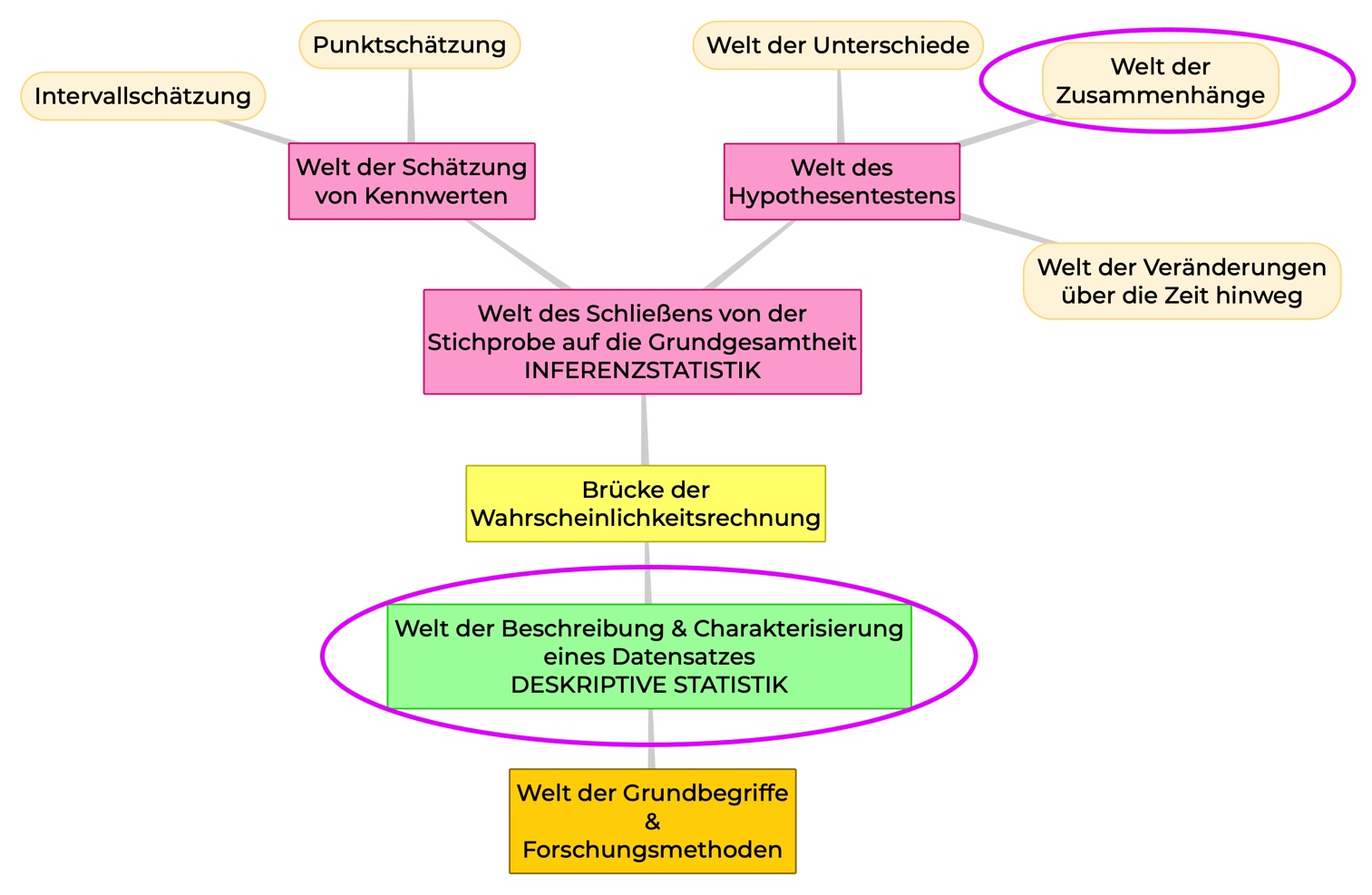
Deskriptive Statistik (Zusammenhänge):
Wenn die Regression rein beschreibend eingesetzt wird und NICHT auf die dazugehörige Grundgesamtheit verallgemeinert werden soll, gehört sie zur deskriptiven bzw. beschreibenden Statistik.
ODER:
Inferenzstatistik – Welt der Zusammenhänge:
Wenn die Regression dafür eingesetzt wird, um auf die dazugehörige Grundgesamtheit (= Population) zu schließen, zählt man sie zur schließenden oder Inferenzstatistik.
In diesem Blog Post wird nur die beschreibende Variante behandelt!
Die inferenzstatistische Auswertung mit SPSS findest du hier.
Typische Fragestellungen
Lässt sich das Einkommen aus dem IQ vorhersagen?
Sagt das Ausmaß an Vorbereitungszeit den Klausurerfolg voraus?
Kann man mit der Anzahl an konsumierten Zigaretten die Lebensdauer vorhersagen?
Ist die Hochsensibilität ein Prädiktor für Empathie?
Voraussetzungen
Linearer Zusammenhang zwischen den beiden Variablen
y : mindestens intervallskaliert & normalverteilt
Werte der Versuchspersonen sind unabhängig voneinander
Normalverteilte Fehler
Homoskedastizität: die Residuen (siehe unten) sollen alle ähnlich um die Regressionsgerade streuen
Vorgehen Regression in a nutshell
Nachfolgend siehst du anhand des obigen Beispiels, wie eine Regression "entsteht":
Du hast einen positiven linearen Zusammenhang zwischen Freudfähigkeit und Humor festgestellt. Das würde bedeuten: je freudfähiger jemand ist, desto mehr Humor hat er oder sie – und umgekehrt: je humorvoller, desto freudfähiger. Oder: je weniger humorvoll, desto weniger freudfähig (und umgekehrt).
Beide metrische Variablen (Intervallskala) wurden auf einer Skala von 0 bis 100 erfasst, 0 = gar nicht vorhanden und 100 = extrem ausgeprägt.
Nun willst du untersuchen, ob bzw. wie du mit dem Humor die Freudfähigkeit vorhersagen kannst.
Wie oben bereits erwähnt, wird hier nicht auf die inferenzstatistische Auswertung eingegangen – das wäre dann die Beantwortung der Frage, ob der Humor ein signifikanter Prädiktor für die Freudfähigkeit ist. Wir beschäftigen uns hier einfach damit, ein Vorhersagemodell zu basteln, ohne auf statistische Signifikanz zu prüfen (das ist die deskriptivstatistische Auswertung).
1.
Linearer Zusammenhang zwischen beiden Variablen
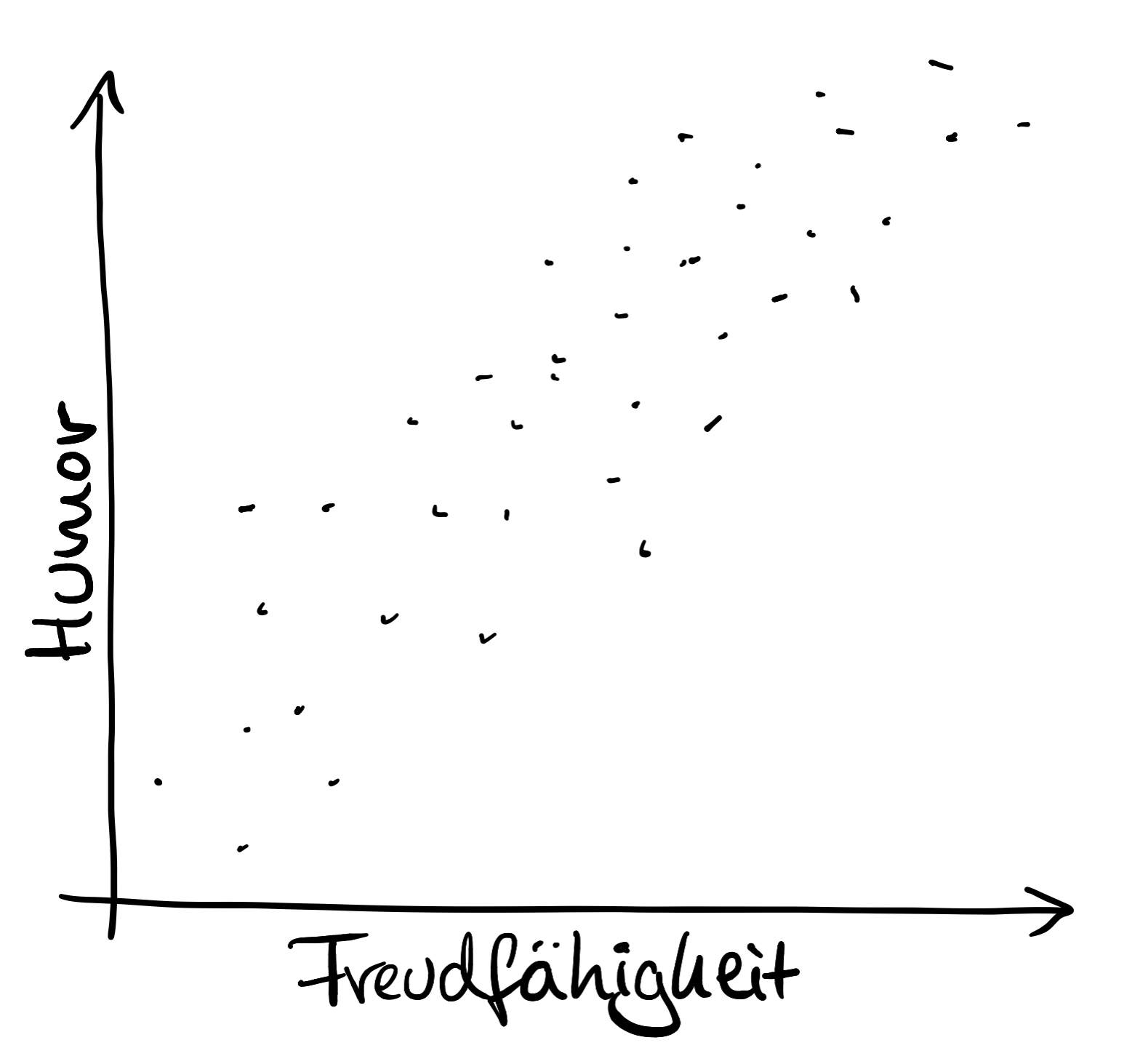
2.
Zuordnung: wer ist Prädiktor, wer Kriterium?
Meist ist es klar, welche Variable welche vorhersagt. Es gibt aber auch Fälle, wo das beliebig austauschbar ist.
Die vorhersagende Variable, der Prädiktor, wird nun auf die x-Achse gepackt, die vorhergesagte (Kriterium) auf die y-Achse.
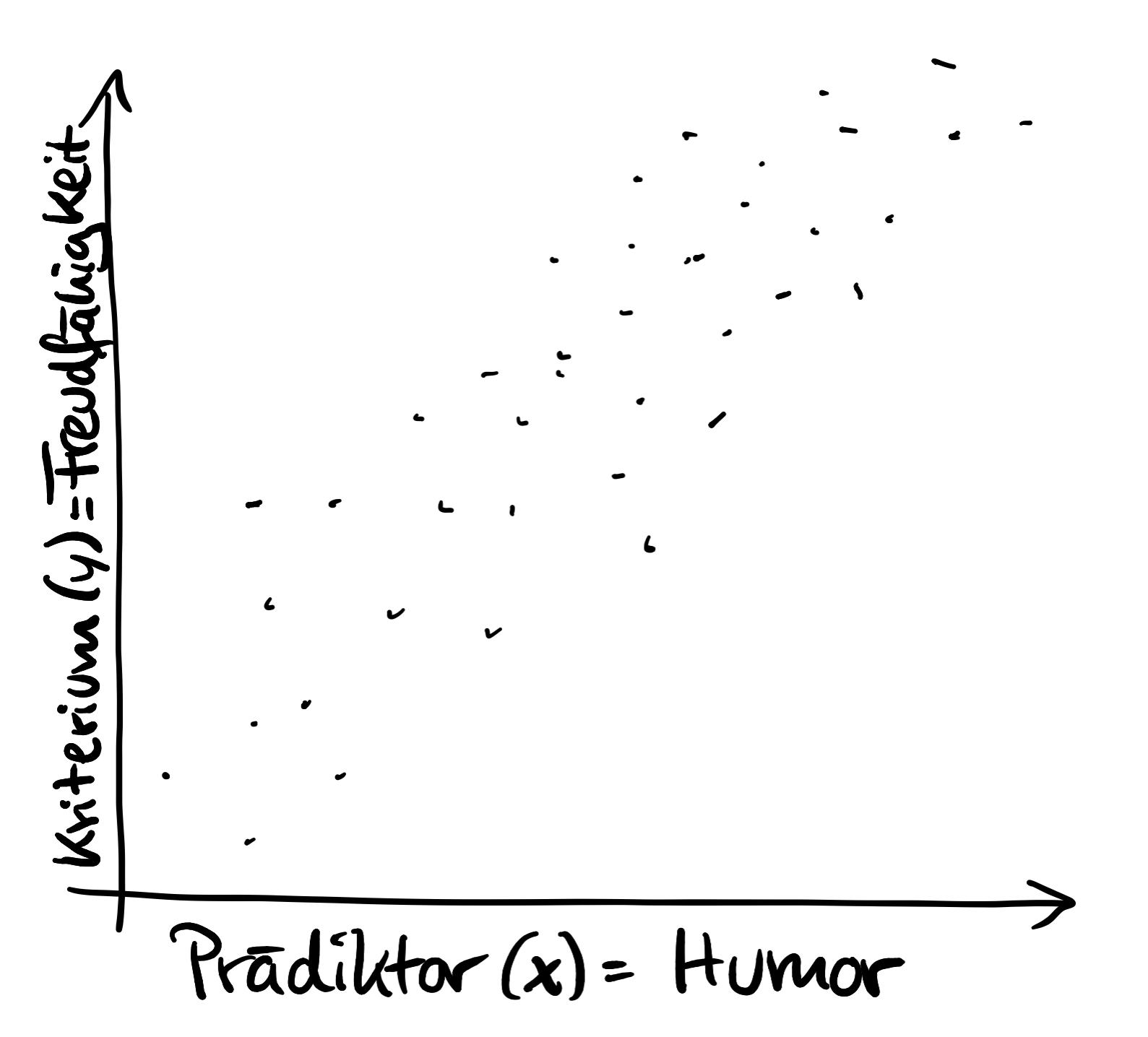
3.
Gerade finden, zu der die Abstände der Punkte am geringsten sind
Um ein Regressions-Modell zur Vorhersage zu erhalten, nutzen wir die Daten der Stichprobe und suchen diejenige Gerade, die so in der Punktewolke liegt, dass die Abstände aller Datenpunkte zur Geraden am kleinsten sind. Weiter unten folgt die genauere Erklärung zu diesem Schritt.
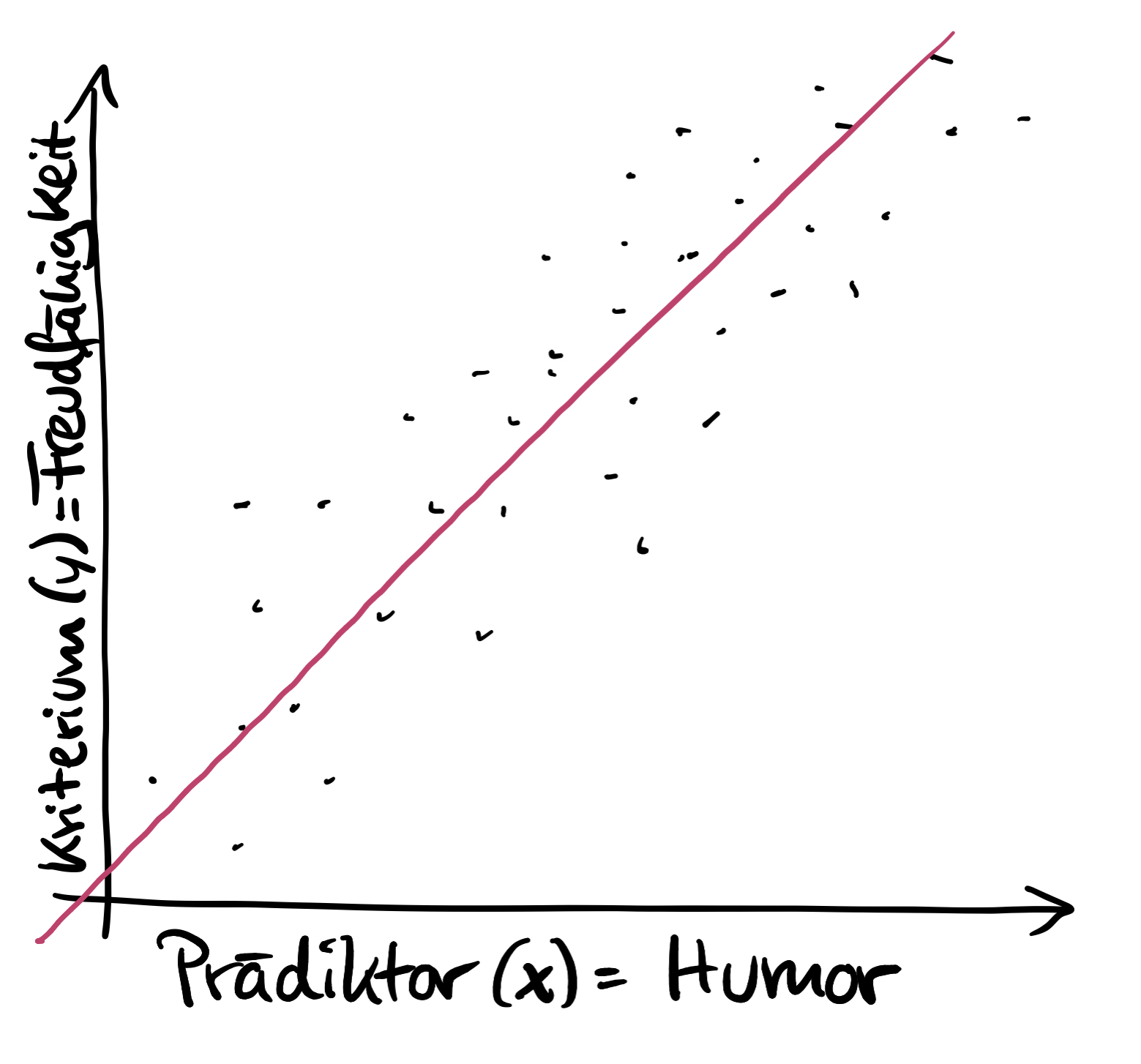
4.
Finales Modell – nur noch die Gerade!
Das ist der Schritt, der viele Studierende verwirrt: am Ende bleibt nur noch die Regressionsgerade übrig, die wir nun zur Vorhersage nutzen können. Wie das geht, zeige ich dir im Bild bei "5.".
Das bedeutet, dass wir die Daten aus der Stichprobe nur dazu verwenden, um die optimale Gerade (= optimales Vorhersagemodell) zu finden. Sobald wir die Gerade haben, interessieren uns die ursprünglichen Datenpunkte nicht mehr!
Übrigens: Die Regressionsgerade verläuft immer durch den Mittelwert von x und y
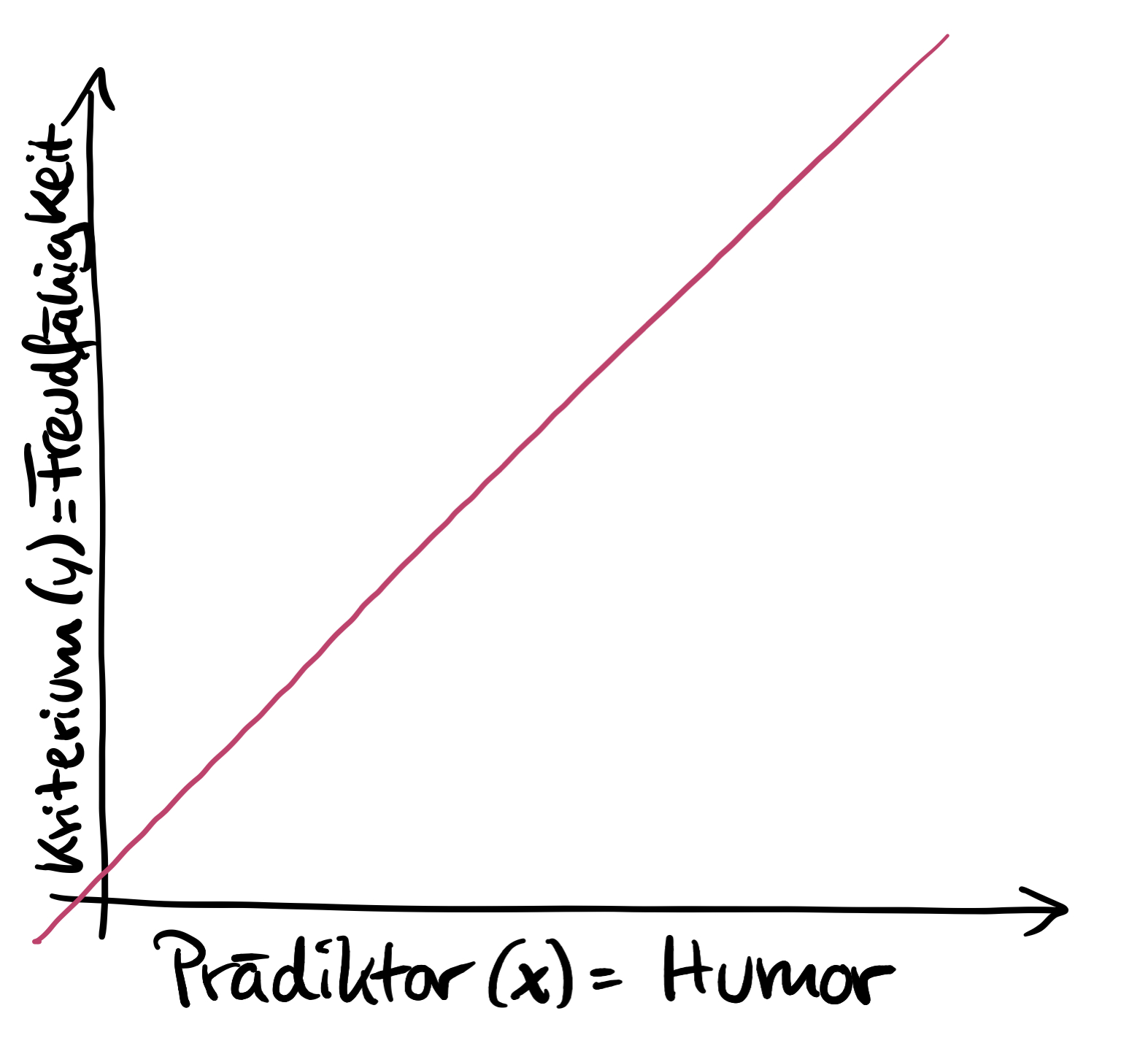
5.
Beispiel für die Vorhersage
Wenn du die Gerade hast, kannst du für jeden beliebigen Wert des Prädiktors den dazugehörigen Wert im Kriterium vorhersagen.
In unserem Beispiel könnten wir also ganz wild für jeden Humor-Wert zwischen 0 und 100 eine Vorhersage für den dazugehörigen Freudfähigkeitswert derselben Person treffen.
Im "echten Leben" wird das natürlich alles berechnet. Ich zeige dir das jetzt erst einmal zum besseren Verständnis nur grafisch, bevor wir uns anschließend beherzt in die Berechnung stürzen.
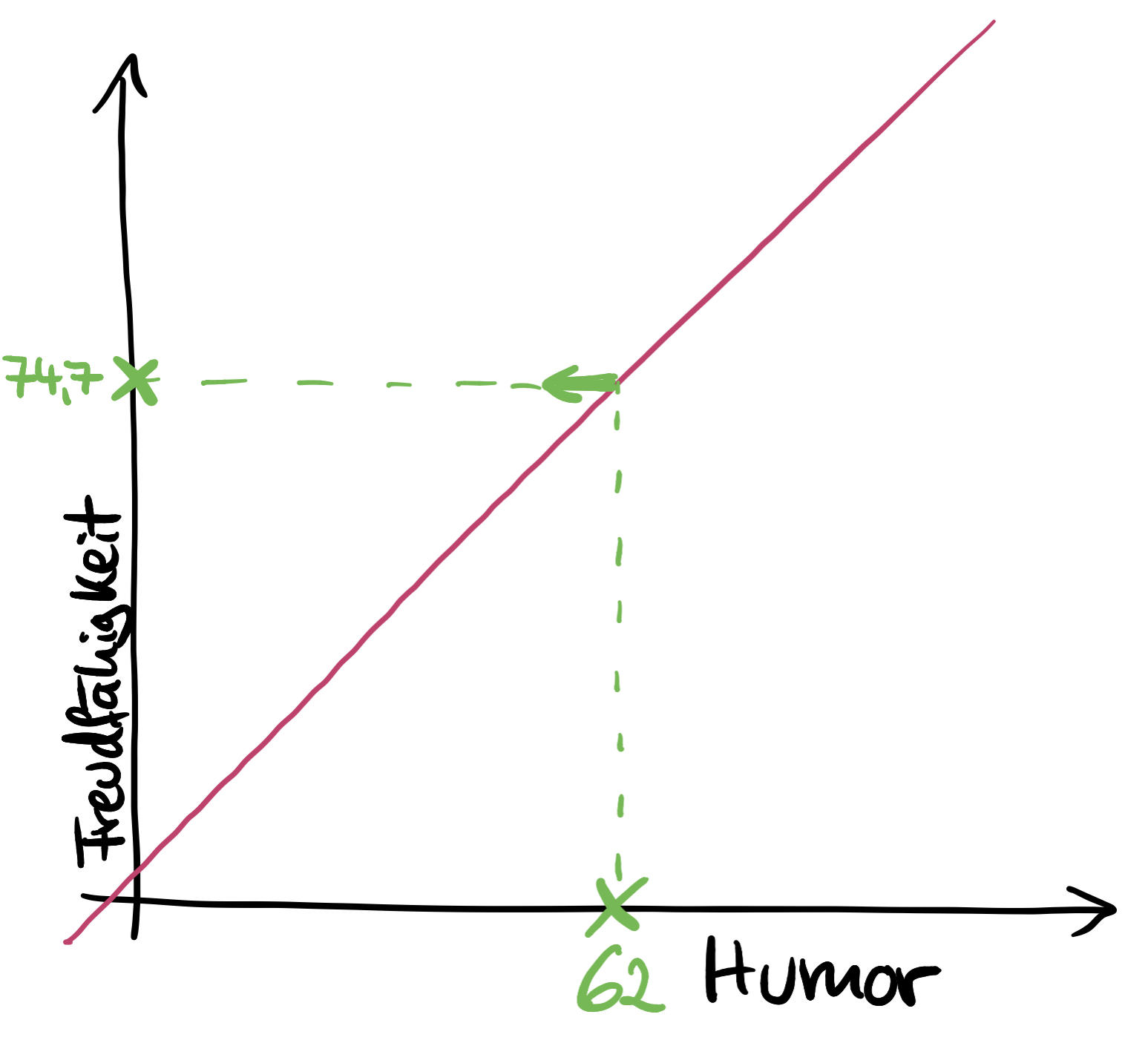
Was wir nun wissen wollen, ist, welcher Freudfähigkeits-Wert für jemanden mit einem leicht überdurchschnittlich ausgeprägten Humor (Wert von 62) vorhergesagt wird.
Dazu geht man auf der x-Achse bei 62 senkrecht nach oben, bis man die Gerade erreicht.
Hier macht man eine harte Linkskurve, wandert waagrecht bis zur y-Achse und liest dort den Wert ab. Das ist der vorhergesagte Freudfähigkeits-Wert – hier: 74,7, also ziemlich freudfähig (bei der Interpretation immer die dazugehörige Skala im Auge haben!).
Guckst du:

brauchst du hilfe beim lernen von statistik?
Dann komm' zu Statistik-gym, dem Online-Fitnessstudio für Statistik,
das dich fit für die Prüfung macht!
Eine Mitgliedschaft wie bei Netflix oder Spotify, nur eben für Statistik im Bachelor,
die dir hilft, dieses Fach endlich zu verstehen & die Prüfung zu meistern!
Darin bekommst du:
Und dann macht Statistik vielleicht sogar Spaß!
Klingt gut? Dann klick' hier:
Wie findet man die optimale Gerade?
Die KQ-Schätzung
Die optimale Gerade liegt so in der Punktewolke, dass die Abstände zwischen den Datenpunkten aus der Stichprobe zur Geraden am kleinsten sind – parallel zur y-Achse, nicht im Lot zur Geraden!
Diese Abstände heißen Residuen (Einzahl: Residuum) oder auch Vorhersagefehler. Meist werden sie als "e" für "error" bezeichnet.
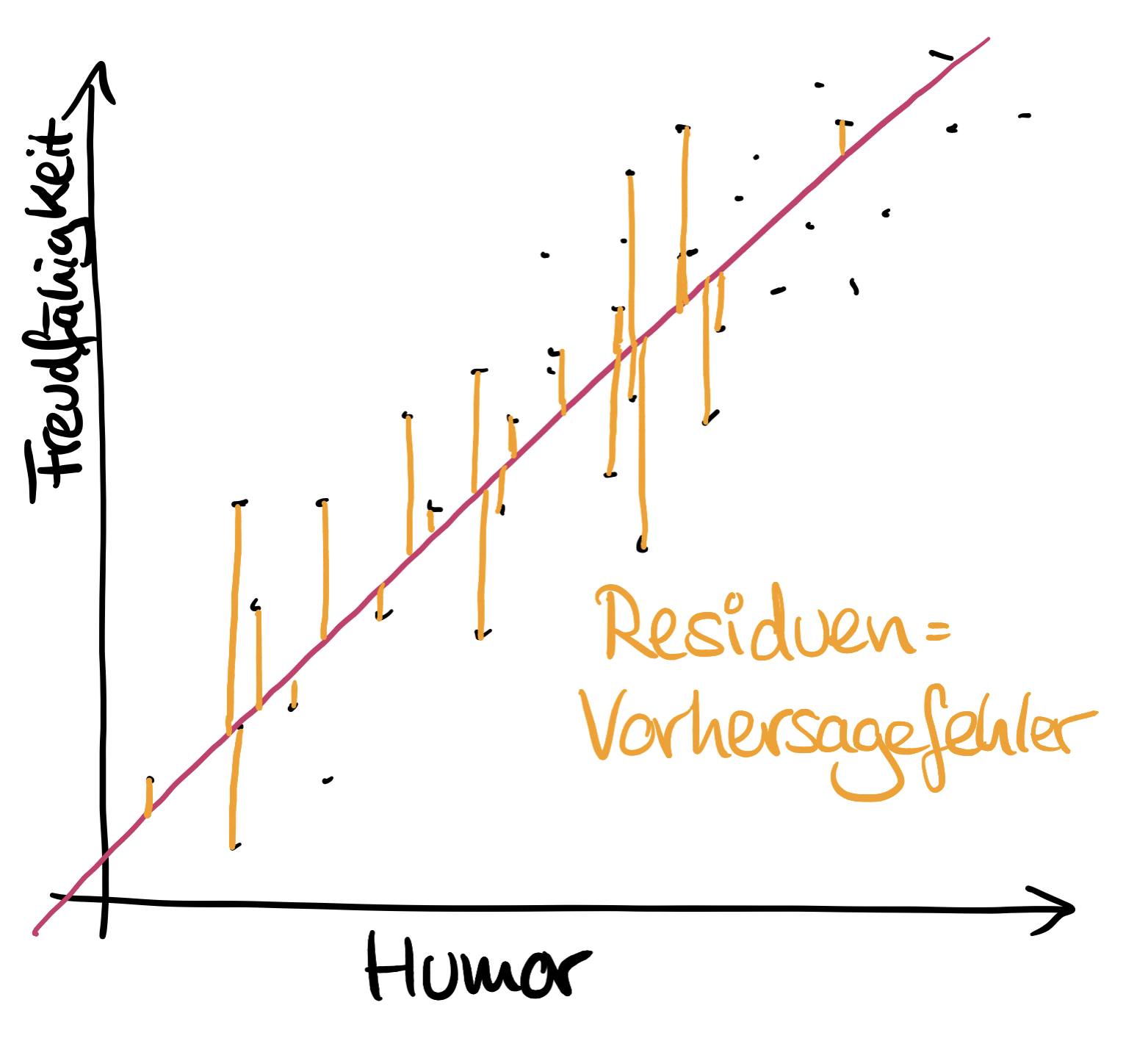
Der Punkt, wo das Residuum auf der Geraden auftrifft, ist der vorhergesagte Wert, meist als "y Dach" bezeichnet, mit einem schicken Häubchen drauf. Nähere Erklärung siehe unten bei den verschiedenen Bezeichnungen.
Der Datenpunkt aus der Stichprobe ist y.
Die Residuen werden berechnet, indem man vom Wert von y den vorhergesagten Wert y Dach abzieht – siehe Grafik.

Die Residuen / Abstände zur Geraden sind oberhalb der Geraden positiv und unterhalb negativ und summieren sich immer zu 0 auf. Daher hinter die feinen Löffelchen schreiben:
Die Summe der Residuen ist stets 0!
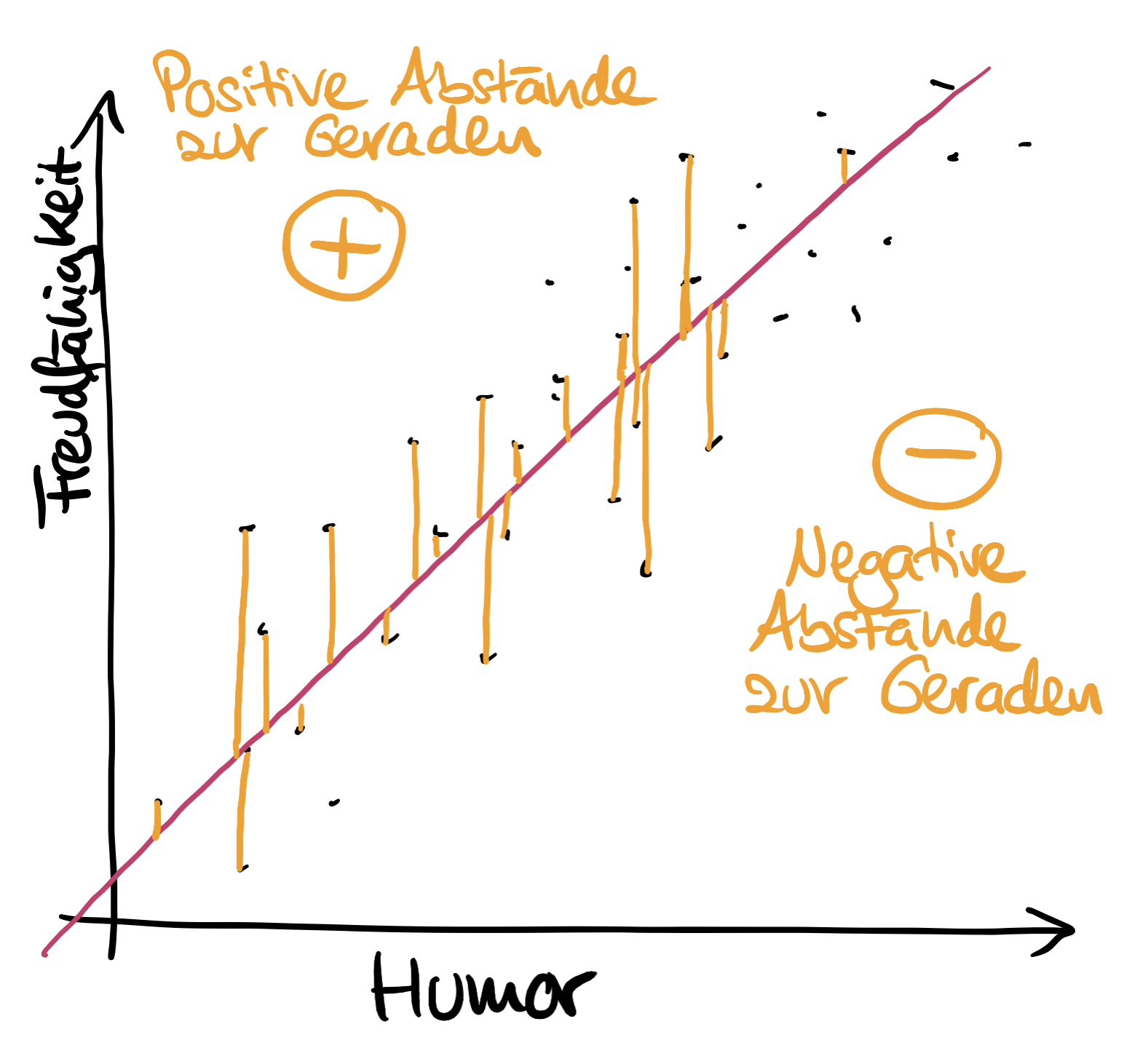
Nun will man aber genau diese Abstände verwenden, um die optimale Gerade zu finden.
Daher macht man etwas ganz Schlaues: man zählt die Residuen nicht einfach nur zusammen, denn das würde ja 0 ergeben, sondern quadriert alle Residuen, bevor man sie zusammenzählt. Dadurch wird das negative Vorzeichen entfernt und man erhält immer einen positiven Wert!
Jetzt schaut man, wo die Gerade liegen muss, damit dieser Wert am kleinsten ist (das wird von den Statistik-Programmen mit der sogenannten Differentialrechnung gemacht, was wir hier gar nicht so genau wissen wollen...).
Dieses Vorgehen ist die sogenannte "Kleinste-Quadrate-Schätzung" – oder für die Eingeweihten: "KQ-Schätzung" oder auch "Kriterium der kleinsten Quadrate".
Kleinste: wo sind die quadrierten zusammengezählten Residuen am kleinsten?
Quadrate: die Residuen werden alle erst ins Quadrat gesetzt und dann aufsummiert
Schätzung: wir können immer (bzw. in den allermeisten Fällen) nur von den Daten einer Stichprobe ausgehen, daher ist es eine Schätzung
Generell gilt: je kleiner die Residuen sind, desto besser oder genauer ist die Vorhersage! Je größer, desto schlechter bzw. ungenauer.
Ergebnis der KQ-Schätzung:
Mit der KQ-Schätzung erhält man die beiden Faktoren bzw. Koeffizienten, die die Lage der Regressionsgerade bestimmen, nämlich die sogenannten Regressionskoeffizienten a und b:
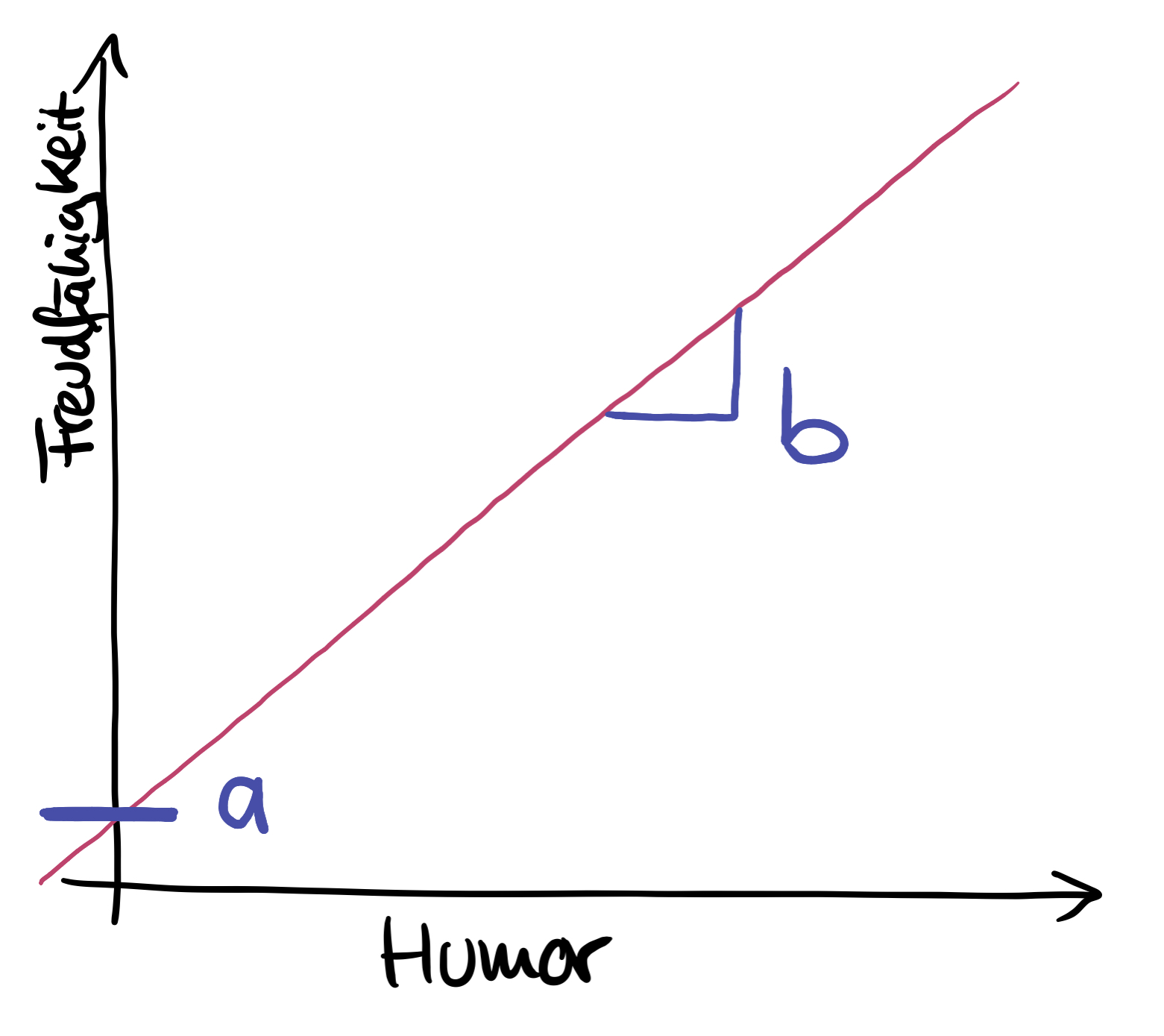
a oder Achsen-Abschnitt a oder die "Konstante": Wo schneidet die Gerade die y-Achse? Inhaltlich wird a meist nicht interpretiert, würde aber den vorhergesagten Wert von y bedeuten, wenn x = 0 wäre.
b oder die Steigung oder Regressionsgewicht: Wie steil ist die Gerade? b zeigt gewissermaßen den "Effekt" des Prädiktors auf das Kriterium, wobei man das nicht kausal verstehen darf!
Das Regressionsmodell bzw. die Regressionsgleichung heißt dann:
y = a + bx
Der vorhergesagte Wert setzt sich also zusammen aus: a + b mal x.
Achtung: b kann auch negativ sein! Dann würde die Gleichung heißen: y = a - bx
Hier siehst du a und b:
Berechnung von a & b
a und b können auch ohne die Differentialrechnung mit den folgenden Formeln berechnet werden:
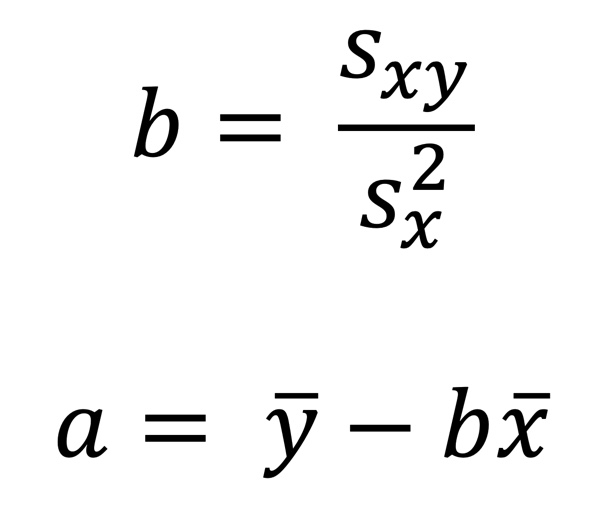
1. Schritt:
Kovarianz und Varianz von x berechnen (die Erklärung zur Berechnung der Varianz findest du hier). Das beinhaltet bereits das Berechnen der Mittelwerte von x und y.
2. Schritt:
b wird berechnet, indem man die Kovarianz durch die Varianz von x teilt.
3. Schritt:
a aus den zuvor errechneten Werten berechnen.
Praktische Vorhersage &
inhaltliche Bedeutung von a & b
Kommen wir zurück zu unserem Beispiel.
Angenommen, es wäre bei der Berechnung Folgendes herausgekommen:
a = 0.3 und b = 1.2
Dann heißt die Regressionsgleichung:
y = 0.3 + 1.2x
In der oberen Grafik wollten wir für einen Humor-Wert von 62 den vorhergesagten Freudfähigkeits-Wert wissen und haben das grafisch gemacht.
in "real life" macht man das jedoch mit der Gleichung, indem man für x den Wert 62 einsetzt:
y = 0.3 + 1.2 x 62 = 74.7
Dies kann man nun mit jedem beliebigen Humor-Wert tun und erhält dann jeweils den vorhergesagten Wert für die Freudfähigkeit.
Inhaltliche Bedeutung von a & b
Achsenabschnit a: wird wie erwähnt normalerweise nicht interpretiert und stellt die Vorhersage des Kriteriums bei einem Wert des Prädiktors von 0 dar.
WÖLLTEN wir das interpretieren, würde man Folgendes sagen: Wenn jemand absolut keinen Humor hat (Humor-Wert von 0), wird eine Freudfähigkeit von 0.3 vorhergesagt (also eher im sehr freudlosen Bereich).
Regressionsgewicht b: zeigt den "Effekt" des Prädiktors auf das Kriterium. Dabei gilt Folgendes:
Wenn x um eine Einheit ansteigt, verändert sich y um den Betrag b.
Praktisch bedeutet das:
Wenn der Humor-Wert um einen Punkt (das ist hier unsere Einheit) ansteigt, verändert sich y, d. h. der Wert der Freudfähigkeit, um 1.2. Hier ein paar Beispiel-Rechnungen:
y = 0.3 + 1.2 x 62 = 74.7
y = 0.3 + 1.2 x 63 = 75.9
y = 0.3 + 1.2 x 64 = 77.1
Wie du siehst, ist die Differenz zwischen den einzelnen Ergebnissen immer 1.2, was b entspricht. Ist b positiv, steigt y an; ist b negativ, verringert sich der Wert von y.
Wie sag' ich's Tante Erna?

Stell' dir vor, du bist bei deiner Tante Erna zu Schwarzwälder Kirschtorte und ordentlich Kaffee eingeladen. Tante Erna ist nicht die allerfirmste in Statistik, aber stets super interessiert an allem, was du so erhebst.
Also musst du ihr deine Ergebnisse in lai*innen-verständlicher Form nahebringen.
Das sähe hier so aus:
"Wir haben untersucht, ob man die Freudfähigkeit eines Menschen vorhersagen kann, wenn man weiß, wie humorvoll der- bzw. diejenige ist. Mit jedem bisschen, d. h. mit jedem Punkt mehr an Humor, steigt die Freudfähigkeit an, sogar um 1.2 Punkte. Wir haben aber noch nicht überprüft, ob dieses Ergebnis auch statistisch signifikant ist."
Mehr lässt sich ohne die Maße für die Qualität der Vorhersage und die weitergehende inferenzstatistische Auswertung nicht sagen.
Wie gut ist die Vorhersage?
Natürlich möchten wir auch noch wissen, wie gut die Vorhersage denn wirklich ist.
Hierfür gibt es zwei verschiedene Maße:
- R-Quadrat, auch Bestimmtheitsmaß oder Determinationskoeffizient genannt
- Standardschätzfehler
Du möchtest wissen, was das ist? Leider muss ich dich in dieser vermutlich nahezu unerträglichen Spannung lassen, denn beide Maße werden erst im nächsten Blog Post behandelt...
Verwirrung leicht gemacht! Die verschiedenen Bezeichnungen...
Wie du vermutlich schon leidvoll erfahren hast, gibt es in der Statistik zur allgemeinen Erbauung unterschiedliche Bezeichnungen für das Gleiche. Warum auch nicht!...
Hier ein Überblick:
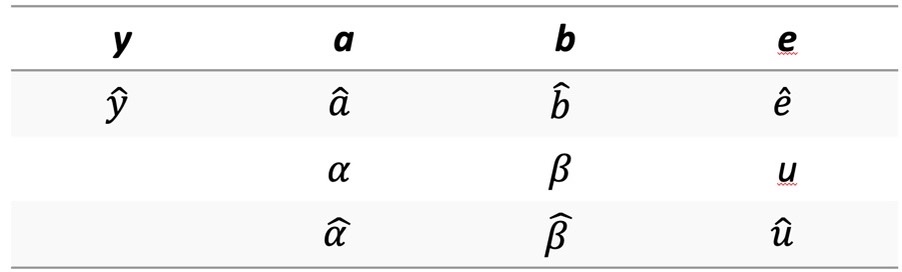
Das Häubchen / Hütchen in obiger Tabelle wird "Dach" genannt, also z. B. "alpha Dach".
Damit wird ausgedrückt, dass es sich nur um eine Schätzung und keinen definitiv "sicheren" Wert handelt, weil man ja meistens nur die Daten einer Stichprobe hat und damit auf alle für eine Fragestellung in Frage kommenden Personen schließen möchte.
Daher sind die resultierenden Werte immer nur eine Schätzung, basierend auf den erhobenen Daten der jeweiligen Stichprobe.
Zum Abschluss: Der Steckbrief zur Regression
Meine Challenge an dich
Um das Ganze ein wenig zu festigen, würde ich vorschlagen, dass du dir einen Übungs-Datensatz schnappst (oder dir selbst ein paar Werte überlegst) und gleich mal eine einfache Regression berechnest.
Viel Spaß und Erfolg!

QUELLEN (Als Amazon-Partnerin verdiene ich an qualifizierten Verkäufen):
Bortz, J., & Schuster, C. (2017). Statistik für Human- und Sozialwissenschaftler. Berlin: Springer.
Field, A. (2018). Discovering Statistics using IBM SPSS Statistics. London: SAGE.
KENNST DU SCHON MEINEN YOUTUBE-KANAL?

Guckst du hier: